「三平方の定理の利用」円錐の母線・正方形の対角線・三角形の高さ

中学３年生の数学で学習する「三平方の定理の利用」について、円錐の母線と正方形の対角線、三角形の高さを三平方の定理を使って求める方法をくわしく解説しているよ。

特別な直角三角形の３辺の比の関係についてもわかりやすく紹介するよ。

「三平方の定理の利用」 円錐の母線・正方形の対角線・三角形の高さのPDF（13枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 三平方の定理を利用して円錐の母線を求めよう
• 三平方の定理を利用して正方形の対角線を求めよう
• 三平方の定理を利用して正三角形の高さを求めよう
• 特別な直角三角形の３辺の比
• まとめ

三平方の定理を利用して円錐の母線を求めよう

三平方の定理を利用すると、円錐の母線を求めることができるよ。
三平方の定理を忘れてしまった人は再確認しておこうね。

直角三角形の３辺の長さをａ、ｂ、ｃとすると
ａ^２＋ｂ^２＝ｃ^２
という関係が成り立つよ。

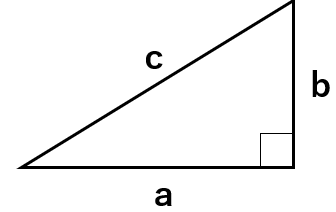
これを「三平方の定理」というんだったよね。

問題
下の図は、底面の半径が３cm、高さが４cmの円錐である。
母線の長さを求めなさい。

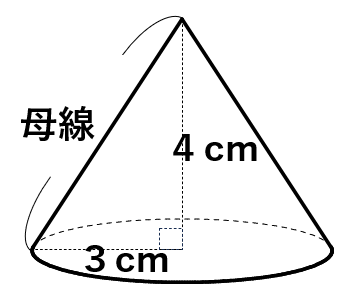
立体の問題は平面にして考えるとわかりやすいよ。
立体の円錐の、母線・高さ・底辺の半径部分に注目して平面で考えてみよう。

円錐の半径と高さは垂直に交わるから、次のような直角三角形を抜き出して考えることができるね。

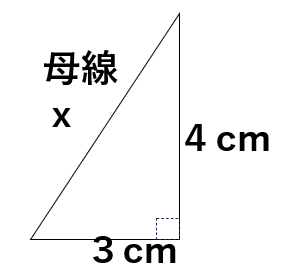
この直角三角形で三平方の定理を使うと
ａ^２＋ｂ^２＝ｃ^２
３^２＋４^２＝ｘ^２
９＋１６＝ｘ^２
２５＝ｘ^２
ｘ^２＝２５
ｘ＝±５

長さがマイナスはありえないから、母線の長さが５cmだとわかったね。

三平方の定理を利用して正方形の対角線を求めよう

それでは、三平方の定理を利用して、今度は正方形の対角線を求める方法を考えてみよう。

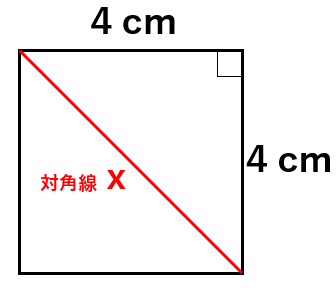
１辺が４cmの四角形の対角線の長さを求めなさい。

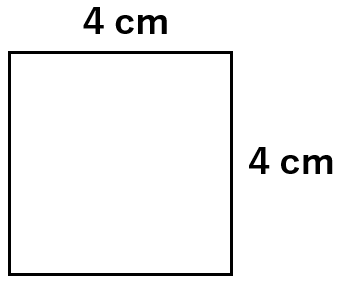
正方形の四隅の角度はすべて直角なので、対角線を引くと、直角三角形を作ることができるね。

この直角三角形で三平方の定理を使えば、対角線の長さを求めることができるんだ。

ａ^２＋ｂ^２＝ｃ^２
４^２＋４^２＝ｘ^２
１６＋１６＝ｘ^２
３２＝ｘ^２
ｘ^２＝３２
ｘ＝±\(\sqrt{３２}\)
ｘ＝±４\(\sqrt{２}\)

長さがマイナスはありえないから、対角線の長さが４\(\sqrt{２}\)cmだとわかったね。

三平方の定理を利用して正三角形の高さを求めよう

最後に、三平方の定理を利用して、正三角形の高さを求める方法を考えよう。

１辺が４ｃｍ正三角形の高さを求めなさい。

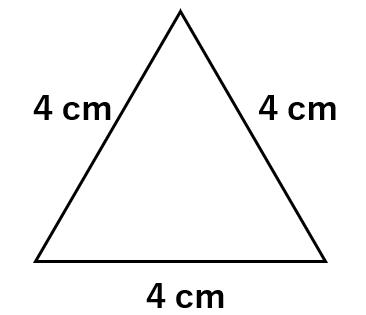
正三角形の頂点から底辺に垂線を引くと、底辺は垂直に２等分されるんだ。
なぜなら、二等辺三角形の定理「二等辺三角形の頂角の二等分線は、底辺を垂直に２等分する。」が使えるからだよ。

正三角形は、３辺が正しい三角形だよね。
ということは、もちろん「２辺が等しい」二等辺三角形の定理も使えるんだよ。※２辺が等しい三角形が、さらに３辺とも等しくなったのが正三角形だからね。

頂点から底辺に垂線を引くことで、底辺は垂直に２等分されて、直角を作り出すことができるし、２等分された底辺はそれぞれ２cmとなったね。

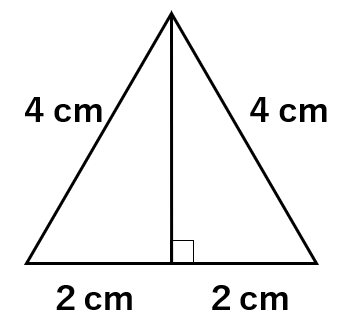
もとの１辺を斜辺とする直角三角形ができたね。

それでは色のついた直角三角形で三平方の定理を使おう。
※もちろん、左右どちらの直角三角形でも求めることができるよ。

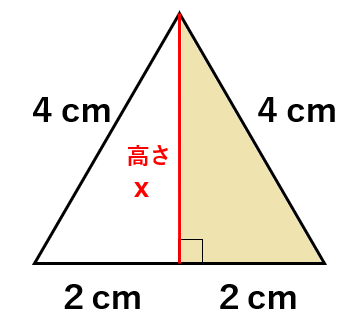
斜辺が４cmだから、ｃ＝４を代入しようね。

ａ^２＋ｂ^２＝ｃ^２
２^２＋ｘ^２＝４^２　　
４＋ｘ^２＝１６
ｘ^２＝１６－４
ｘ^２＝１２
ｘ＝±\(\sqrt{１２}\)
ｘ＝±２\(\sqrt{３}\)

長さがマイナスはありえないから、正三角形の高さが２\(\sqrt{３}\)cmだとわかったね。

特別な直角三角形の３辺の比

この「正方形の中にできる直角三角形」や「正三角形の中にできる直角三角形」は、「特別な直角三角形」と呼ばれるんだ。

なぜ特別扱いするかというと、この２つの直角三角形は、「３辺の比が決まっている」んだ。
だから、三平方の定理で二乗の計算を使わなくてもすぐに長さを求めることができる、便利な直角三角形なんだよ。

それでは、特別な直角三角形を２つ紹介するね。

45°、45°、90°の直角三角形

特別な直角三角形の１つ目は、３つの角が「４５°、４５°、９０°」の直角三角形。

さっき確認したとおり、正方形に対角線を引くと３つの角度が４５°、４５°、９０°の直角三角形ができたね。

「４５°、４５°、９０°」の３つの角度を見た瞬間、「よっしゃー」となる感じだよ。

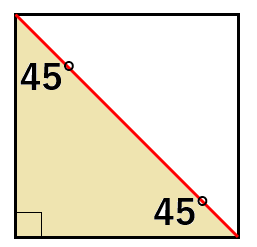
なぜ「よっしゃー」となるか説明をするね。

１辺の長さが２cmの正方形の対角線の長さ

たとえば、１辺の長さが２cmの正方形で対角線を求めてみるよ。

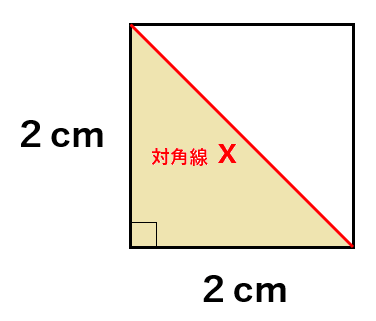
１辺の長さが２cmのときの対角線の長さは三平方の定理を使うと
ａ^２＋ｂ^２＝ｃ^２
２^２＋２^２＝ｘ^２
４＋４＝ｘ^２
８＝ｘ^２
ｘ^２＝８
ｘ＝±\(\sqrt{８}\)
ｘ＝±２\(\sqrt{２}\)

対角線の長さは２\(\sqrt{２}\)cmと求まるよ。

１辺の長さが３cmの正方形の対角線の長さ

では、今度は１辺の長さが３cmの正方形の対角線を求めてみるよ。

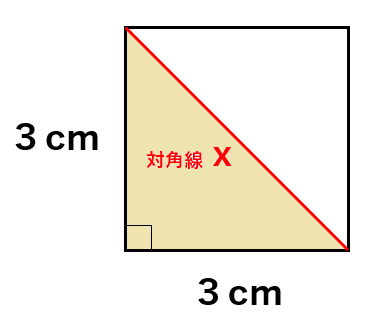
１辺の長さが３cmのときの対角線の長さは三平方の定理を使うと
ａ^２＋ｂ^２＝ｃ^２
３^２＋３^２＝ｘ^２
９＋９＝ｘ^２
１８＝ｘ^２
ｘ^２＝１８
ｘ＝±\(\sqrt{１８}\)
ｘ＝±３\(\sqrt{２}\)

対角線の長さは３\(\sqrt{２}\)cmと求まるよ。

１辺の長さが４cmの正方形の対角線の長さ

次に、１辺の長さが４cmの正方形の対角線を求めてみるよ。

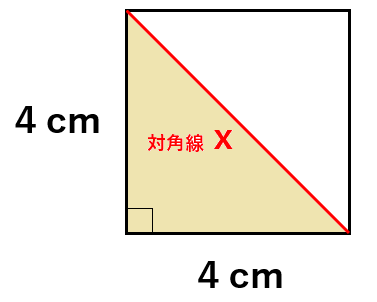
１辺の長さが４cmのときの対角線の長さは三平方の定理を使うと
ａ^２＋ｂ^２＝ｃ^２
４^２＋４^２＝ｘ^２
１６＋１６＝ｘ^２
３２＝ｘ^２
ｘ^２＝３２
ｘ＝±\(\sqrt{３２}\)
ｘ＝±４\(\sqrt{２}\)

対角線の長さは４\(\sqrt{２}\)cmと求まるよ。

45°、45°、90°の直角三角形の３辺の比

１辺の長さが２、３、４cmのそれぞれの場合の対角線の長さを求めたら、２\(\sqrt{２}\)、３\(\sqrt{２}\)、４\(\sqrt{２}\)cmになったよね。

下の図で再確認しよう。

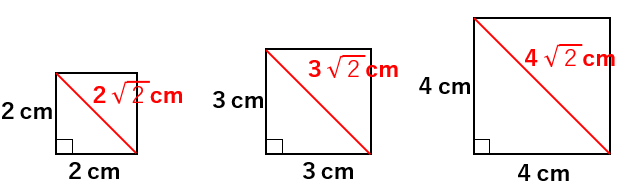
気が付くことがあるかな？

なんと４５°、４５°、９０°の直角三角形の３辺の比はすべて「１：１：\(\sqrt{２}\)」になっているんだ。

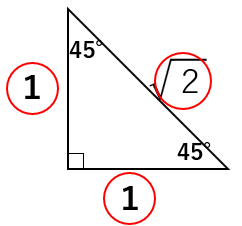
このとき、斜辺が\(\sqrt{２}\)になるというのがポイントだからおさえておこうね。

３つの角が「４５°、４５°、９０°」の直角三角形であれば、１辺の長さが分かれば他の長さもすぐに求めることができるということだね。

30°、60°、90°の直角三角形

特別な直角三角形の２つ目は「３０°、６０°、９０°」の直角三角形。

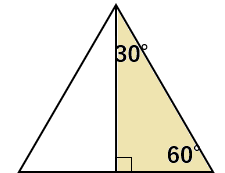
さっき確認したとおり、正三角形の頂点から垂線を引くと、３つの角度が「３０°、６０°、９０°」の直角三角形ができるよね。
※正三角形の角度はすべて６０°だからね。

１辺の長さが２cmの正三角形からできる直角三角形の３辺の長さ

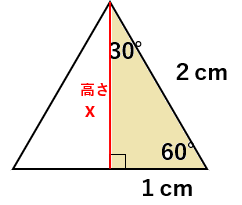
１辺の長さが２cmのときの正三角形の高さは三平方の定理を使うと
ａ^２＋ｂ^２＝ｃ^２
１^２＋ｘ^２＝２^２
１＋ｘ^２＝４
ｘ^２＝４－１
ｘ^２＝３
ｘ＝±\(\sqrt{３}\)

高さは\(\sqrt{３}\)cmと求まるよ。

１辺の長さが４cmの正三角形からできる直角三角形の３辺の長さ

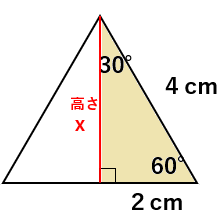
１辺の長さが４cmのときの正三角形の高さは三平方の定理を使うと
ａ^２＋ｂ^２＝ｃ^２
２^２＋ｘ^２＝４^２
４＋ｘ^２＝１６
ｘ^２＝１６－４
ｘ^２＝１２
ｘ＝±２\(\sqrt{３}\)

高さは２\(\sqrt{３}\)cmと求まるよ。

１辺の長さが６cmの正三角形からできる直角三角形の３辺の長さ

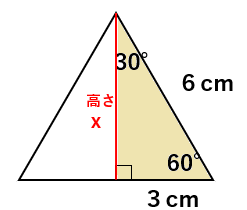
１辺の長さが６cmのときの正三角形の高さは三平方の定理を使うと
ａ^２＋ｂ^２＝ｃ^２
３^２＋ｘ^２＝６^２
９＋ｘ^２＝３６
ｘ^２＝３６－９
ｘ^２＝２７
ｘ＝±３\(\sqrt{３}\)

高さは３\(\sqrt{３}\)cmと求まるよ。

30°、60°、90°の直角三角形の３辺の比

１辺の長さが２、４、６cmの正三角形それぞれの場合、高さを求めたら、\(\sqrt{３}\)、２\(\sqrt{３}\)、３\(\sqrt{３}\)cmになったよね。

下の図で再確認してみよう。

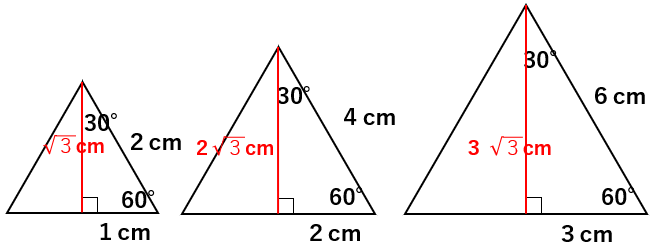
今度も気が付くことがあるかな？

３０°、６０°、９０°の直角三角形の３辺の比はすべて「１：\(\sqrt{３}\)：２」になるんだ。

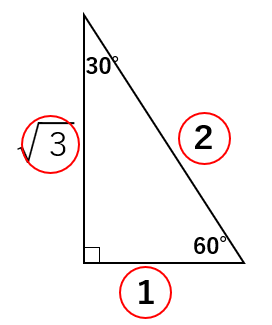
この直角三角形の場合、斜辺が「２」になるということがポイントなので、おさえておこう。

３つの角が「３０°、６０°、９０°」の直角三角形であれば、１辺の長さが分かれば、他の長さもすぐに求めることができるというわけだね。

「三平方の定理の利用」まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。