三平方の定理とは?公式の証明と問題の解き方をわかりやすく解説
中学3年生の数学で学習する「三平方の定理(ピタゴラスの定理)」の公式について、どうしてその公式・定理が成り立つのかを証明する方法をくわしく解説するよ。
三平方の定理を使った問題の解き方もていねいに紹介しているよ。
直角三角形の3辺の長さについて成り立つ関係の証明
直角三角形の3辺の長さには大切な関係があるんだ。
どんな関係があるかを確かめていこう。
確かめる方法はたくさんあるんだけど3つだけ紹介するね。
直角三角形の3辺の長さについて成り立つ関係の証明①
次のような直角三角形があったとしよう。
わかりやすくするために線を引いているよ。
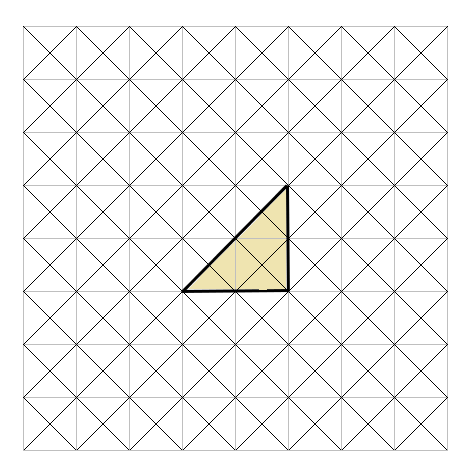
ここで、直角三角形の3つの辺を1辺とする正方形を作っていこう。
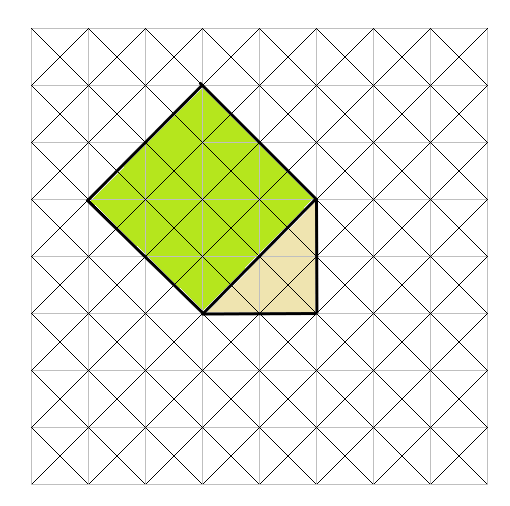
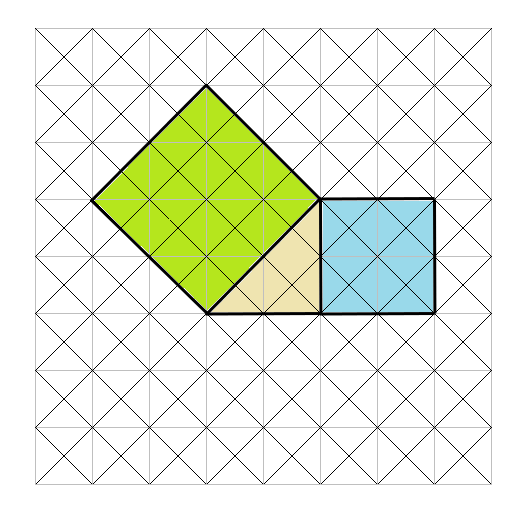
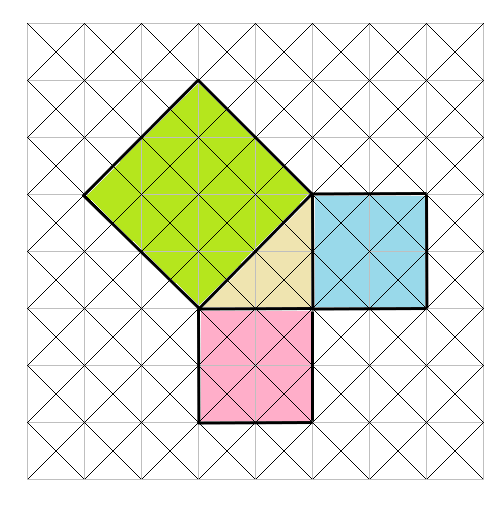
「直角三角形の周りにできた3つの正方形」は小さい三角形が何こ分かを数えると次の通りになるよ。
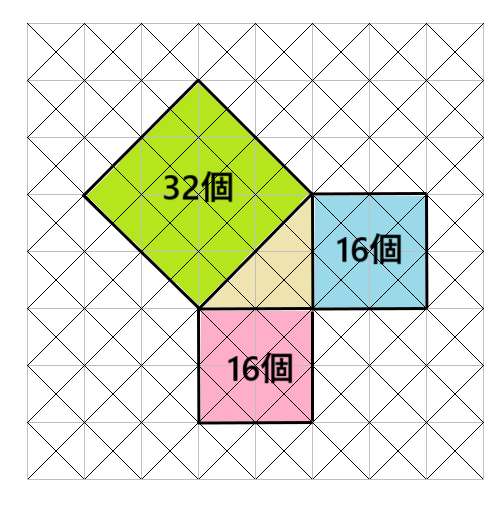
赤の正方形・・・16個
青の正方形・・・16個
緑の正方形・・・32個
→赤の正方形+青の正方形=緑の正方形になっていることがわかるね。
では、直角三角形の3辺の長さがa、b、cだとしよう。
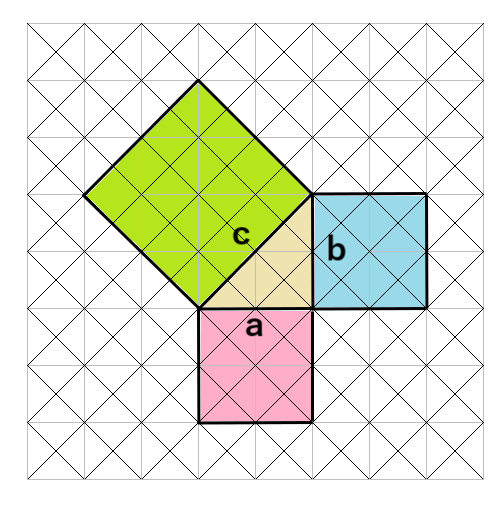
3つの正方形の面積は
赤の正方形・・・a2
青の正方形・・・b2
緑の正方形・・・c2
になるよね。
赤の正方形+青の正方形=緑の正方形だったから、
a2+b2=c2
という関係が成り立つね。
直角三角形の長さについて成り立つ関係を見つけられたね。
他の方法でも見つけてみよう。
直角三角形の3辺の長さについて成り立つ関係の証明②
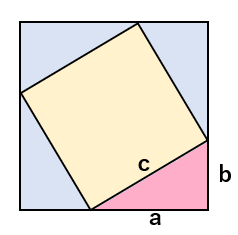
1辺が(a+b)の正方形と
1辺が c の正方形を使って考えていこう。
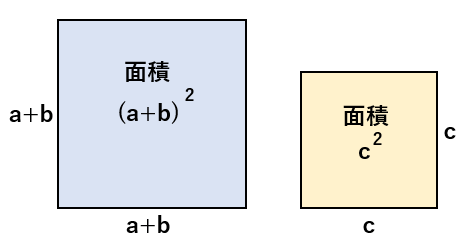
2つの正方形を次のように重ねてみたよ。
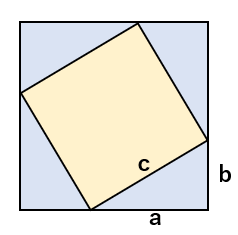
上の図からわかる面積
- 青の正方形全体の面積・・・(a+b)2
- 黄色の正方形の面積・・・c2
- 下に示した直角三角形1つ分の面積・・・a×b÷2=\(\frac{ab}{2}\)
これらの面積を使って、3辺の長さの関係を見つけよう。
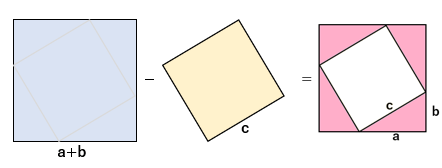
下の図の意味はわかるかな?
青の正方形から、黄色の正方形を引いたら、赤の直角三角形4こ分になることを表しているよ。
この関係を文字で表してみよう。
青の正方形-黄色の正方形=赤の直角三角形4こ分
(a+b)2-c2=\(\frac{ab}{2}\)×4 ←直角三角形4こ分だから「×4」
(a+b)2を展開して、\(\frac{ab}{2}\)×4を計算しよう。
(a+b)2-c2=\(\frac{ab}{2}\)×4
a2+2ab+b2-c2=2ab ←両辺に2abがあるから消えるよ。
a2+b2-c2=0 ←「-c2」を右辺に移項しよう。
a2+b2=c2
さっきと同じように
a2+b2=c2
という関係が導けたね。
最後にもう1つの方法でも証明してみよう。
直角三角形の3辺の長さについて成り立つ関係の証明③
合同な直角三角形を2つ組み合わせてみよう。
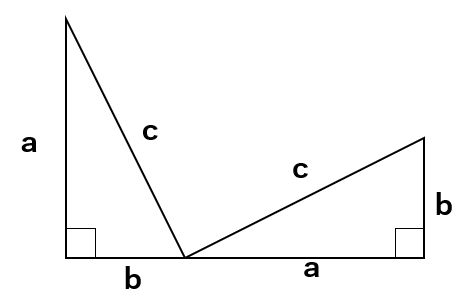
次のように線を引くと、新たに直角三角形が出来上がるよ。
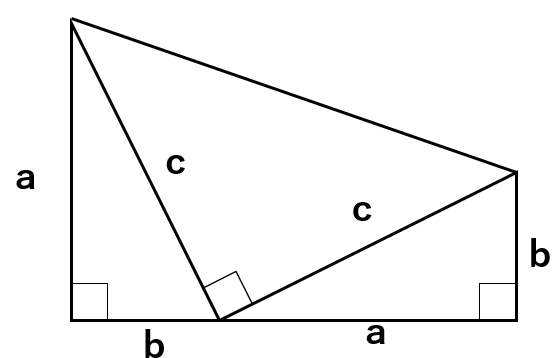
3つの三角形の面積と全体の台形の面積を求めよう。
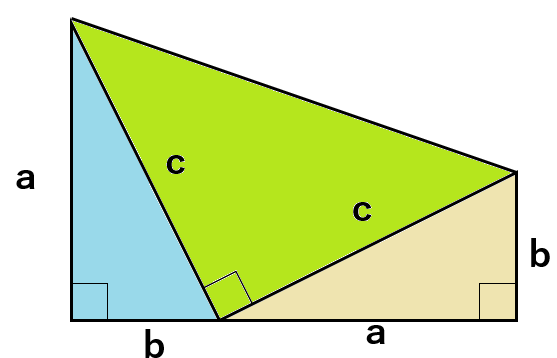
上の図からわかる面積
青の直角三角形と黄色の直角三角形の面積・・・a×b÷2=\(\frac{ab}{2}\)
緑の直角三角形の面積・・・c×c÷2=\(\frac{c^2}{2}\)
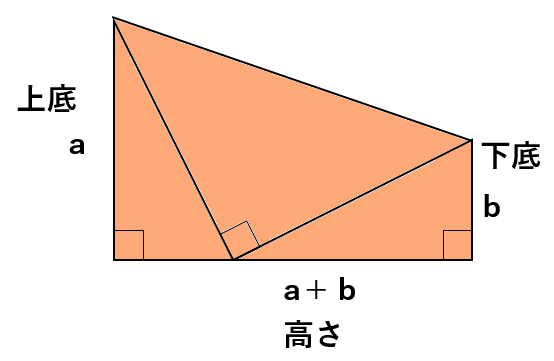
全体の台形の面積は下のように求められるよ
台形の面積の公式
(上底+下底)×高さ÷2
=(a+b)×(a+b)÷2
=(a+b)2÷2
=\(\frac{(a+b)^2}{2}\)
下の図の意味はわかるかな?
青の直角三角形と黄色の直角三角形と緑の直角三角形をたしたら、茶色の台形になることを表しているよ。
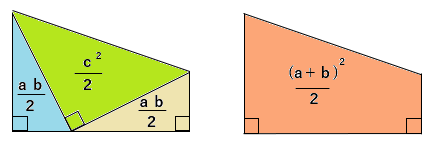
この関係を文字と式で表してみよう。
青の直角三角形+黄色の直角三角形+緑の直角三角形=茶色の台形 になるから、
\(\frac{ab}{2}\)+\(\frac{ab}{2}\)+\(\frac{c^2}{2}\)=\(\frac{(a+b)^2}{2}\)
すべて分母が2になっているから、両辺を2倍しよう。
\(\frac{ab}{2}\)×2+\(\frac{ab}{2}\)×2+\(\frac{c^2}{2}\)×2=\(\frac{(a+b)^2}{2}\)×2
ab+ab+c2=(a+b)2
(a+b)2を展開して式を整理しよう。
ab+ab+c2=(a+b)2
ab+ab+c2=a2+2ab+b2
2ab+c2=a2+2ab+b2 ←両辺に「2ab」があるから消すよ。
c2=a2+b2
さっきと同じように
a2+b2=c2
という関係が導けたね。
三平方の定理
直角三角形の3辺の長さについて成り立つ関係を3パターンで証明してきたね。
直角三角形の3辺の長さをa、b、cとすると
a2+b2=c2
という関係が成り立つよ。これを「三平方の定理」というんだ。
名前からしてなんとなくイメージできないかな?
「三」っていうのは、「3辺」のこと
「平方」っていうのは、「2乗」のこと
だから、3辺の2乗の性質ってことだね。
ちなみにだけど、「四平方の定理」っていうのもあるんだよ。
「四」だから、「4辺」になるんだよ。
イメージ 〇2=△2+◇2+▽2
三平方の定理
- 直角三角形の3辺の長さをa、b、cとすると
a2+b2=c2 - ギリシャの数学者ピタゴラスにちなんで、「ピタゴラスの定理」とも言われている(ピタゴラスが発見したかは定かではない)
三平方の定理を覚えることは簡単だよね。
テストでもこの定理を使った問題が出るので、次の練習問題にチャレンジしてできるようにしておこう。
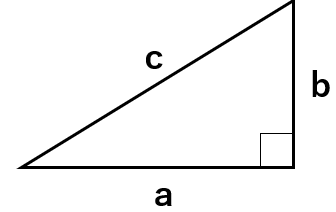
三平方の定理を使った問題
次の直角三角形でxの長さを求めなさい。
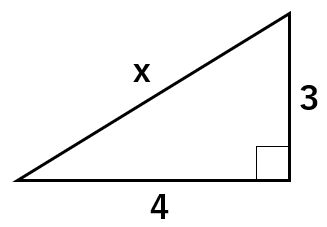
三平方の定理a2+b2=c2に数字や文字を当てはめて
42+32=x2
2乗の計算をしてxを求めよう。
42+32=x2
16+9=x2
25=x2
x2=25
x=-5、+5
長さにマイナスはないから、xの長さは5と求めることができるよ。
直角三角形の場合、2辺がわかったら残りの1辺が求められるというすごい性質なんだよ。
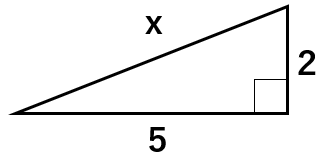
三平方の定理a2+b2=c2に数字や文字を当てはめて
52+22=x2
2乗の計算をしてxを求めよう。
52+22=x2
25+4=x2
29=x2
x2=29
2乗して29になる整数はないから、ルートを使って表そう。
x2=29
x=-\(\sqrt{29}\)、\(\sqrt{29}\)
長さにマイナスはないから、xの長さは\(\sqrt{29}\)と求めることができるよ。
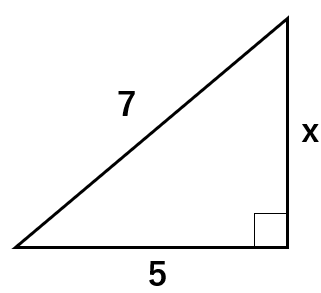
今までは斜辺がxだったんだけど、今度は違う辺がxになっているよ。ただやることは同じだよ。
三平方の定理a2+b2=c2に数字や文字を当てはめて
52+x2=72
2乗の計算をしてxを求めよう。
52+x2=72
25+x2=49
x2=49-25
x2=24
x=±\(\sqrt{24}\)
x=±2\(\sqrt{6}\)
長さにマイナスはないから、xの長さは2\(\sqrt{6}\)と求めることができるよ。
三平方の定理の問題の解き方
- 直角三角形の3辺の長さをa、b、cとして、
a2+b2=c2に当てはめる - cは直角三角形の斜辺になる
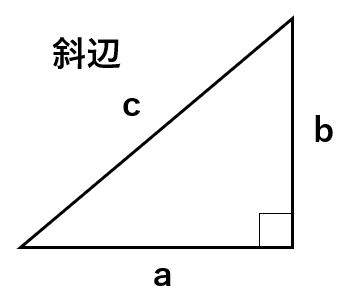
三平方の定理は直角三角形にしか使えないから、他の三角形で使ったりしないようにしようね。
三平方の定理(ピタゴラスの定理)まとめ
三平方の定理
- 直角三角形の3辺の長さをa、b、cとすると
a2+b2=c2 - ギリシャの数学者ピタゴラスにちなんで、「ピタゴラスの定理」とも言われている(ピタゴラスが発見したかは定かではない)
三平方の定理の問題の解き方
- 直角三角形の3辺の長さをa、b、cとして、
a2+b2=c2に当てはめる - cは直角三角形の斜辺になる

運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。

-
ゆみねこ先生ならではのご回答ありがとうございます。先生の書かれた証明の事も考えていたのでスッキリ納得出来ました。
質問を出させていただいたとき、画面の先頭に英文が表示され、説明文の画像が全て表示されていなかったのでなんか変だなと思ってました。サーバー容量の不足?? サイトの運営本当にご苦労様です。


すごくわかりやすい説明が入っていたりまとめもすっごくわかりやすかったです。
すごいです!