「標本調査」頻出の問題パターンは?応用問題の解き方を解説
中学3年生の数学で学習する「標本調査」について、定期テストや入試問題でよく出る頻出の問題パターンを紹介するよ。それぞれの問題・応用問題の解き方や考え方をくわしく解説するよ。
「標本調査」不良品の問題
例題
ある工場で作られた2万個のネジの中から200個を無作為に抽出して(ランダムに選んで)調べたところ、その中の4個が不良品でした。
ある工場で作られた2万個のネジには、およそ何個の不良品のネジが入っていると考えられますか。
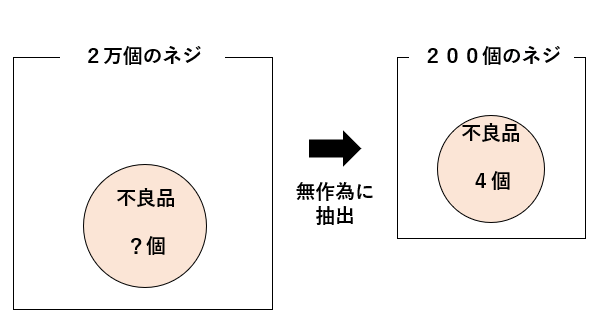
この問題の「母集団」「標本」が何かを確認しよう。
- 母集団:ある工場で作られた2万個のネジ
- 標本:選ばれた200個のネジ
2万個のネジをチェックするのって大変だよね。だから200個の標本を無作為に(ランダムに)抽出して、性能の確認をするんだよ。
では、実際に問題を解いていこう。
STEP1 不良品の割合を考える
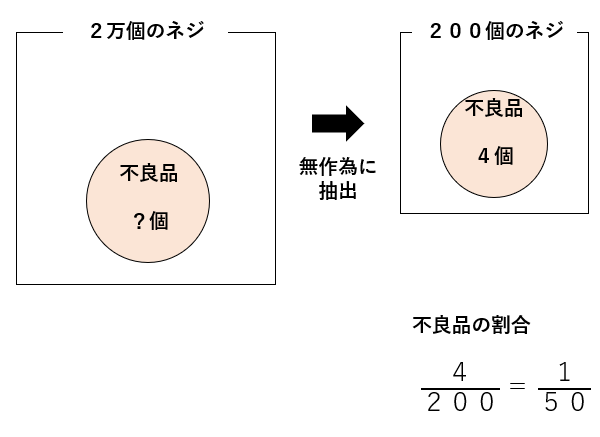
200個のうち、4個が不良品ということは、
不良品の割合は\(\frac{4}{200}\)=\(\frac{1}{50}\)
だね。
STEP2 2万個の不良品の数を推定する
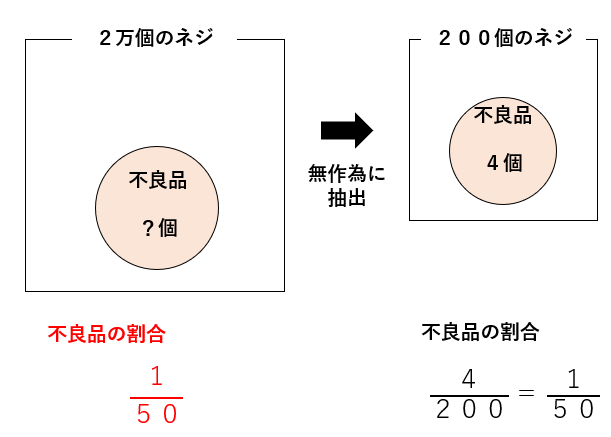
不良品の割合は\(\frac{1}{50}\)ということがわかっていたね。
標本調査の問題を解くときのポイントは〇〇の割合は等しくなると考えること。
今回の問題だったら不良品の割合は、200個の場合も2万個の場合も等しくなると考えて問題を解いていくよ。
2万個あったとしたら、
不良品の数は2万×\(\frac{1}{50}\)=400個と求めることができるよ。
なので、答えは
工場で作られた2万個のネジには、およそ400個の不良品のネジが入っていると考えられるよ。
「無作為に抽出する方法」について
今回の問題でも出てきた「無作為に抽出する方法」とはどういうものかを選ぶ問題などもよく出てくるよ。
例題
無作為に抽出する方法として、ふさわしいものを選びなさい。
- ア:乱数表を使って、製造番号で200個を選ぶ
- イ:最初に作った200個を選ぶ
- ウ:光っているネジを200個を選ぶ
- エ:最後に作った200個を選ぶ
答えは「ア」だよ。
「標本調査」の解説ページで、無作為に抽出する方法3つを紹介しているね。
そのうちのひとつが「ア」の「乱数表を使う方法」だったね。
イ・ウ・エは無作為に抽出したとは言わないよ。
「標本調査」それぞれの玉の数を求める問題
頻出問題
例題
白玉と赤玉が合わせて500個入った袋があります。
この袋の中から40個を無作為に取り出したところ、そのうちの10個が白玉でした。
袋の中には白玉が何個入っていると考えられますか。
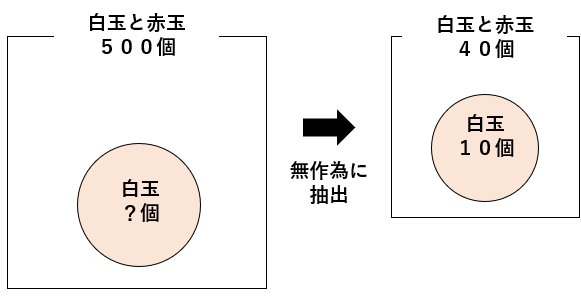
この問題の「母集団」「標本」が何かを確認しよう。
- 母集団:袋の中に入った、白玉と赤玉500個
- 標本:取り出した40個
500個の玉の色をチェックするのって大変だよね。だから40個の標本を無作為に(ランダムに)抽出して、色の確認をするんだよ。
では、実際に問題を解いていこう。
STEP1 白玉の割合を考える
40個のうち、10個が白玉ということは、
白玉の割合は\(\frac{10}{40}\)=\(\frac{1}{4}\)
だね。
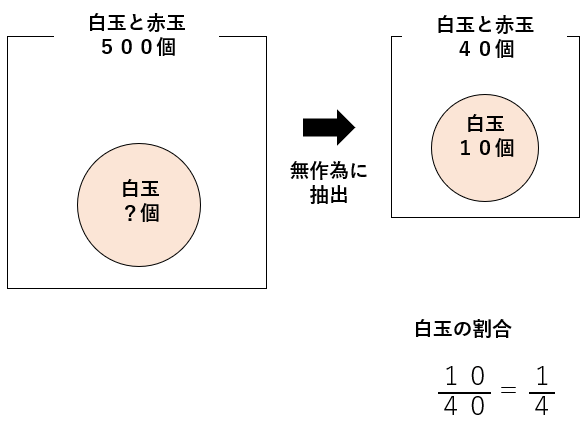
STEP2 500個の袋の中にある白玉の数を推定する
白玉の割合は\(\frac{1}{4}\)ということがわかっていたね。
標本調査の問題を解くときのポイントは〇〇の割合は等しくなると考えることだったよね。
今回の問題だったら白玉の割合は、40個の場合も500個の場合も等しくなると考えて問題を解いていくよ。
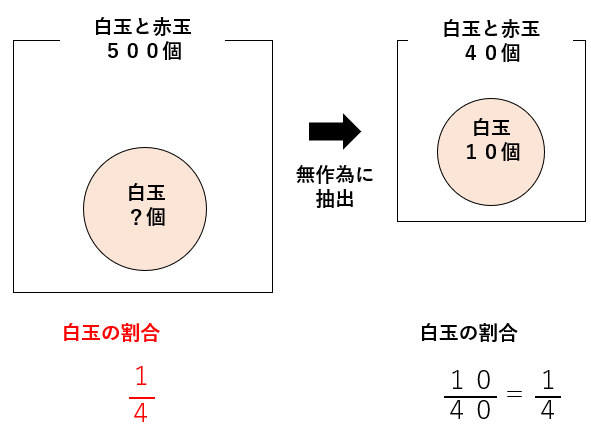
500個あったとしたら、
白玉の数は500×\(\frac{1}{4}\)=125個と求めることができるよ。
答えは
袋の中に入っている白玉と赤玉500個には、およそ125個の白玉が入っていると考えられるよ。
少し応用問題を紹介するね。
応用問題
例題
袋の中に白玉だけが入っています。多くて数えきれないので、赤玉200個を入れ、よくかき混ぜました。
その後50個の玉を無作為に抽出すると、赤玉が10個含まれていました。
はじめに袋の中に入っていた白玉の数は、およそ何個と考えられますか。
白玉が多すぎて数えるのが大変だから、赤玉200個を追加でいれるというのはなんともザンシンな方法だね。
問題のレベルも少しアップしているよ。
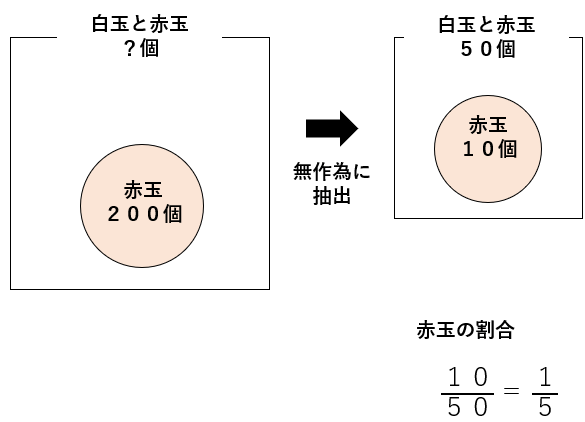
「袋の中に赤玉200個入れた後」の図は次のようになるよ。
もともとの白玉の数がわからないから、赤玉を入れた後もわからないよね。
図には「?個」と書いたよ。
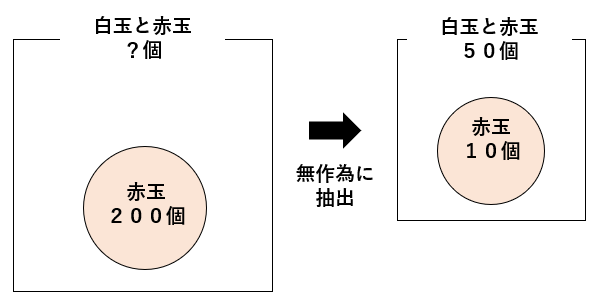
この図をもとに「はじめに袋の中に入っていた白玉の数」を求めよう。
STEP1 赤玉の割合を考える
50個のうち、10個が赤玉ということは、
赤玉の割合は\(\frac{10}{50}\)=\(\frac{1}{5}\)
だね。
STEP2 袋の中にある白玉と赤玉の数を推定する
赤玉の割合は\(\frac{1}{5}\)ということがわかっていたね。
標本調査の問題を解くときのポイントは〇〇の割合は等しくなると考えることだったよね。
今回の問題だったら赤玉の割合は等しくなると考えて問題を解いていくよ。
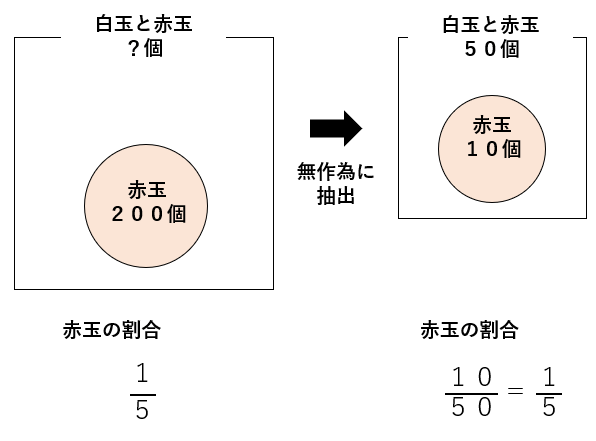
左の図で「?」を「x」としよう。
袋の中に入っている赤玉の数は次の式で求められるよ。
x×\(\frac{1}{5}\)=200
この式からxの値を求めると
x=200×5=1000個
袋の中に入っている白玉と赤玉の数は、およそ1000個と考えられるよ。
ただ、今回の問題でも求めるのは、「はじめに袋の中に入っていた白玉の数」だから、1000から「追加した赤玉200個」を引いて800個が答えになるよ。
「標本調査」魚の数を求める問題
例題
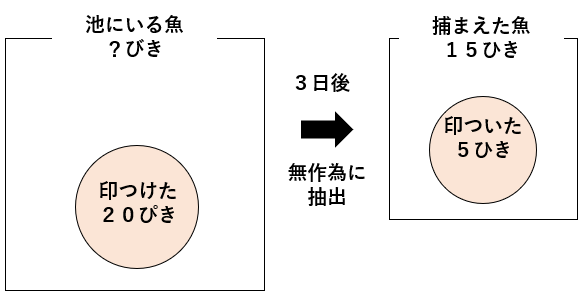
ある池の魚の数を調べるため、無作為に20ぴき捕まえ、その全部に印をつけて池に戻しました。
3日後、再び無作為に魚を15ひき捕まえると、印のついた魚が5ひきいました。
この池にいる魚の数を求めなさい。
この問題の「母集団」「標本」が何かを確認しよう。
- 母集団:池の中にいる魚(今回は数がわからないよ)
- 標本:3日後に捕まえた15ひきの魚
今回は全部の魚の数を求めるんだよ。
まさかすべての魚を池から取り出して数えるなんてしないよね。
だから標本調査で一部の魚だけを取り出しているよ。
では、実際に問題を解いていこう。
STEP1 印のついた魚の割合を考える
3日後に取り出した15ひきの魚のうち、5ひきに印がついているということは、
印のついた魚の割合は\(\frac{5}{15}\)=\(\frac{1}{3}\)
だね。
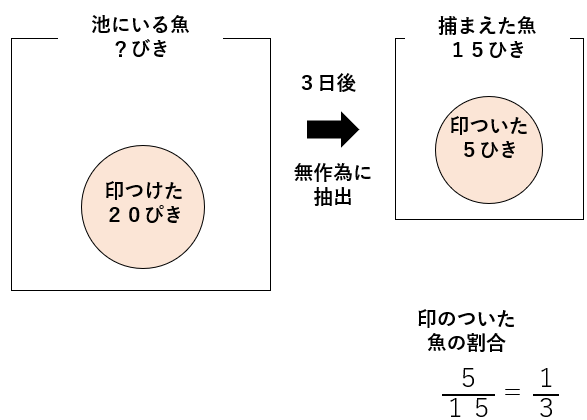
STEP2 池の中にいる魚の数を推定する
印のついた魚の割合は\(\frac{1}{3}\)ということがわかっていたね。
標本調査の問題を解くときのポイントは〇〇の割合は等しくなると考えることだったよね。
今回の問題だったら印のついた魚の割合は、「池の魚すべて」の場合も「取り出した15ひき」の場合も等しくなると考えて問題を解いていくよ。
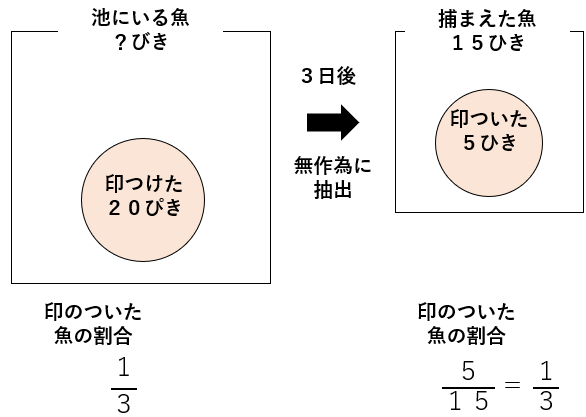
池にいる魚の数を求めたいから「xびき」としよう。
印のついた魚の数は次の式で求められるよ。
x×\(\frac{1}{3}\)=20
この式からxの値を求めると
x=20×3=60ぴき
答えは
池にいる魚の数は、およそ60ぴきと考えられるよ。
この問題では、つぎのようなことも聞かれる時があるよ。
例題
3日後に魚を捕まえた理由は何か。
なぜ3日も待たないといけないのだろうかと、問題を解いていて思った人はいないかな?
3日待つ理由は、
印がついた魚が十分に他の魚と混ざるからだよ。
もし、混ざっていなかったら、再び取り出すときに
- 印がついていない魚しか取れなかった
- 印がついている魚しか取れなかった
ということになるかもしれないからね。
「標本調査」は、どれだけ正確なデータを出せるようにするかが重要だということをおさえておこう!
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。