比例のグラフと表から比例の式を求めよう「比例式の求め方」を解説

中学１年生の数学で学習する「比例の式の求め方」について、比例のグラフやｘとｙが比例の関係を表す表から、比例の式を求める方法をわかりやすく解説しているよ。

比例のグラフと表から比例の式を求めよう 「比例式の求め方」を解説のPDF（8枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 表を使った比例の式の求め方
• 比例のグラフカラ式を求める方法

表を使った比例の式の求め方

比例の関係を表す表を使って、比例の式を求める方法の解説に入る前に、「比例」とはどういうものだったか、「比例の性質」の復習をしよう。

今回学習する「比例の関係を表す表から、比例の式を求める」ために使う比例の性質は、「ｙ＝ａｘ」という形で書くことができること。

では、実際に例題を見てみよう。

（例題）
次の表は比例の関係を表したものです。ｙをｘの式で表しなさい。

【求め方】

STEP１
問題文には「ｙをｘの式で表しなさい」と書かれているけれど、つまり簡単に言いかえると「ｙ＝○ｘ」になるか教えてね。という意味になるんだよ。

「ｙ＝○ｘ」の「○」に入る数がわかればOKなんだ。

STEP２
ではどうやって○の数を求めるかを考えよう。

「ｙ＝○ｘ」という言葉を直すと、
「ｙ」は「ｘ」を○倍した値という意味になるから、「ｘ」を何倍したら「ｙ」になっているかを確認しよう。
※ｙ÷ｘをすればいいね。

STEP３
表のｘとｙの値を確認すると、「ｘ」を２倍すると「ｙ」になっているね。

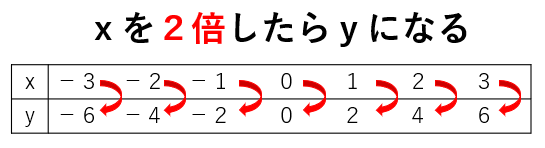
なので、〇には「２」が入って、ｙ＝２ｘがこの表の比例の式だと求まるよ。

たろう

比例の式ｙ＝ａｘを覚えていれば楽勝だね。

（例題）
次の表は比例の関係を表したものです。ｙをｘの式で表しなさい。

さっきと同じように考えていこう。

STEP１
比例だから「ｙ＝○ｘ」という形になるんだったよね。これは覚えておかないとね。

「ｙ＝○ｘ」の「○」に入る数がわかればOK。

STEP２
「ｙ＝○ｘ」という言葉を直すと、「ｙ」は「ｘ」を○倍した値という意味になるから、「ｘ」を何倍したら「ｙ」になるのかを確認しよう。

STEP３
表を見ると「ｘ」を－３倍したら「ｙ」になっているから、ｙ＝－３ｘが比例の式と求まるよ。

たろう

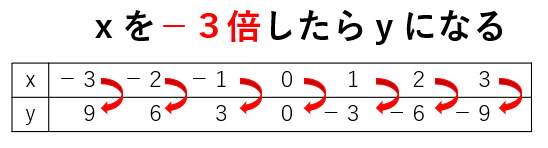
表がすべて埋まっていなくても、比例の式って求まりそう。

くまごろう

１つのｘの値とｙの値がわかれば、実は比例の式って求まるんだよ。例えば次の問題を考えよう。

表がなくても、無理やり表にしたら次のようになるよ。

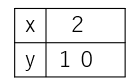
表にするまでもないけどね・・・。

STEP１
比例だから「ｙ＝○ｘ」という形になるんだったよね。

STEP２
「ｙ＝○ｘ」という言葉を直すと、「ｙ」は「ｘ」を○倍した値という意味になるね。

STEP３
表を見ると「ｘ」を５倍したら「ｙ」になっているから、ｙ＝５ｘが比例の式と求まるよ。

たろう

１つのｘの値とｙの値がわかれば、比例の式が求まるんだね。

くまごろう

実はこの問題ってよく入試問題に出るんだ！だからもう少し練習してみよう。

「比例」といったらｙ＝ａｘになることは絶対に覚えておこう。では実際に問題を考えよう。

（１）「ｘ」を３倍したら、「ｙ」になるから、ｙ＝３ｘ

（２）「ｘ」を５倍したら、「ｙ」になるから、ｙ＝５ｘ

（３）「ｘ」を３倍したら、「ｙ」になるから、ｙ＝３ｘ

「なんだ、簡単だよ」と思ったかもしれないけれど、このあと学習する「反比例」や２年生で学習する「一次関数」、３年生で学習する「二乗に比例する関数」とごちゃごちゃになって間違えやすい問題なんだ。

なので、ここでしっかりと押さえておこうね。

比例のグラフから式を求める方法

次に「比例のグラフから比例の式を求める」方法について考えていこう。
この方法でも、「比例の式はｙ＝ａｘで表される」という性質が重要になるよ。

さっそく問題を見てみよう。

（例題）

次のグラフはｙはｘに比例することを表している。
ｙをｘの式で表しなさい。

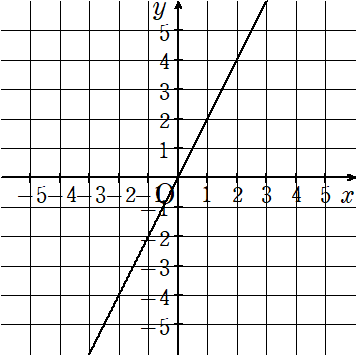
さっきの表から比例の式を求める方法とSTEP１までは一緒だよ。

STEP１

「ｙをｘの式で表しなさい」と書かれているけど、簡単に言い換えると「ｙ＝○ｘ」になるか教えてね。という意味になるんだよ。

「ｙ＝○ｘ」の「○」に入る数がわかればOK。

STEP２
じゃあどうやって○の数を求めるかを考えよう。

グラフを見て、「キリのよい点」の座標を読み取ろう。

今回は（２、４）として考えてみたよ。

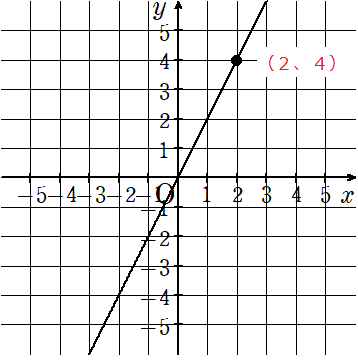
STEP３
（２、４）って、ｘ座標が「２」で、ｙ座標が「４」ということだよね。じゃあ、「２」と「４」をどうしたらいいかわかる？

ここがこの問題の一番のポイント！！

答えは「ｙ＝○ｘ」に代入する！！

「ｙ＝○ｘ」にｘ＝２とｙ＝４を代入してみよう。
○ではなくて「ａ」を使って考えるよ。

　ｙ＝ａｘ　　　←ｘに２、ｙに４を代入する。
　４＝ａ×２　　
　４＝２ａ　　　←左辺と右辺を入れ替える
２ａ＝４　　　　←両辺を２で割る
　ａ＝２

○に入る数が「２」とわかったらから、答えは「ｙ＝２ｘ」になるよ。

たろう

比例の式「ｙ＝ａｘ」と「代入のやりかた」がわかっていればできるね。

（例題）

次のグラフはｙはｘに比例している。ｙをｘの式で表しなさい。

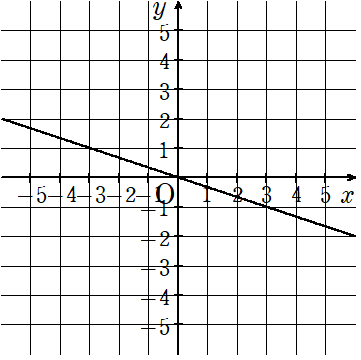
STEP１

「ｙ＝○ｘ」の「○」に入る数がわかればOK。

STEP２

グラフを見て、「キリのよい点」の座標を読み取ろう。

今回は（－３、１）として考えてみたよ。

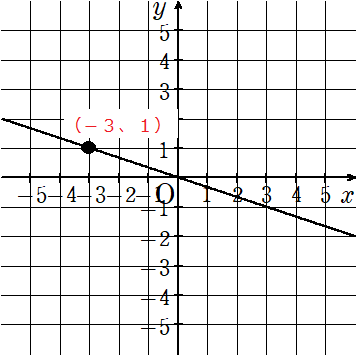
STEP３
（－３、１）って、ｘ座標が「－３」で、ｙ座標が「１」ということだよね。

「ｙ＝○ｘ」にｘ＝－３とｙ＝１を代入してみよう。
○ではなくて「ａ」を使って考えるよ。

　　ｙ＝ａｘ　　　　　　←ｘに－３、ｙに１を代入する。
　　１＝ａ×（－３）　　
　　１＝－３ａ　　　　　←左辺と右辺を入れ替える
－３ａ＝１　　　　　　　←両辺３で割る
　－ａ＝\(\frac{１}{３}\)　←「－」が残っているから、両辺「－１」をかける
　　ａ＝－\(\frac{１}{３}\)

○に入る数が「－\(\frac{１}{３}\)」ってわかったらから、答えは「ｙ＝－\(\frac{１}{３}\)ｘ」になるよ。

こうやって、比例のグラフから比例の式を求めるよ。
グラフから比例の式を求める問題は入試問題にもよく出るし、２年生、３年生でもかなり重要な知識だからしっかり覚えておこう。

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。