「多項式と単項式の乗法・除法」のやり方をわかりやすく解説
中学3年生の数学で学習する「多項式と単項式の計算」について、「多項式と単項式の乗法」「多項式と単項式の除法」それぞれどんな問題が出るのか、問題パターンごとの解き方をくわしく解説するよ。
単項式と多項式の違いをおさらいしよう
単項式と多項式の違いは覚えているかな?2年生で学習したよね。忘れてしまっている人はおさらいをしよう。
単項式とは
単項式っていうのは、「数や文字についての乗法(かけ算)だけで作られた式」のことだよ。
例えば、2xだったら、2×xって表せるよね。だから単項式といえるよ。
※数字と文字の間に【+】や【-】が無い式と覚えておこう!
多項式とは
逆に多項式っていうのは、単項式の和(足し算)や差(引き算)の形で表された式のことだよ。
例えば、2x+yだったら、2xとyの間に足し算が入っているよね。だから多項式なんだ。
項の数で多項式と単項式を見分ける
もっと簡単に見分けるには、「項の数」に注目してみよう。
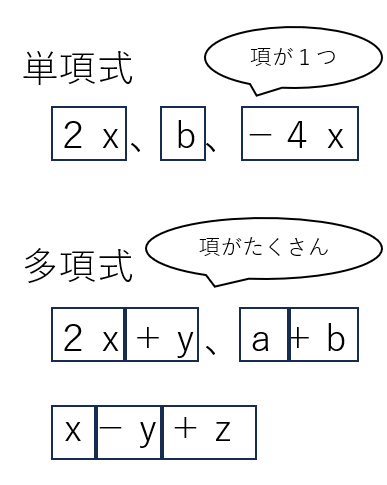
多項式と単項式の違い
多項式:項が2つ以上 (例)2x+y、a+b、x-y+z
単項式:項が1つ (例)2x、b、-4x
多項式と単項式の乗法
多項式と単項式の乗法の計算を考えよう。2年生の内容がわかっていたら、簡単にできちゃうと思うよ。
2年生のおさらい
2年生ではこんな計算をやったよね。
4(2a-3b) ←分配法則を使う
=4×2a+4×(-3b)
=8a-12b
分配法則を使えてしまえば楽勝な問題だね。3年生になると2年生より少しだけレベルアップするよ。
2年生と3年生の違い
2年生:4(2a-3b) → 数×(多項式)
3年生:4a(2a-3b) →単項式×(多項式)
2年生では「数×(多項式)」だったのが、3年生になると「単項式×(多項式)」になるんだよ。
多項式と単項式の乗法の例題
多項式と単項式の乗法は2年生でやった「4(2a-3b)」の計算の仕方と全く同じだよ。
じゃあ実際に次の例題をやってみよう。
4a(2a-3b) ←分配法則を使う
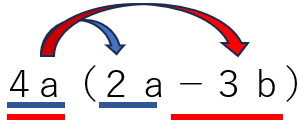
=4a×2a+4a×(-3b)
=8a2-12ab
気を付けること
・4a×2aの計算は、数字同士、文字同士をかけること
・a×a=a2になること
・-3bには( )をつけること
多項式と単項式の乗法の練習
多項式と単項式の乗法の練習をして、計算に慣れていこう。
(1)
3a(-2a-4b)
=3a×(-2a)+3a×(-4b)
=-6a2-12ab
よくある間違い
3a(-2a-4b)
=3a×(-2a)3a×(-4b)
2つ目の3aの前に符号(+か-)がないよ。「3a(-2a-4b)」の3aの前には「+」が省略されているから次のようになるよ。
+3a×(-2a)+3a×(-4b)
(2)
(3a-2b)×4b
=3a×4b-2b×4b
=12ab-8b2
後ろからかける問題
「(3a-2b)×4b」は後ろから「4b」をかけていくよ。下の2つは同じことだから、もし①のやり方が難しかったら、②のやり方でやるのもありだね。
① (3a-2b)×4b
② 4b(3a-2b)
(3)
-2a(3a-4b-c)
=-2a×3a-2a×(-4b)-2a×(-c)
=-6a2+8ab+2ac
多項式の項の数が3つの問題
「-2a(3a-4b-c)」の「-2a」を順番に、「3a」「-4b」「-c」にかけるだけだよ。
(4)
最後に次の問題に挑戦してみよう
2a(a+b)-3a(a-b)
式を見た瞬間、「難しそう」って思うかもしれないけど、2つに分けて考えたら簡単だよ。
2a(a+b)-3a(a-b)を
2a(a+b) と -3a(a-b) にわけて計算しよう。
2a(a+b) -3a(a-b)
=2a×a+2a×b -3a×a-3a×(-b)
=2a2+2ab -3a2+3ab
ここまでいったら、同類項(文字の部分が同じ項)を計算しよう。
2a2+2ab -3a2+3ab
=2a2-3a2+2ab+3ab
=-a2+5ab
多項式と単項式の除法
多項式と単項式の除法(割り算)の計算を考えよう。2年生の内容とさっきの内容がわかっていたら、簡単にできちゃうと思うよ。
2年生のおさらい
2年生ではこんな計算をやったよね。
(12a-8ab)÷4 ←割り算をかけ算にすると「逆数」になるよ。
=(12a-8ab)×\(\frac{1}{4}\)
=12a×\(\frac{1}{4}\)-8ab×\(\frac{1}{4}\)
=3a-2ab
逆数にして、分配法則を使えてしまえば楽勝な問題だね。3年生になると2年生より少しだけレベルアップするよ。
2年生と3年生の違い
2年生:(12a-8ab)÷4 → (多項式)÷数
3年生:(12a-8ab)÷4a → (多項式)÷単項式
2年生では「(多項式)÷数」だったのが、3年生になると「(多項式)÷単項式」になるんだよ。
逆数のおさらい
わり算をかけ算にすると、逆数になるよ。逆数っていうのは「分母」と「分子」を入れ替えた数のことだよ。
例えば、
4÷\(\frac{3}{2}\)だったら
4×\(\frac{2}{3}\)になるよ。わり算をかけ算にすると、分母と分子が入れ替わっていることを確認しよう。
多項式と単項式の除法の例題
多項式と単項式の除法は2年生でやった「(12a-8ab)÷4」の計算の仕方と全く同じだよ。
じゃあ実際に次の例題をやってみよう。
(12a-8ab)÷4a ←わり算をかけ算にすると「逆数」になる。
=(12a-8ab)×\(\frac{1}{4a}\) ←分配法則を使う
=12a×\(\frac{1}{4a}\)-8ab×\(\frac{1}{4a}\)
=3-2b
気を付けること
・「4a」は分数であらわすと「\(\frac{4a}{1}\)」になるから、逆数にしたら「\(\frac{1}{4a}\)」だよ。
・「12a×\(\frac{1}{4a}\)」って次のように計算できるよ。aが約分して消えることに注意しよう。
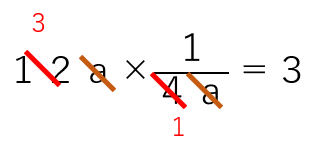
多項式と単項式の除法の練習
多項式と単項式の除法の練習をして、計算に慣れていこう。
(1)
(4a2-2a)÷2a ←逆数にする
=(4a2-2a)×\(\frac{1}{2a}\) ←分配法則
=4a2×\(\frac{1}{2a}\)-2a×\(\frac{1}{2a}\)
=2a-1
気を付けること
・「2a」を逆数にすると、「2」だけではなく、「a」も分母になることを忘れないようにしよう。(\(\frac{1}{2}\)aは間違い)
・「4a2×\(\frac{1}{2a}\)」の約分の計算に気を付けよう。
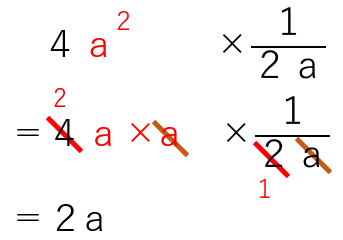
(2)
次の問題は少し難しいよ。
(9a2b-6ab2)÷\(\frac{3}{2}\)ab
まず、わり算をかけ算にして逆数にするんだったよね。ただ、\(\frac{3}{2}\)abを逆数にするのが難しいね。
\(\frac{3}{2}\)abを逆数にする
「\(\frac{3}{2}\)ab」の横についている「ab」っていうのは、分母か分子のどちらかに移動できるんだけど、どっちかわかるかな。
分数の横についている文字は「分子(上)」に移動することができるんだ。だから、「\(\frac{3}{2}\)ab」は「\(\frac{3ab}{2}\)」と表せるよ。
これを逆数にすると
\(\frac{3ab}{2}\)→\(\frac{2}{3ab}\)
じゃあ、わり算をかけ算にして逆数にしてみるよ。
(9a2b-6ab2)÷\(\frac{3}{2}\)ab
=(9a2b-6ab2)×\(\frac{2}{3ab}\)
ここまでできちゃえば、あとは分配法則が使えたらできるよ。
9a2b×\(\frac{2}{3ab}\)-6ab2×\(\frac{2}{3ab}\)
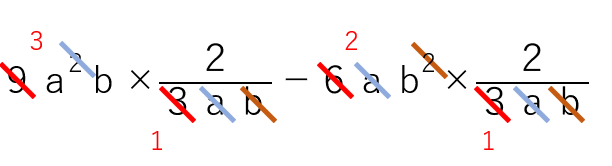
=6a-4b
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。



わかりやすい