いろいろな作図「円の接線・円の中心・30°の角度」の書き方を解説
中学１年生の数学で学習した、「基本の作図」で書けるようになった図の性質を使って、いろいろな作図をする方法を紹介するよ。
「円の接線」、「円の中心」そして「ある大きさの角」を書くための考え方や手順を、くわしく解説していくよ。
いろいろな作図 「円の接線・円の中心・30°の角度」の 書き方を解説のPDF（13枚）がダウンロードできます。
PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。
目次
円の接線を作図してみよう
円の接線とは
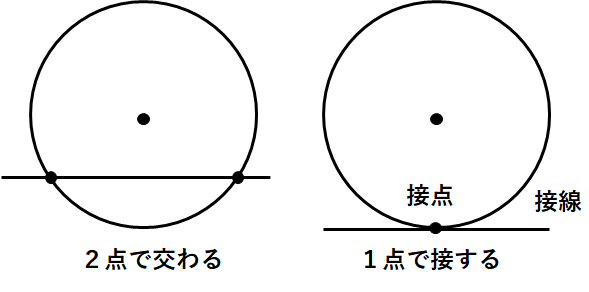
円の接線とは、円と直線がただ1点だけで接するときの直線のことだよ。
「接する」というのは、触れ合っているとか、つながるという意味があるよ。
下の図で言うと、右側のような状態の直線のことを接線っていうよ。
左側は「２点で接している」から接線ではないということだね。
円の接線の性質
円の接線の大切な性質は、「接点を通る半径に垂直」になるということ。
どういうことかというと下の図を見てみよう。
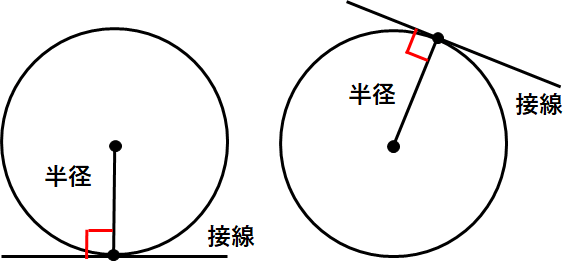
「円の接線が接点を通る半径に垂直になる」という性質は接線の１番大切な性質なので、高校生でも使うから覚えておこう。
円の接線の書き方
それでは円の接線をコンパスと定規を使って書いていこう。
さっき「円の接線は、接点を通る半径に垂直になる」という性質を紹介したけれど、円の接線の作図では、この性質を使って作図するよ。
例題：下図のような円Оで、接点Tを通る円の接線を作図しなさい。
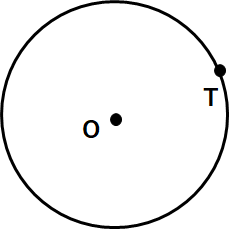
まずはなんとなく作図のイメージをしてみよう。
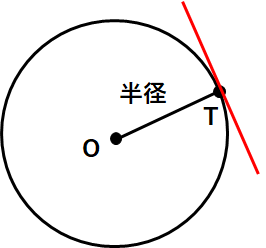
円の接線の性質は、「接点を通る半径に垂直」になるというものだったよね。
では、まず「OT」を結んでみよう。これが半径になるね。
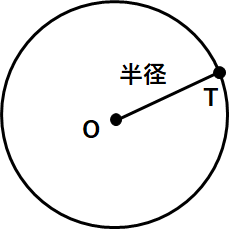
線分OT（半径）に垂直になる直線を引くことができれば、円Oの接線の出来上がりだよね。
イメージはこんな感じかな。
実際に作図をしてみよう。
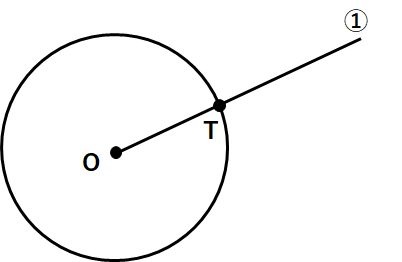
①半直線OTを引こう。
ここからは「垂線の作図」と同じだよ。
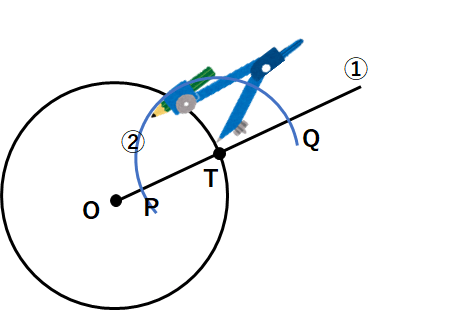
②コンパスの針を点Tに刺して、適当な半径で円の一部を書こう。
半直線OTと交わったところを点P、点Qとしよう。
③コンパスの針を点Pにさして、適当な半径で円の一部を書こう。
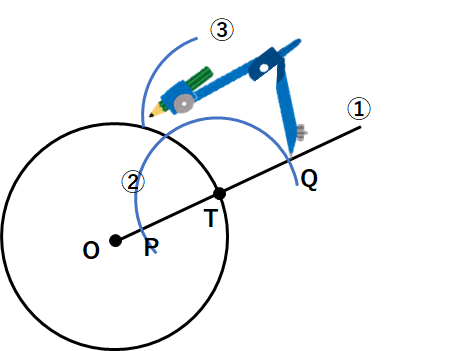
④コンパスの針を点Pにさして、③と同じ半径で円の一部を書こう。③と交わったところを点Rにしよう。
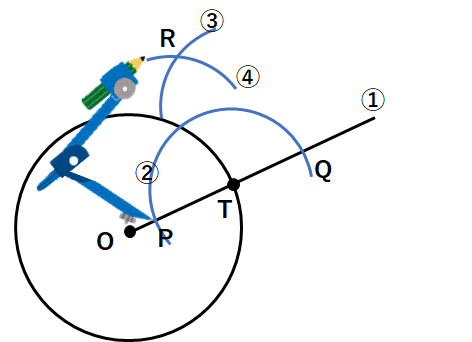
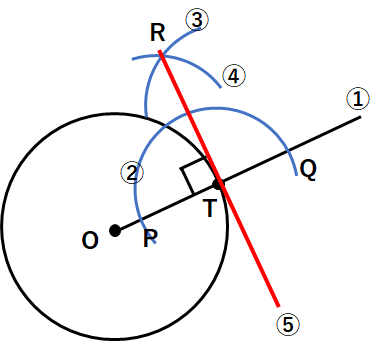
⑤直線RTを引いたら、円Oの接線が完成するよ。
円の中心の求め方
それでは、こんどは「円の中心」を作図で求める方法を紹介するよ。
下図のような円があったとしよう。円の中心はどうやって見つければよいだろう？
実は垂直二等分線を使うと、円の中心が求められるんだよ。
垂直二等分線の性質
垂直二等分線にはすごく大切な性質があるんだったよね。
下図のように、垂直二等分線の上にある点と、点A、点Bとの距離は等しくなるね。
もう少し簡単に言うと、垂直二等分線（赤線）の上であったら、必ずAP=BPになっているよ。
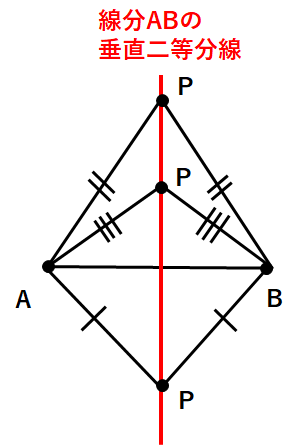
この性質を使って、円の中心を求めよう。
円の中心とはどんな点？
円の中心とは、どんな点なのか考えてみよう。
円の中心は、円周の上のどの点からの距離が等しいよね。
円の中心が点Oだったとすると、点Oは、点Aからも点Bからも点Cからも等しい距離にあるってことだよね。
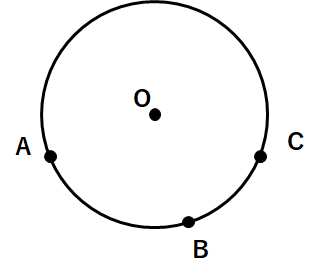
点Oが点Aからも点Bからも点Cからも等しい距離にあるということは、
点Oは
- ①点A、点Bから等しい距離にある。
→中心Oは、線分ABの垂直二等分線の上にある。 - ②点B、点Cから等しい距離にある。
→中心Oは、線分BCの垂直二等分線の上にある。
ということだよね。
円の中心を作図で求めてみよう。
では実際に円の中心を作図で求めてみよう。
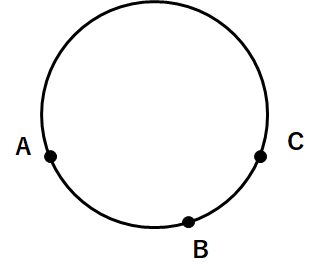
下図のような円の中心を作図によって求めなさい。
垂直二等分線を２つ書いて、円の中心を求めよう。
①３点A、B、Cをとろう。
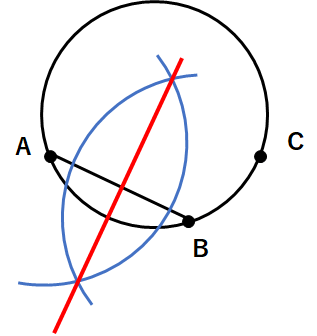
②線分ABの垂直二等分線を作図しよう。
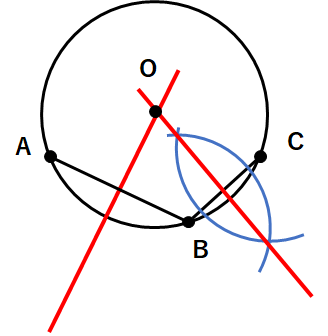
③線分BCの垂直二等分線を作図して、②の垂直二等分線と交わったところが円の中心Oだよ。
３０°の角度を作ろう
コンパスと定規を使って３０°の角度を作図してみよう。
作図するには２つのことをしなくちゃいけないんだ。
１つ目が正三角形を書くこと。
２つ目が角の二等分線を書くこと。
正三角形は１つの角度が６０°だよね。６０°を二等分したら３０°になるから、正三角形を書くんだよ。
では、順番にやっていこう。
１：正三角形を書こう
正三角形は３つの辺の長さが等しい三角形だよね。
なので、３つの等しい長さの直線を引くことで作図ができるよ。
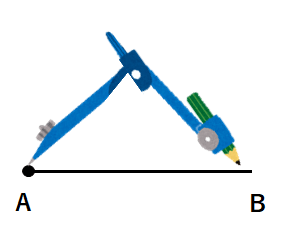
①適当な長さを定規で引くよ。
②コンパスで、その線の長さ分広げよう。
なぜなら、等しい長さの直線を引くためだね。
③点Aにコンパスの針をさして、円の一部を書こう。
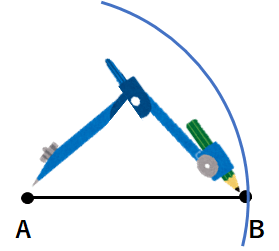
④点Bにコンパスの針をさして、円の一部を書こう。③と交わったところが点Cになるよ。
なぜなら、点Ｃは、点Ａから線分ＡＢと等しい距離、
そして点Ｂからも線ＡＢと等しい距離のところにある点だからね。
これで、「３つの長さが等しい辺」を書くことができるよね。
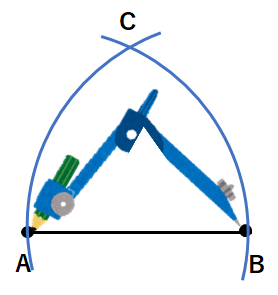
⑤A、B、Cを結んだら、正三角形の完成だよ。正三角形の１つの角度は６０°だったよね。
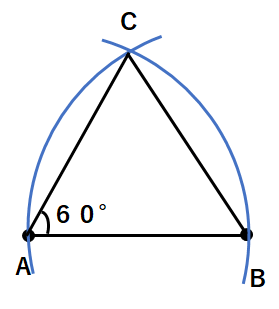
２：角の二等分線を書こう
∠Aが６０°だから、∠Aの二等分線を引いたら、３０°が作図できるよね。
角の二等分線の書き方は、「基本の作図の書き方」の解説ページを確認しよう。
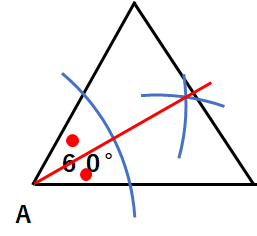
赤線が角の二等分線だから、赤丸が３０°ということになるよ。
なぜなら、６０°の∠Aを半分にしているんだから、
６０÷２＝３０
となるからだね。
基本の作図をつかえば、いろいろな図が書ける
この方法をうまく利用すれば、３０°だけではなく、１５°や７５°も書けそうだね。
ポイントは、正三角形を作図できれば、６０°の角を作ることができるんだから、あとはその「６０」を使ってどうやって「１５」や「７５」を作り出すか考えればいいんだよ。
「６０」を一度二等分すれば「３０」になったよね。
なら、あともう一度二等分すれば「１５」になるよね。
「７５」は、「６０」に「１５」を足すことで作ることができるよね。
「６０」も「１５」も作ることができるんだから、
まず正三角形を書いて「６０」を作って、その「６０」にぴったりくっつくように別の正三角形を書いて「６０」を作って、
その「６０」を二等分して「３０」にして、
またその「３０」を二等分して「１５」にしてあげれば、
もとの１つ目の正三角形の「６０」と、２つ目の正三角形の「１５」をたして「７５」のできあがりというわけだね。
このように、「基本の作図」をマスターしていれば、正三角形とか、二等分線とか、垂直の線とか、その書けるようになったものをうまく利用して、いろいろな作図をすることができるんだよ。
基本の作図のワザをつかって、どうすればお題の図を書くことができるだろう、と自分で工夫して考えるのはなかなか楽しいね。
コツとしては、「その図」は、どういう性質をもっているのか？をまず理解して、覚えること。
たとえば、「正三角形」を書けば「正三角形は、３つの角がすべて６０°になる」という性質によって、６０度の角を作り出すことができる。
「垂直二等分線」を書けば、「１つの直線に垂直に交わる直線」という性質によって、「垂直な２つの直線」や「９０°の角」を作り出すことが出来る。
また、「垂直二等分線を書くためにとった２つの点から、垂直二等分線上のどの点までの距離はそれぞれ等しい」という性質によって、「等しい距離にある点」を探し出すことができたり。
正三角形や、垂直二等分線、円を書く「方法」が「ワザ」、
それぞれの図の性質によって、できあがる「直線」や「６０°の角」や「等しい距離の点」などが、「道具」ということ。
その「ワザ」と「道具」を使って、どうすれば新しい図を生み出せるのかな、と考えるということだね。
運営者情報
ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。
