文字式の利用（数の表し方）等式・不等式とは？わかりやすく解説
中学１年の数学で学習する「文字式の利用」について、数の表し方と、どうしてその表し方ができるのかをわかりやすく解説するよ。
等式・不等式とは何か、どうやって数量の間の関係を表すのかをくわしく説明するよ。
目次
数の表し方
「文字式の利用」って、言葉だけだとなんのことかピンとこないよね。
中学数学に入ると、ａとかｘとかいろんな文字を使う「文字式」を学習したよね。
その「文字式」を利用して、いろいろ出来るようになろう、というのがこの単元「文字式の利用」だよ。
今回は文字を使って、「３の倍数」や「奇数」や「偶数」といった数字を表す方法を学習するよ。
たろう文字を使って数字を表すってどういうこと？
先に答えを言ってしまうと、次の通りになるよ。
整数をｎとすると、数字は次のように表すことができる
- ３の倍数は「３ｎ」と表せる
- 偶数は「２ｎ」と表せる
- 奇数は「２ｎ＋１」や「２ｎ－１」と表せる
この３つをそのまま覚えてしまってもいいけれど、なんでこうなるかを考えることで理解が深まるよ。
３の倍数は「３ｎ」と表せる
まず３の倍数がどんな数かを考えよう。３の倍数の例をあげると、
３、６、９、１２、・・・
だよね。
３、６、９、１２って、こんな感じで、別の書き方でも表すことができるよね？
３＝３×１
６＝３×２
９＝３×３
１２＝３×４
つまり、
３の倍数＝３×（整数）って書き方でも表すことができるよね。
３の倍数のことは、「３×整数」と表すことができることがわかったね。
数学では、整数のことを表すのに、一般的に「ｎ」という文字を使うんだ。
「ｎ」は、数字（number）の頭文字の「ｎ」だよ。
そうすると、
３の倍数＝３×（整数）は
３×ｎになって、文字式のルールで×（かける）は省略するので、
＝３ｎ
と、表せるというわけなんだ。
偶数は「２ｎ」と表すことができる
まず、偶数って「２で割り切れる数」のことなんだから、つまり「２の倍数」だよね。
だから、３の倍数のときと、同じような感じで、２の倍数（偶数）を考えよう。
２の倍数（偶数）ってどんな数か例をあげると、
２、４、６、８、１０、・・・だよね？
２、４、６、８、１０ってこんな感じで別の書き方でも表すことができるよね？
２＝２×１
４＝２×２
６＝２×３
８＝２×４
２の倍数＝２×（整数）って表現できるよね。
３の倍数のときと同じように、「整数ｎ」を使うと
２の倍数＝２×（整数）
＝２×ｎ
＝２ｎ
と表せるよ。
奇数は「２ｎ＋１」や「２ｎ－１」と表すことができる
奇数ってどんな数かを例をあげると、
１、３、５、７、・・・だよね。
偶数と奇数は、かわりばんこに並んでいるので、奇数はかならず偶数より１少ないか、偶数より１多くなっているよね。
ということは、奇数って次のように表せることがわかるかな？
- 奇数＝偶数＋１
- 奇数＝偶数－１
たろう当たり前だね。偶数に１を足したり、１引いたりしたら奇数になるよね。
そうすると、さっき説明したように、「偶数」は「２ｎ」と表すことができるんだったから、奇数のことは次のように表すことができるんだ。
- ２ｎ＋１
- ２ｎ－１
２つあるんだけれど、どちらでも好きなほうを使ってOK。
それでは、ちょっと練習問題を考えてみて、より深く理解できるようにしよう！
【問題】どんな数を表しているでしょうか？
整数をｎとしたとき、次の数はどんな数を表しているかな？
（１）５ｎ
答えは「５の倍数」だよ。なんでかというと、５ｎって５×ｎのことだからね。
確かめるために、実際に「ｎ」に整数を入れてみよう。
ｎ＝１だったら５×１＝５
ｎ＝２だったら５×２＝１０
ｎ＝３だったら５×３＝１５
５、１０、１５って５の倍数だよね。だから、５ｎは５の倍数を表すよ。
（２）９ｎ
答えは「９の倍数」だよ。なんでかというと、９ｎって９×ｎのことだから。実際に「ｎ」に整数を入れてみよう。
ｎ＝１だったら９×１＝９
ｎ＝２だったら９×２＝１８
ｎ＝３だったら９×３＝２７
９、１８、２７って９の倍数だよね。だから、９ｎは９の倍数を表すよ。
文字式を利用して整数の性質をあらわそう
さっき説明した「文字式を利用して数を表す方法」は次の３つだったよね。
整数をｎとすると次のように表すことができる
- ３の倍数は「３ｎ」
- 偶数は「２ｎ」
- 奇数は「２ｎ＋１」や「２ｎ－１」
これらの方法を利用して、今度は「整数の性質」を表してみよう。
「整数の性質をあらわす」というのはどういうことかというと、「○○な数は、どんな数になるか」を説明するということだよ。
考えてみてもらいたい問題は下の問題だよ。
問１
２つの続いた整数の和はどんな数になるか？
２つの続いた整数っていうと、たとえば次のような数だよね。
１と２
２と３
５と６
１０と１１
その和はどうなるかというと、実際に計算してみるとこうなるよ。
１＋２＝３
２＋３＝５
５＋６＝１１
１０＋１１＝２１
くまごろう３、５、１１、２１を見てなにか気づいたかな？
たろう全部奇数になっているね！
そう、２つの続いた整数の和は奇数になる性質があるんだ！
これが、「〇〇な数はどんな数か」ということだね。「２つの続いた整数の和は奇数」ということ。これが「整数の性質」。
今回学習するのは、この「整数の性質」を、文字式を使って表そう、ということだったね。
整数の性質を文字式を使ってあらわすには、「なんでそうなるか？」を文字を使って考えてみればいいんだよ。
問２
２つの続いた整数の和は奇数になることを文字で考えてみよう。
２つの続いた整数の和が奇数になることを説明してみよう。次の２つのステップに分けて説明するね。
①２つの続いた整数を文字「ｎ」であらわそう。
例えば、３と４っていう「２つの続いた整数」で考えてみよう。
３と４ってこんな風に言い換えられるよね。
「３と、３＋１」
なぜなら、２つ整数は続いているんだから、小さい方の整数に１を足せば、もうひとつの整数になるよね。
なので、小さい方の３に１を足したら大きい方の４になるよね。
だから、「３と、３＋１」と表すことができるんだね。
じゃあ、ここに整数を表す「ｎ」を使ってみよう。
２つあるうち、小さい方をｎってすると、大きい方はｎ＋１になるよね。
②２つの和を考えよう。
「２つの続いた整数の和」がどんな数かをもとめるんだから、この２つの整数の和を考えてみるよ。
小さい方の数がｎ、大きい方の数がｎ＋１だから、
その和は
ｎ＋（ｎ＋１）
＝ｎ＋ｎ＋１
＝２ｎ＋１
になるね。
ここで、２ｎ＋１ってどんな数だったかというと、そう、「奇数」だったよね。
だから、２つの続いた整数の和は奇数になるんだよ。
「○○な整数は✖✖な数になる」という整数の性質を、どうしてそうなるのか、文字式を使って説明することができたね。
数量の間の関係の表し方
「数量の間の関係」なんて言葉を急に言われても、頭に「？」が浮かぶ人が多いと思うから、中学校レベルの問題の前に、小学校の問題を紹介するよ。
りんご３個がありました。４個買いました。合わせると７個になります。この数量の関係を表しなさい。
答えは、
３＋４＝７
これが小学生レベルの問題だよ。
「数量の関係」というのは、それぞれの数量の間に、「関係がある」ということ。
「３＋４」と、「７」は、「おんなじ」という関係だよね。
「３＋４」と、「６」だったらどう？
ことばで関係を説明するなら、「３＋４」は、「６」よりも大きくなる、とかかな。
これから学習するのは、こういった数量の関係を、文字やいろいろな記号で説明するようにしよう、ということなんだ。
小学生と中学生の違い
- 文字が登場する
- 「＝」だけでなく「＜、≦、＞、≧」が登場する。
ちなみにこの「＝（イコール）」のことは「等号」と呼ぶよ。
そして、「＝（イコール)」で結ばれた式のことを「等式」っていうよ。
「等号」の「等」は、「等しい」という意味だよね。
つまり、「おんなじ」ということを表す記号と、式ということだね。
中学生になると「等号」を使った「等式」だけではなく、
不等号「＜」「＞」を使った「不等式」というのを勉強するようになるんだ。
等式と不等式を順番に紹介していくね。
等式とは
等式っていうのは、数や文字、式などが等号「＝」で結ばれた式のことだよ。
例えば、こういうのを等式っていうよ。
・５０ｘ＋３０＝９３０
・４ｘ＝３ｙ
たろう「＝」で結ばれた式を等式というんだね。
じゃあ、等式を作る練習をしていこう。
（１）１２０円のリンゴｘ個と１８０円のバナナ１個を買ったら１０００円になった。
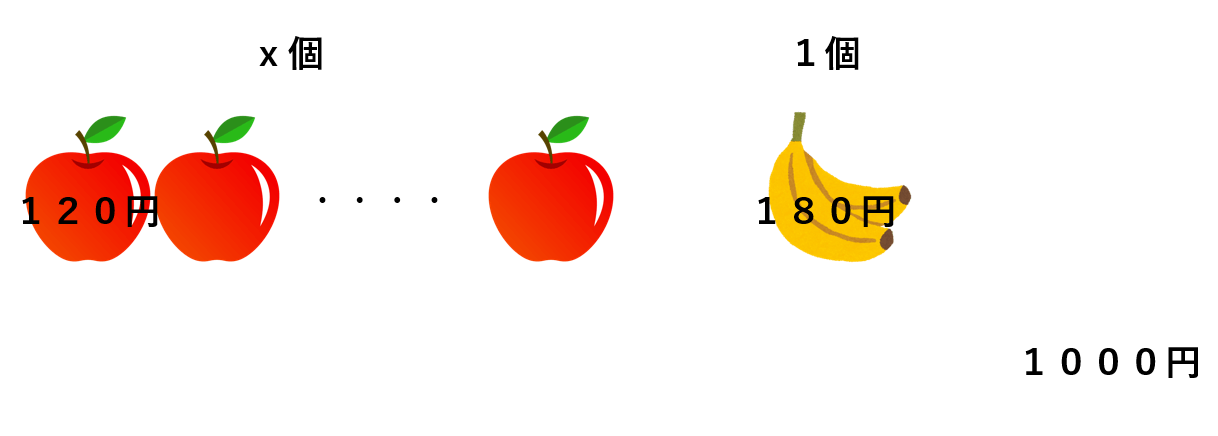
①１２０円のリンゴｘ個だから、リンゴだけで１２０ｘ円
②リンゴｘ個の値段１２０ｘ円とバナナ１８０円の値段を足したら１２０ｘ＋１８０円になる
③１２０ｘ＋１８０が１０００円になるから
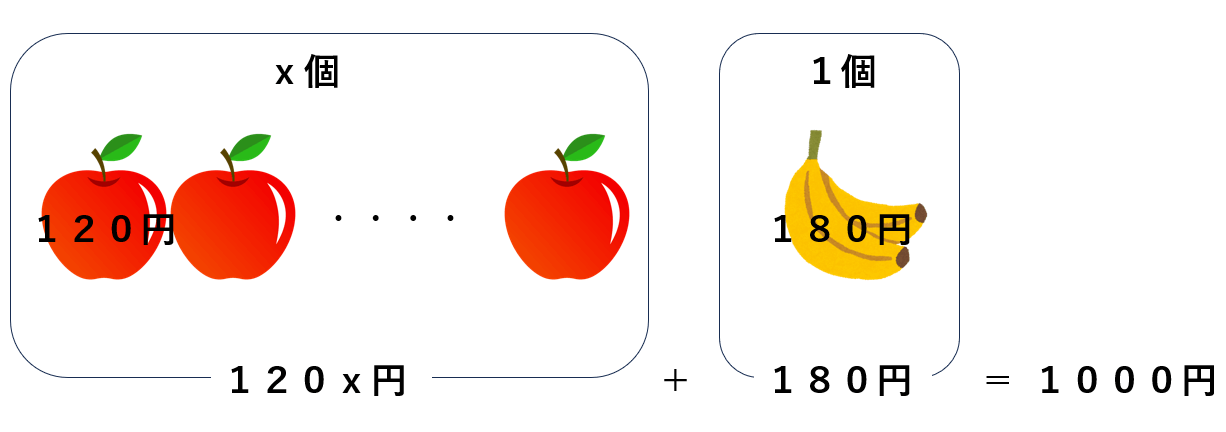
１２０ｘ＋１８０＝１０００
という等式が完成するよ。
「右辺」と「左辺」とは
ここで、ひとつ新しく登場することばがあるよ。それは「右辺」と「左辺」。
等式の、「＝（イコール）」の右側のことを、「右辺」、左側のことを「左辺」と呼ぶんだ。
たとえば、この等式の場合、「＝（イコール）」の右側にある、１０００が「右辺」だね。
「＝（イコール）」の左側にある、１２０ｘ＋１８０が「左辺」だよ。
（２）１冊ｘ円のノート３冊と、６０円の鉛筆１本を買ったとき、代金の合計は１２０円だった。
①１冊ｘ円のノート３冊だから、３ｘ円
②ノート３冊の値段３ｘと鉛筆６０円の値段を足したら３ｘ＋６０になる
③３ｘ＋６０が１２０になるから
３ｘ＋６０＝１２０
という等式が完成するよ。
右辺は「１２０」
左辺は「３ｘ＋６０」だね。
（３）１２０円のカレーパンｘ個と２００円の牛乳を買ったときの代金は１６０円のコロッケパンｙ個を買ったときの代金と等しい。
①１２０円のカレーパンｘ個だから、１２０ｘ円
②カレーパンｘ個の値段１２０ｘ円と２００円の牛乳の代金を足したら１２０ｘ＋２００になる
③１６０円のコロッケパンｙ個だから、１６０ｙ円
④１２０ｘ＋２００が１６０ｙになるから
１２０ｘ＋２００＝１６０ｙ
という等式が完成するよ。
右辺は「１６０ｙ」
左辺は「１２０ｘ＋２００」だね。
不等式とは
教科書数の大小関係を示す「不等号」（＞・＜・≧・≦）を使って表した式のことを不等式という
不等号の確認をしよう！
不等号は大きい方に開くんだったよね。
たとえば、「５は３よりも大きい」ことを表すには、「３＜５」というように使うんだったね。
では、「＜」と「≦」はなにが違うんだろう？
ポイントは「その数を含むかどうか」だよ。
（例）太郎の身長を「ｘ」だとして、ｘ＜１００ と ｘ≦１００の違いを考えよう（単位ｃｍ）
①ｘ＜１００だと「ｘは１００より小さい」「１００未満」
１００は入らないということだね。
「太郎の身長は１００ｃｍより小さい」から、１００ｃｍということはなくなるよ。
②ｘ≦１００だと「ｘは１００以下」
この場合は、１００も入るんだ。
太郎の身長は１００以下だから、１００ｃｍということもありえるね。
不等号の確認が終わったところで、不等号を使った「不等式」で表す練習をしていこう。
（１）１本ａ円の鉛筆３本と１個ｂ円の消しゴム２個の代金の合計は３００円より高かった。
①１本ａ円の鉛筆３本だから３ａ円
②１個ｂ円の消しゴム２個だから２ｂ円
③代金の合計は３ａ＋２ｂ円になる。
④代金の合計が３００円より高いので
３ａ＋２ｂが３００より大きい。
つまり
３ａ＋２ｂ＞３００
となるよ。
（２）長さｘｍのテープを５等分したら、１本分の長さは３ｍ以下になった。
①長さｘｍのテープを５等分すると１本分はｘ÷５＝\(\frac{ａ}{５}\)ｍになる
②１本分の長さが３ｍ以下なので
\(\frac{ａ}{５}\)は３以下
つまり
\(\frac{ａ}{５}\)≦３
となるよ。
まとめ
「等式」や「不等式」とは何かわかったかな。
等式で表すことは、このあと学習する方程式でも使う知識だよ。だから、今のうちに完璧にしておこう。
今回のポイントを下にまとめたよ。
今回のポイントまとめ
- 整数をｎとすると、３の倍数は３ｎ、偶数は２ｎ、奇数は２ｎ＋１や２ｎ－１と表す
- 等号で結ばれた式を等式と呼ぶ
- 等式の「＝」の右側を「右辺」と呼ぶ。「＝」の左側を「左辺」と呼ぶ。
- 不等号を使って表された式を不等式と呼ぶ。
- 「１００＜」は１００未満なので、１００は入らない。「≦１００」は、「１００以下」なので、１００が入る。
運営者情報
ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。
