比例式の問題とxの求め方を確認しよう!(比例式の利用と性質)
中学校1年生の数学で学習する「比例式」とはなにか、比例式の性質や「x」の求め方をくわしく解説するよ。
どんな問題が出るのか、文章問題の解き方のコツなど、比例式のテストで必要になるポイントを確認しよう。
比例式とは
比例式とは、「2つの比」が等しいことを表した式のことだよ。
比例式の形といわれたら、次のように覚えておこう。
a:b=c:d
実際の問題ではa、b、c、dにそれぞれ数字が入るよ。
例えば、9:6=3:2みたいな感じだね。
「9:6」という比と、「3:2」という比は等しいよね。
このように、「2つの等しい比」が「=(イコール)」で結ばれている式のことなんだね。
「比例式」は、このあと勉強する「比例」とは違うものだからごっちゃにならないように注意しようね。
比例式の性質
比例式の性質とは、「比例式はどんな特徴をもっているのか」ということだよね。
比例式の性質については、これだけ知っておけばOK。
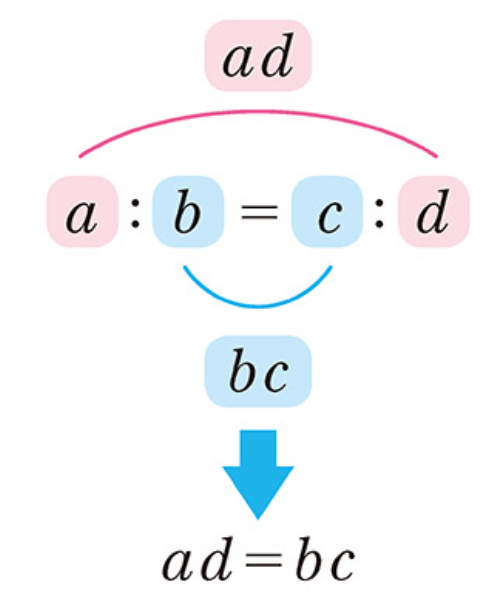
「外側をかけたもの」=「内側をかけたもの」
例えば、5:3=10:6という比例式を考えてみよう。
5:3=10:6の外側っていうのは「5」と「6」。
外側の数字「5」と「6」をかけると、
5×6=30になるね。
5:3=10:6の内側っていうのは「3」と「10」。
内側の数字「3」と「10」をかけると、
3×10=30になるね。
どうかな?
どちらも答えが「30」になって、「外側をかけたもの」=「内側をかけたもの」になることがわかったかな?
「外側をかけたもの」を「外項の積」。「内側をかけたもの」を「内項の積」というよ。
教科書では比例式の関係について、文字を使って次のように書いてあるよ。
この比例式の性質をどう使うかというと、比例式の一部が「x」になっているときに、「x」がいくつかをを求めたりする問題が出るんだ。
比例式のxの求め方
中学1年生では、比例式の一部が「x」になっているときに、「x」がいくつかをを求めたりする問題が出るんだよね。
この問題を解くポイントは、比例式の性質
「外側をかけたもの」=「内側をかけたもの」
を使っていくだけでOKだよ。
例えば、次の問題を考えてみよう。
(例)比例式x:4=8:16のxの値を求めなさい。
この程度の問題であれば、小学生でもできると思うよ。
「x:4」の割合が「8:16」になるのだから、小学生なら次のように考えるんじゃない?
小学生の考え方
x:4=8:16で、4から16で「4倍」になっている。
だから「x」を「4倍」したら8になる。
よって答えはx=2。
この問題は簡単だったから、小学生のやり方でもできたけど、中学生レベルの問題になるとそうもいかないんだ。
では、同じ問題を
「外側をかけたもの」=「内側をかけたもの」
という性質を使って解いてみよう。
x:4 =8:16 ←「外側をかけたもの」を計算するために赤同士をかけて、「内側をかけたもの」を計算するために青同士をかける。
x×16=4×8 ←「外側をかけたもの」=「内側をかけたもの」にする
16x=32
どうだろう。「16x=32」という形になったけれど、この形って、「一次方程式」だよね。
教科書では、「比例式」を「一次方程式」の単元で学習する理由はこういうことだったんだね。
「比例式」の問題は、「一次方程式」として解けばいいということを覚えておこうね。
では、さっきの続きの方程式16x=32を解いてみよう。
「x=~~」の形にするために、両辺を16で割ると、答えは「x=4」になるね。
ちなみに比例式の中の「x」を求めることを、「比例式を解く」というよ。
比例式の問題例
比例式の問題を紹介するね。使う性質は、「外側をかけたもの」=「内側をかけたもの」だから、繰り返しやって覚えてしまおう。
(問1)比例式6:10=9:xを解きなさい。
6:10=9:x ←赤同士、青同士をかける。
6×x =10×9
6x =90 ←両辺を6で割る。
x =15
(問2)比例式x:4=7:8を解きなさい。
x:4 =7:8 ←赤同士、青同士をかける。
8×x =4×7
8x =28 ←両辺を8で割る。
x =\(\frac{28}{8}\)
x =\(\frac{7}{2}\)
8x=28となってしまって、割り切れないことに少し戸惑った人もいるかな?
割り切れないときは分数すれば大丈夫。
(問3)比例式5:8=(x-2):16を解きなさい。
5:8 =(x-2):16 ←赤同士、青同士をかける。
16×x =8×(x-2)
16x =8(x-2) ←分配法則を使って、かっこ( )を外そう。
16x =8x-16
この形まで計算出来たら、あとは移項をして、方程式の解を求めるだけ。
16x =8x-16 ←「8x」を移項
16x-8x=-16
8x =-16 ←両辺を8で割る。
x =-2
比例式の文章問題の解き方
比例式の文章問題を紹介するよ。日常生活でもよく使う考え方だから、かんたんだよ。
例えば、次の問題を考えてみよう。
(例1)
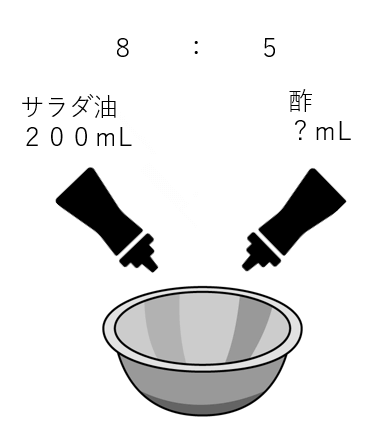
ドレッシングを作るとき、サラダ油と酢の割合は 8:5である。サラダ油がを200mL入れたとき、酢は何mL必要か求めなさい。
ステップ1:状況を図でイメージしよう。
ステップ2:求めたいものを確認する。
今回求めたいものは「酢は何mL必要か?」だよね。
一次方程式を解くときと同じように、求めたいものを「x」と置くよ。
今回は
「入れる酢の量」を「xmL」
としよう。
ステップ3:比例式をたてる。
比例式をたてるときは、問題文の中から等しい比の関係を見つけよう。
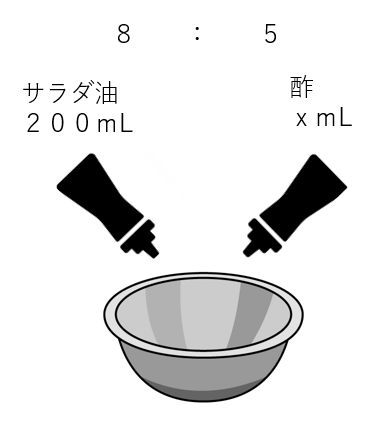
今回は「サラダ油」と「酢」の比は8:5にしなくてはいけないよね?
だから、サラダ油:酢=8:5という比例式になるよ。
200:x=8:5
順番が大事になっているから、順番を間違えないようにしよう。
今回は
実際に入れるサラダ油の量(200mL):実際に入れる酢の量(xmL)
=サラダ油の割合(8):酢の割合(5)
みたいな式になっているよ。
ステップ4:比例式を解く
比例式の性質である「外側をかけたもの」=「内側をかけたもの」を使って比例式を解いてみよう。
200:x=8:5 ←赤同士、青同士をかける。
200×5=x×8
1000=8x ←「1000=8x」も「8x=1000」も同じ
8x=1000
x=125 ←両辺を8で割る。
入れる酢の量をxmLとしたから、酢の量は125mLだということがわかるね。
(例2)
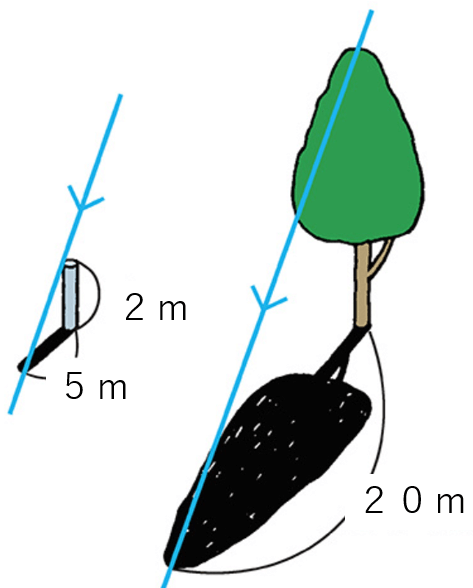
高さが2mの棒の影の長さを測ったところ、5mでした。このとき、影の長さが20mの木の高さは何mですか。
ステップ1:図でイメージする。
ステップ2:求めたいものを確認する。
赤字のところが今回求めたいものだよね。一次方程式でもそうだったけど、求めたいものを「x」と置くので、今回は
木の高さをxm
とします。
ステップ3:比例式をたてる。
比例式をたてるときは、等しい比の関係を見つけるよ。
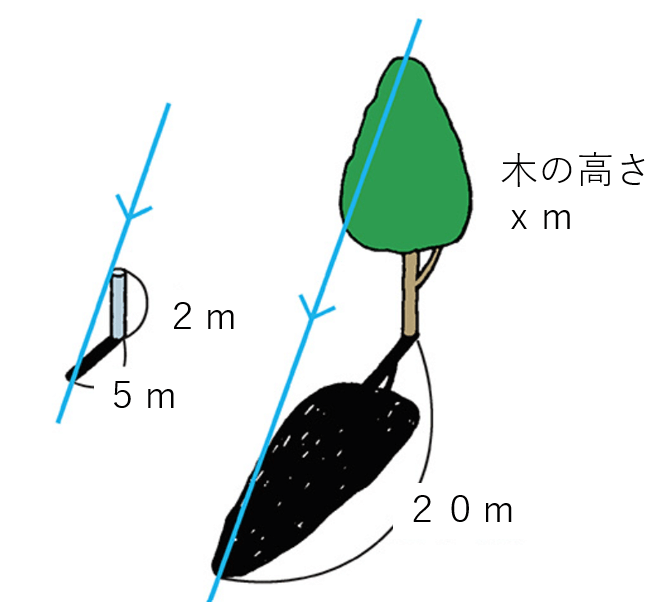
今回は「実際の高さ」と「影」の比は同じになるはずだよ。だって、棒と木は近くにあるのだから、影のでき方も同じになるはず!棒は南に影ができて、木は北に影ができるなんてありえないよね。
「実際の高さ」と「影」の比は同じになるという関係を使って比例式を作ろう。
比例式を作ると2パターン出てくると思う。
①棒の高さ:木の高さ=棒の影:木の影
②棒の高さ:棒の影=木の高さ:木の影
今回は①で比例式をたてると、次のようになるよ。
2:x=5:20
順番が大事になっているから、順番を間違えないようにしよう。
ステップ4:比例式を解く
比例式の性質である「外側をかけたもの」=「内側をかけたもの」を使って比例式を解いてみよう。
2:x=5:20 ←赤同士、青同士をかける。
2×20=x×5
40=5x ←「40=5x」も「5x=40」も同じ
5x=40
x=8
木の高さをxmとしたから、木の高さはは8mだということがわかるね。
まとめ
「比例式とは何か」
「比例式の性質とは何か」
わかったかな?比例式のポイントは「外側をかけたもの」と「内側をかけたもの」が等しくなるという性質があるよ。
比例式は日常生活でも役立つ知識なのでできるようにしておくと便利だと思うよ。
今回のポイントを下にまとめるね。
今回のポイント
・比例式とは2つの等しい比を=で結んだもので、
a:b=c:dのような形のもの
・比例式と比例とは違う
・比例式には、「外側どうしをかけたもの」=
「内側どうしをかけたもの」という性質がある。
・文章問題を解くときは、等しい比の関係を見つけることが大切
・比例式を立てるときは、それぞれの順番が大切なので注意すること。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。



