平行移動・回転移動・対象移動とは？わかりやすく解説「平面図形」
中学１年生の数学で学習する「平面図形」について、「直線AB」や三角形の表し方などの基本事項、図形の平行移動・回転移動・対象移動、垂直二等分線とは何かをわかりやすく解説するよ。
目次
図形について基本事項を確認しよう
まず、図形の学習で登場する基本的な言葉の確認をしていこう。
直線ABとは
直線ABとは、点Aと点Bを通って、下のように両側にずーっとのびている線のことをいうよ。
画面だと途中で終わっているように見えるけど、実際は、終わりなくのびているよ。
線分ABとは
直線ABとは逆に、終わりがある線のことを線分ABっていうよ。
線分ABとは、直線ABのうち、AからBまでの部分のこと。直線ABと比較するとこんな感じだよ。
直線 線分
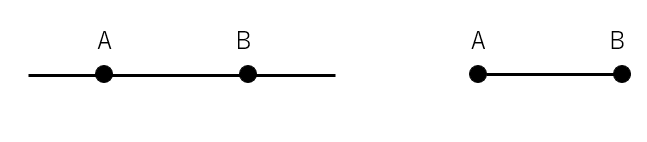
「直線AB」と「線分AB」の違い
- 直線AB：点Aと点Bを通り、どこまでものびている（線に終わりはない）
- 線分AB：直線ABのうち、AからBまでの部分。端でとまっている（線に終わりはある）
例えば、こんな問題を考えてみよう。
（例）三角形の辺の長さは直線か線分か。
答えは「線分」になるよ。だって、三角形の辺は端で止まっているよね。まさか三角形の辺がどこまでものびているなんてありえないよね。
だから三角形の辺の長さは「線分」と呼ぶよ。
半直線ABとは
直線と線分以外にも登場するのが「半直線」。
「半直線」と聞くと、「直線の半分？」とイメージしちゃうかもしれないね。
言葉で説明するより、図で表した方がわかりやすいと思うから下の図を見てみよう。
直線ABと半直線ABの違い
直線AB 半直線AB
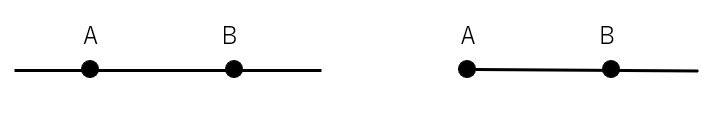
- 直線ABは両側にどこまでものびている。
- 半直線ABは点Aからスタートして、点Bの方にどこまでものびている。（点Aの方はかぎりある）
半直線というと、片側にずーっとのびている線のことをいうよ。ただ、半直線では重要なことがもう１つあるんだ。
実は、半直線ABと半直線BAでは意味が違うんだよ。
半直線ABと半直線BAの違い
半直線AB 半直線BA
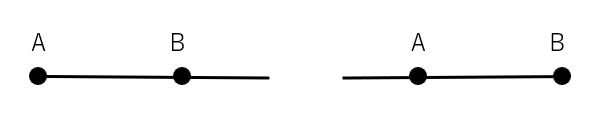
- 半直線ABは点Bの方にどこまでものびている。
- 半直線BAは点Aの方にどこまでものびている。
三角形の表し方
中学校で学習する図形の問題には「三角形」という言葉がたくさん使わているんだ。
いちいち「三角形」と書いていたら大変だから、「三角形」という言葉を「△」と省略して書くよ。
例えば、「三角形ＡＢＣ」と書きたかったら「△ＡＢＣ」と表せばＯＫ。
かなり簡単になるね。
平行移動とは
平行移動とは、図形をある方向に、ある長さだけ移動させることだよ。
平行移動の例題
（例）
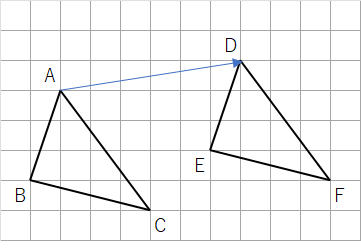
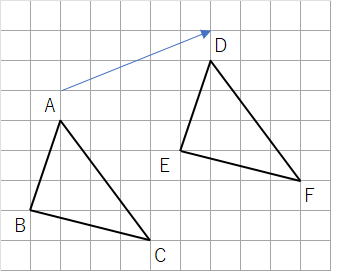
下の図の△ABCを矢印の方向に平行移動した△DEFを作図しなさい。
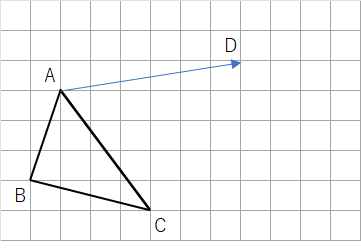
下のような移動になるよ。△ABCが矢印の方向に右に右に移動していくことがわかるね。
最後は点Aだったところが点Dまで到達したら完成だよ。
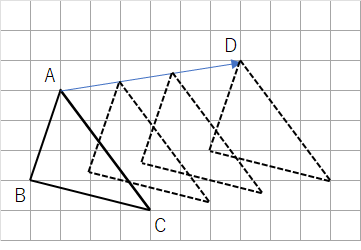
移動ができたら、「D」「E」「F」を書いておこう。問題文で「△DEFを作図しなさい」と書いてあるから、どこがD・E・Fなのかを書いておかないとダメなんだよ。
たろう平行移動ってなんか難しいな。
くまごろう辺を移動させようとするのではなくて、点を移動させようとしたらどう？
平行移動は点に注目する
平行移動だけではなく、すべての移動に言えることなんだけど・・・辺で考えると難しいから、点で考えると理解しやすいよ。
△ABCの辺をなくして、点だけにしたよ。点Aから点Dに行くまでに、右に６マス、上に１マス移動しているよね。
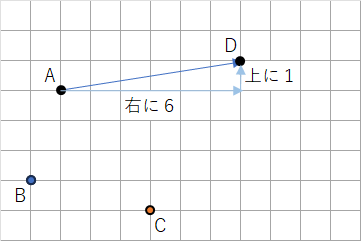
点Ｂと点Ｃも右に６マス、上に１マス移動させたら次のようになるよね。
点の移動ができたら、点を線で結べば、平行移動した△DEFの完成。
平行移動の練習問題① マス目がある問題
くまごろう移動した図を作図する問題には「マス目あり」と「マス目なし」があって、「マス目なし」の方が難しいよ。
（問１）
下の図の△ABCを矢印の方向に平行移動した△DEFを作図しなさい。
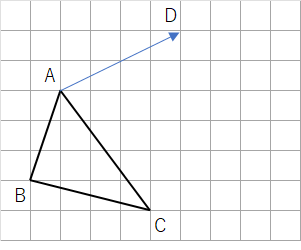
点Aから点Dに移動するまでに、右に４マス、上に２マスだよね。だから、点Bも点Cも同じように、右に４マス、上に２マス移動させてみよう。
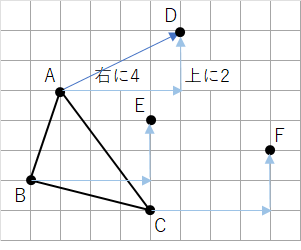
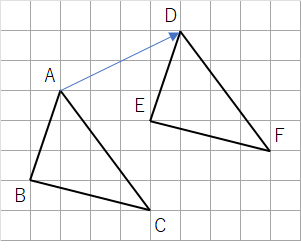
点の移動ができたら、点を線で結べば、平行移動した△DEFの完成だね。
平行移動の練習問題② マス目がある問題
（問２）
下の図の△ABCを矢印の方向に平行移動した△DEFを作図しなさい。
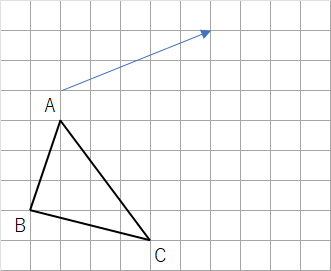
今までの問題と違うのは、矢印が点Aから離れていることだね。ただ、平行移動のやり方は変わらないよ。
矢印のスタート地点と終わりを確認すると、右に５マス、上に２マス動いているよね。だから、点Aと点Bと点Cを矢印と同じく右に５マス、上に２マス移動させてみよう。
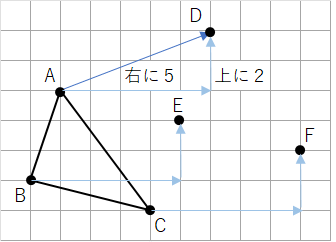
点の移動ができたら、点を線で結べば、平行移動した△DEFの完成だね。
たろう矢印が図形から離れたところにあるときは、少し難しくなるんだね。
平行移動の練習問題③ マス目がない問題
（問３）
下の図の△ABCを矢印の方向に平行移動した△DEFを作図しなさい。
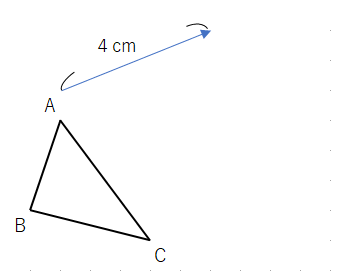
今までの問題と違うのは、マス目がないことだよね。だから定規やコンパスを使って作図しないといけないんだ。
作図の仕方
①点A、点B、点Cを通る矢印と平行な直線を引いてね。長さは適当で大丈夫だよ。定規２本使えば、平行な線が書けるよね。
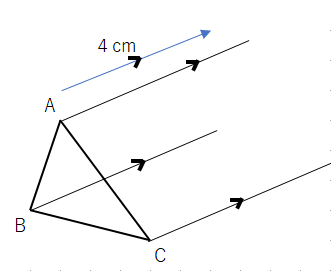
②コンパスで矢印の長さ（４cm）を広げよう。広げたあと、幅を変えないようにね。（定規で４cm測る方法もあるよ。）
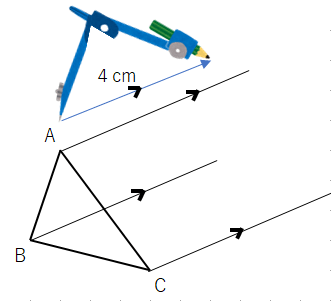
③コンパスの針を点Aにさして、さっき書いた平行な線に印をつけよう。（定規でやる人は、点Aから４cmのところに印）
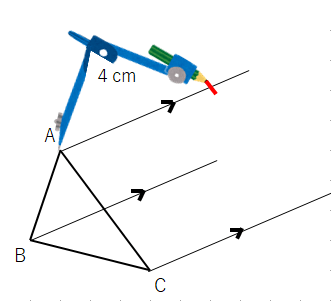
④コンパスを点Bにさして、さっき書いた平行な線に印をつけよう。（定規でやる人は、点Bから４cmのところに印）
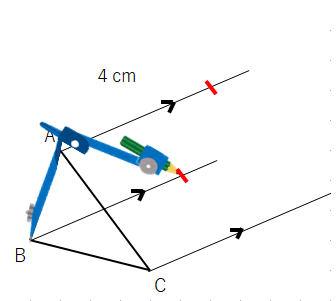
④コンパスを点Cにさして、さっき書いた平行な線に印をつけよう。（定規でやる人は、点Cから４cmのところに印）
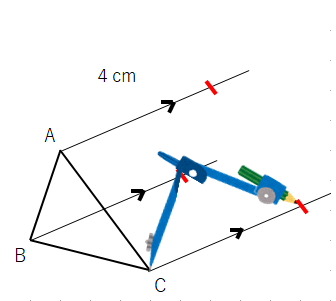
⑤印をつけたところが、点D、点E、点Fになるから、結んだら△DEFの完成だよ。
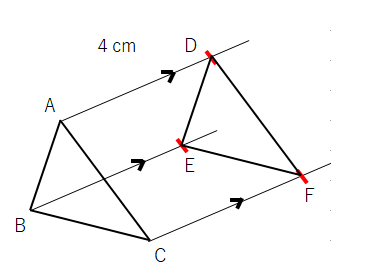
平行移動の特徴
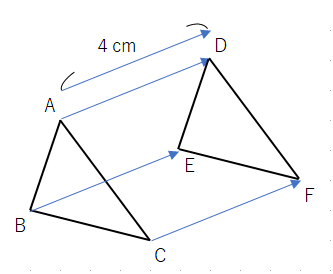
平行移動の特徴は次の通りだよ。
平行移動の特徴
対応する点を結んだ線分は平行で長さが等しい。
上の図形でいうと、矢印が平行で長さが等しいということになるよ。この関係を記号で書くと、AB＝DE、BC＝EF、AC＝DF、AB//DE、BC//EF、AC//DF。
ちなみに「//」という記号は「平行」という意味だよ。
回転移動とは
回転移動とは、ある点を回転の中心として、ある角度だけ回転させる移動のことだよ。
回転移動の例題
（例）
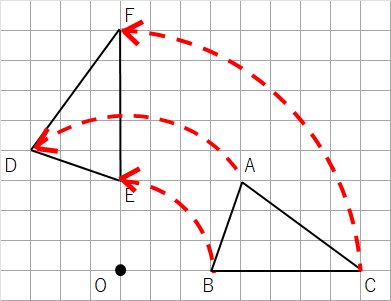
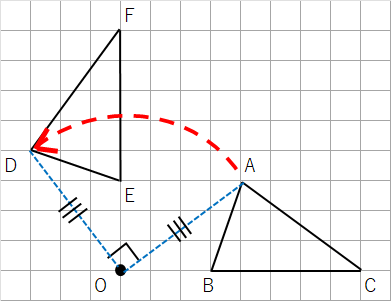
下の△ABCを点Oを回転の中心として反時計回りに９０°回転移動した△DEFを作図しなさい。
先に答えを見せるね。答えはこんな感じになるよ。
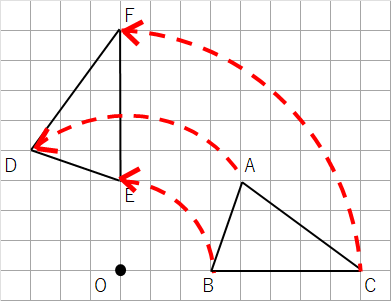
点Aを見ても、なぜ点Dの位置にきているかがわかりにくいけど、点Bと点Cならわかりやすいと思うよ。
点Bを見てみよう。点Bは反時計回りに９０°回転移動して点Eにきていることがわかるよね。
点Cを見てみよう。点Cは反時計回りに９０°回転移動して点Fにきていることがわかるよね。
回転移動の作図のやり方
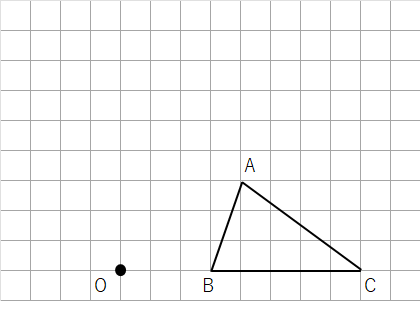
①回転の中心Oと点Aを結ぼう。
②点Oを通る線分OAに垂直な直線を引こう。
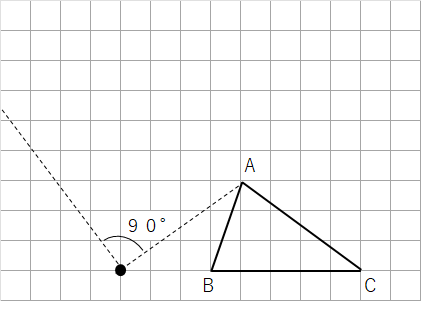
③回転の中心Oにコンパスの針をさして、線分OAの長さだけ広げよう。
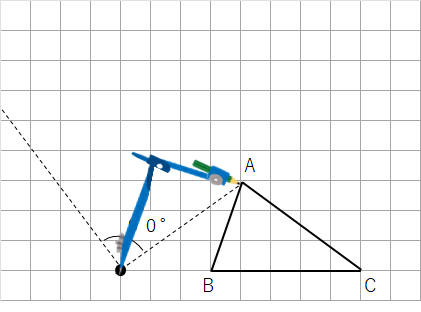
④コンパスをOにさした状態で、反時計回りにおよそ９０°以上回そう。
⑤「さっき書いた線分OAに垂直な直線」と「コンパスの線」が重なるところに印をつけよう。
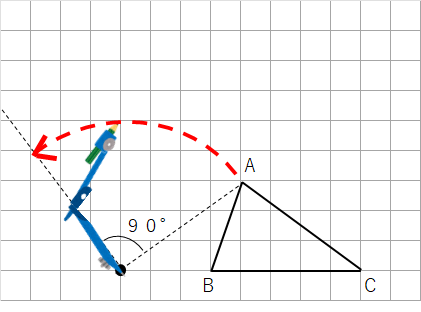
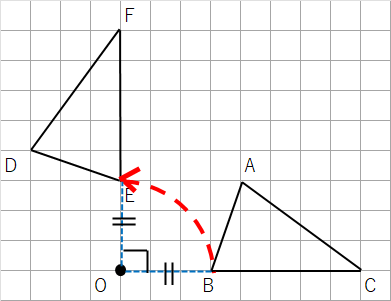
点Aと同じように点B、点Cをやっていこう。
⑥回転の中心Oと点Aを結ぼう。
⑦点Oを通る線分OBに垂直な直線を引こう。
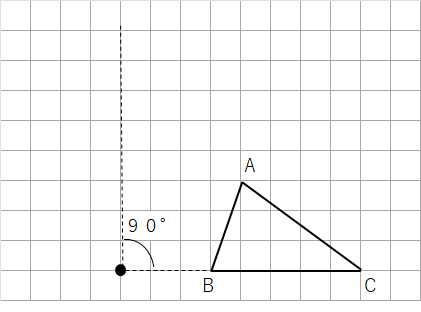
⑧回転の中心Oにコンパスの針をさして、線分OBの長さだけ広げよう。
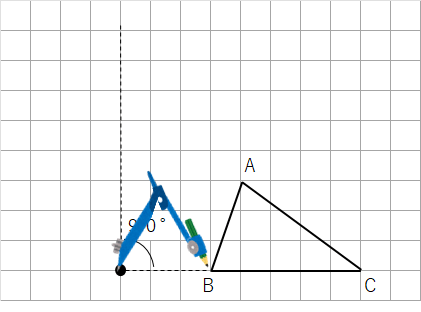
⑨コンパスをOにさした状態で、反時計回りにおよそ９０°回そう。
⑩「さっき書いた線分OBに垂直な直線」と「コンパスの線」が重なるところに印をつけよう。
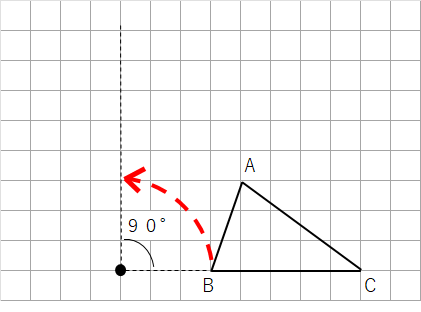
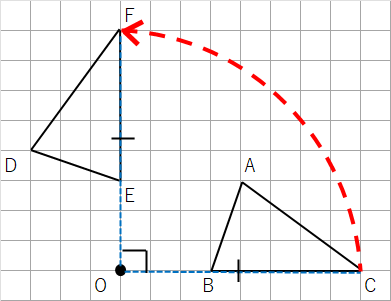
同じように点Cもやると次のようになるよ。
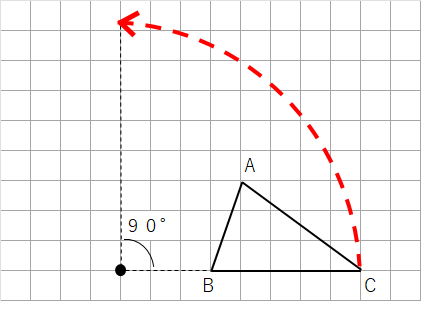
全部の点を反時計回りに９０°回転させることができたから、これで完成。答えは次のようになるよね。
この問題はマス目があるバージョンでやったけれど、なくても定規とコンパスを使えばできるよね。
くまごろう今回は反時計回りに９０°だったけど、「時計回り」や「６０°」「１２０°」とかもよく出る問題だからね。作図をする前にどっち周りに何度回すかはしっかり見ておこう。
回転移動の特徴
回転移動での点A、点B、点Cの移動の仕方は次の通りだよ。
回転移動の特徴
- ①対応する点は、回転の中心から等しい距離にある
→OA＝OD、OB＝OE、OC＝OF - ②対応する点と回転の中心でできる角はすべて等しい。
→∠AOD＝∠BOE＝∠COF＝９０°
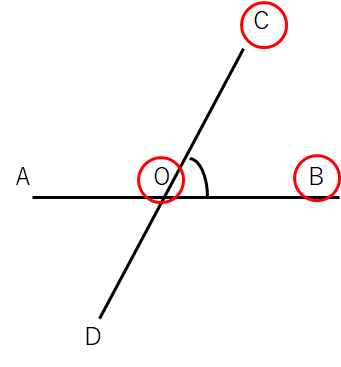
角の表し方
ちなみに「∠（かく）」という記号は「角」という意味だよ。いちいち、「角」という漢字を書いていたら大変だからね。
「角」「∠」を使うときに気をつけないといけないことがあるんだ。
下の図で印のついた角を言いたいとき、「∠O」といってもどこかわからないよね。だって、十字の右上も右下も左上も左下も「∠O」になるからね。
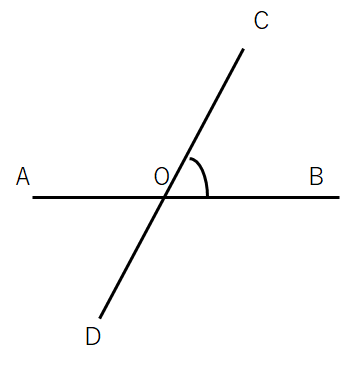
そんなときは「はさむ」。
印のついた角は「∠COB」と表すと１か所に決まるよ。
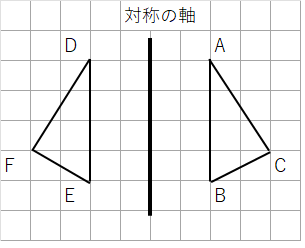
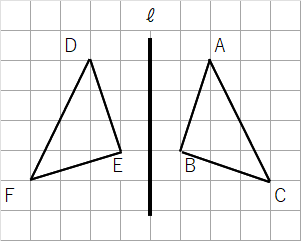
対称移動とは
対称移動とは、軸を折り目としたときにびったりと重なるように移動させることだよ。
下の図をみたら、対称移動がひと目で理解できるかな。
軸で折ったらぴったり重なるよね。多分３つの移動の中で一番簡単だと思うよ。
対称移動の特徴
対称移動の作図のやり方の前に特徴を考えよう。対応する点同士を結ぶと次のことがわかるよ。
対称移動の特徴
- 対称の軸ℓと対応する点同士を結んだ線分（赤線）は垂直に交わる。
→AD⊥ℓ、CF⊥ℓ、BE⊥ℓ - 対応する点同士を結んだ線分は、対称の軸ℓで二等分される。
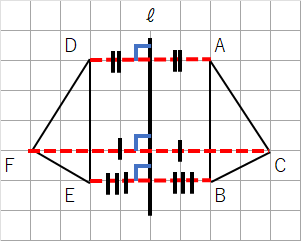
ちなみに「⊥」という記号は「垂直」という意味だよ。いちいち、「垂直」という漢字を書いていたら大変だからね。
対称移動の作図のやり方
（例）
下の△ABCを、直線ℓを対称の軸として対称移動した△DEFを作図しなさい。
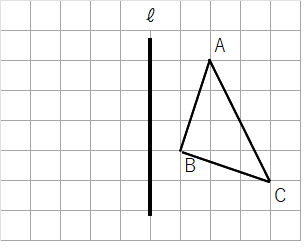
①点A、点B、点Cから直線ℓに対して垂直な直線を引こう。
②対称の軸から、点A、点B、点Cまでの長さと同じ分、反対側にとろう。
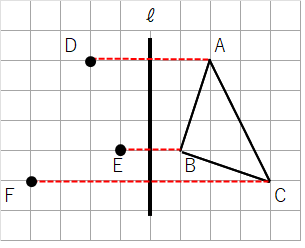
③最後に点D、点E、点Fを結んだら、対称移動した△DEFが完成。
垂直二等分線とは
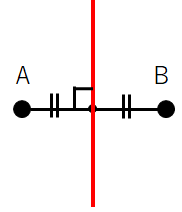
垂直二等分線とは、線分の中点（真ん中の点）を通り、線分に垂直な直線のことだよ。
例えば、線分ABがあったとしよう。
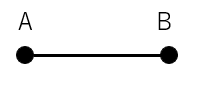
線分ABを二等分する点を中点といって、その中点を通って線分ABに垂直な直線を書くとこんな感じ。この赤線のことを垂直二等分線というよ。
運営者情報
ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。
-
わかりやすかったです(^▽^)/
わかりやすかったです(^▽^)/