「球の表面積の求め方」球の表面積の公式と覚え方をくわしく解説
中学数学で学習する「球の表面積」について、球の表面積はどうやって求められるのか、考え方や公式、公式の覚え方をくわしく解説するよ。
目次
球の表面積を調べてみよう
球の表面積って、どうやって求めたらいいんだろう？
面積は「底辺×高さ」で求めることができるけれど、丸くて平らなところもないし、直線もない球の場合だと、一体どうやって表面積を求めたらいいのかわからないよね。
「球の体積の公式」で学習したように、球の表面積も求めるための公式がちゃんとあって、それさえ覚えてしまえばある程度の問題は解けるようになるよ。
ただ、どうしてその公式が成り立つのか？を考えることで、少し発展的な問題も解けるようになるし、納得して公式を覚えることができるよね。
そこで、まずは「球の表面積」を求める考え方をくわしく説明していくよ。
球の表面積を、紐と円を使って調べてみよう。
「半径５cmの球」があるとするよ。
①この「半径５cmの球」のまわり全体にすき間なく、ひもを巻き付けてみるとするよ。
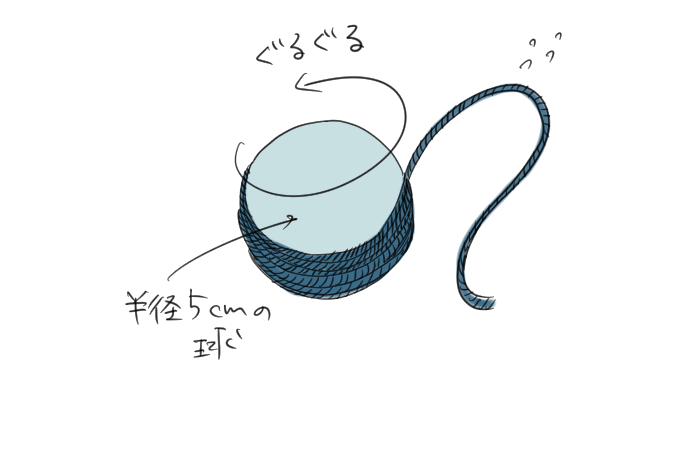
②次に、そのひもをほどいて、円になるように巻きなおしてみるとするよ。
なんと、ひもをほどくと、もとの球の半径である「５cm」の２倍の、「半径が１０cmの円」になるんだよ。
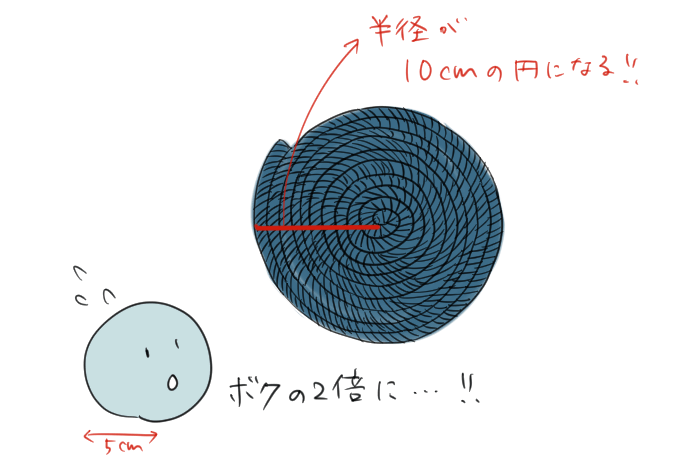
球の表面積と円の面積の関係
「半径ｒ(cm)の球の表面積」は「半径２ｒ(cm)の円の面積」と同じになる。
では、実際に「半径２ｒ(cm)の円の面積」はいくつになるか計算してみよう。
半径２ｒ(cm)の円の面積は
（半径）×（半径）×（円周率） ←円の面積の公式
＝２ｒ×２ｒ×π
＝４πｒ２
半径２ｒ(cm)の円の面積は４πｒ２(cm2)になることがわかったね。
「半径ｒ(cm)の球の表面積」は「半径２ｒ(cm)の円の面積」と同じになるから、半径ｒ(cm)の球の表面積は４πｒ２(cm2)だよ。
この「４πｒ2(cm2) 」が、円の表面積の公式なんだ。
円の表面積の公式
４πｒ2(cm2)
球の表面積と円柱の側面積の関係
半径がｒcmの球の表面積と、半径が２ｒcmの円の面積の関係はわかったかな。
では、今度は「球の表面積」と、「円柱の側面積」の関係を見てみよう。
古代ギリシャの数学者である「アルキメデス」という人が、「球の表面積と円柱の側面積」のある関係性を発見したんだ。
なんとアルキメデスが言うには、球の表面積は、その球がちょうど入る円柱の側面積に等しいということがわかったんだ。
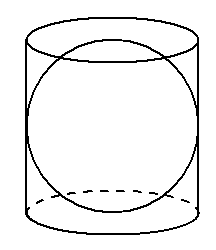
本当にそうなるのか、実際に計算して試してみよう。
半径ｒcmの球と、球がちょうど入る円柱を考えてみよう。
円柱の高さは球の直径になるから２ｒcmになるよね。
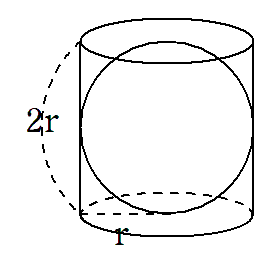
この円柱の側面積が、球の表面積と等しくなるのかどうか、円柱の側面積を求めてみよう。
①円柱の展開図を書こう。
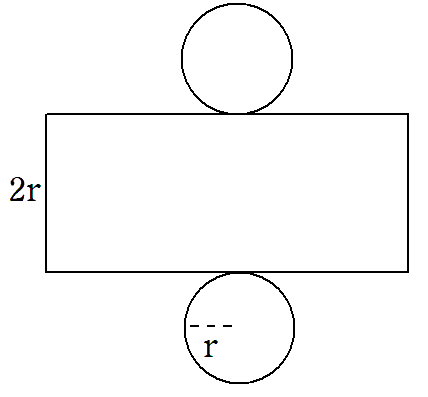
②側面の長方形の面積に注目しよう。
長方形の横の長さは、底面の円周と同じだったよね。
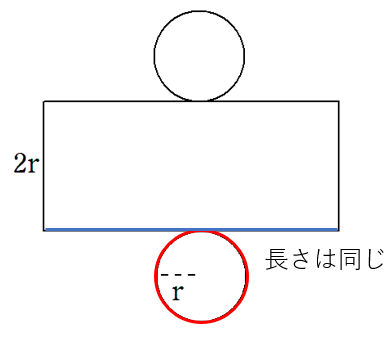
③底面の円周を求めてみよう
（直径）×（円周率） ←円の円周の長さを求める公式
＝２ｒ×π
＝２πｒ
底面の円周の長さが２πｒ(cm)と求めることができたね。だから、長方形の横の長さも２πｒ(cm)ってことだね。
④側面の長方形の面積を求めよう
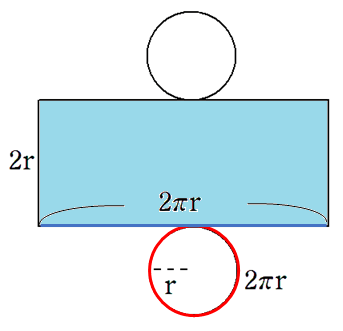
長方形の面積は次のようになるよ。
（たて）×（横）
＝２ｒ×２πｒ
＝４πｒ２
半径ｒcmの球がちょうど入る円柱の側面積は４πｒ２(cm2)になることがわかったね。
アルキメデスの発見
球の表面積は、その球がちょうど入る円柱の側面積に等しい。
球の表面積の求め方（球の表面積の公式）
球の表面積を求める公式は次のようになることがわかったね。
球の表面積の公式
半径ｒの球の表面積をＳとすると
Ｓ＝４πｒ２になる。
この公式を使って、実際に問題に挑戦してみよう。
問１
半径３cmの球の表面積を求めなさい。
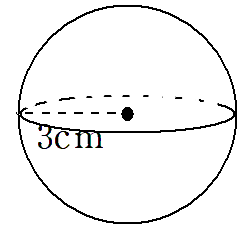
球の表面積を求める公式は
Ｓ＝４πｒ２だから、半径ｒ＝３を代入すると
＝４π×３２
＝４π×９
＝３６π
球の表面積は３６π(cm2)と求めることができたね。
問２
半径３cmの半球の表面積を求めなさい。
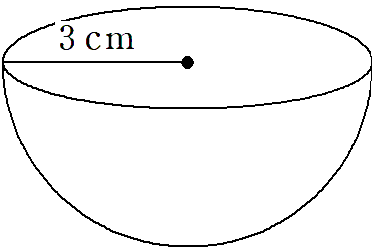
球の半分の半球の表面積を求める問題には注意が必要だよ。とりあえず、球の表面積を求めて、それを半分にしてみよう。
半径３cmの球の表面積は
S＝４πｒ２だから、半径ｒ＝３を代入すると
＝４π×３２
＝４π×９
＝３６π
球の表面積は３６π(cm2)と求めることができたね。
問題は「半球」だから、まずは半分にしよう。
３６π÷２＝１８π。
ただ、この１８π(cm2)っていうのは、図の「黄色で塗った部分」の面積しか考えていなんだ。
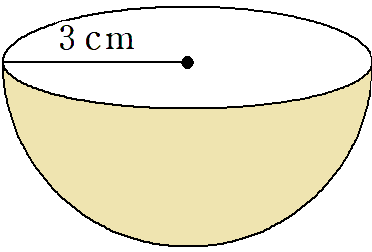
「表面積」と言ったら、空気に触れているところのことだから、水色の部分も考えないといけないよね。
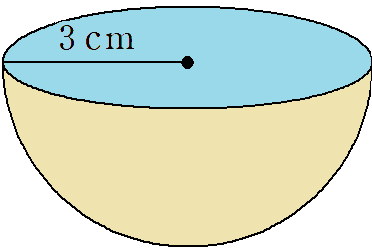
水色の部分は、普通に円の面積を求めればいいね。
水色の円の面積は３×３×π＝９πだから、これにさっき求めた１８πを足して、「半球の表面積」の答えは９π＋１８π＝２７π(cm2)になるよ。
球の表面積の公式の覚え方（語呂合わせ）
球の表面積の公式は４πｒ２だったよね。実は体積と同じように語呂合わせで覚えることができるんだよ。
語呂合わせ
・しんぱい あーるにじょう
（４π） （ｒ２）
・しんぱい あるある
（４π） （ｒ×ｒ）
「球（急）の表面積（表面上）」は「心配あるある」ということで、
急なセールスが来て、表面上はニコニコしているけれど、騙されるんではないかと心配しているイメージはどうかな笑。
運営者情報
ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。
