円錐の表面積の求め方を解説(裏ワザあり)「立体の表面積」
中学校1年生の数学で学習する、立体の表面積の求め方について、円錐の表面積の求め方のポイントをわかりやすく解説しているよ。
例題もあるので、円錐の表面積の求め方の流れがよくわかるよ。
また、求めるのが複雑な円錐の表面積をカンタンな計算で求める方法(裏ワザ)も紹介するよ。
円錐の表面積の求め方
それでは、今度は「円錐」の表面積の求め方を解説していくよ。
次の図のような円錐の表面積を考えよう。
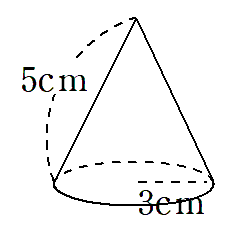
円錐の表面積も、やっぱり1回で求められるような公式はないんだ。
円柱の表面積を求めた時と同じように底面積と側面積で分けて考えよう。
円錐の底面積を求めよう
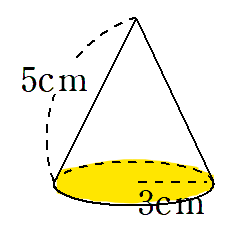
上の円錐の底面は半径3cmの円だから、
(半径)×(半径)×(円周率) ←円の面積を求める公式
=3×3×π
=9π
円錐の底面積は9πcm2ってことがわかったよね。次は側面積を求めるよ。
円錐の側面積を求めよう
円錐の側面積も、求めるのはちょっと大変なんだけれど、ひとつずつ確認していこう。
円錐の側面積の求め方を考えるために、円錐の展開図を見てみよう。
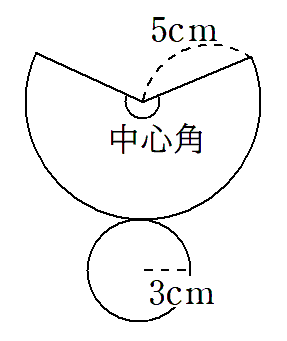
円錐の側面は、展開図の「おうぎ形」の部分だよね。
なので、円錐の側面積=おうぎ形の面積になるね。
おうぎ形の面積を求める公式を復習しよう。
(おうぎ形の面積)
=(半径)×(半径)×(円周率)×\(\frac{中心角}{360}\)
この公式に当てはめていくと、「半径」は、円錐の母線と同じだから、5cmとわかるんだけれど、「中心角」がわからないね。
円錐の側面おうぎ形の中心角を求める
おうぎ形の中心角を求めるために、下のようにおうぎ形をふくむ円を考えてみよう。
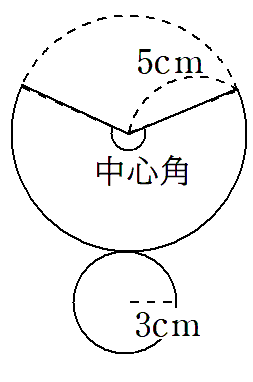
上の図を色分けして考えるとわかりやすいと思う。
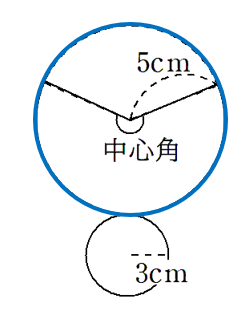
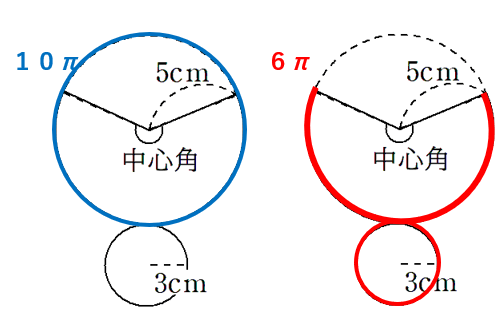
青色で表した円の円周は
(直径)×(円周率)
=10×π
=10π
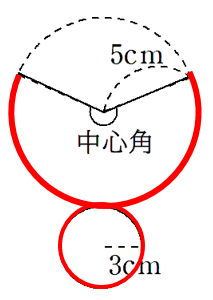
赤色で表したおうぎ形の弧の長さは、底面の円周と同じだから
(直径)×(円周率)
=6×π
=6π
まとめると、次のようになるよ。
中心角を求めるんだけど、1周って360°だったよね。青色が1周分の長さで、赤色が中心角分の長さだから、次のような式で円周角を求められるよ。
360×\(\frac{赤}{青}\)
=360×\(\frac{6π}{10π}\)
=216°
中心角が216°ってわかったから、おうぎ形の面積は
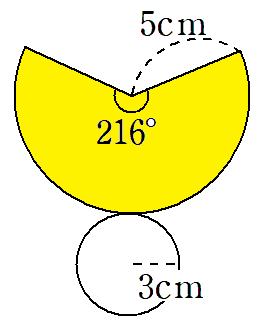
(半径)×(半径)×(円周率)×\(\frac{中心角}{360}\)
=5×5×π×\(\frac{216}{360}\)
=25π×\(\frac{3}{5}\)
=15π
円錐の側面のおうぎ形の面積は15πcm2になることがわかったね。最後に円錐の表面積を求めよう。
円錐の表面積

底面積が9πcm2、側面積が15πcm2になるから、表面積は次のように求めるよ。円錐は、底面が1つしかないから、底面積と側面積を足すだけでいいね。
(底面積)+(側面積)
=9π+15π
=24π
円錐の表面積が24πcm2と求めることができたね。
円錐の表面積の求め方 ポイントまとめ
・表面積=「底面積」と「側面積」でわけて求める。
・側面のおうぎ形の中心角を求める。
・側面のおうぎ形の弧の長さと、底面の円の円周の長さは等しい。
円錐の表面積を求める問題
次の円錐の表面積を求めなさい。
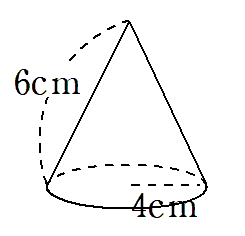
底面積を求めよう
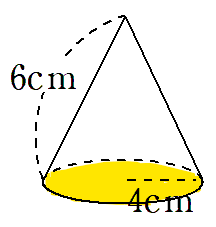
上の円錐の底面は半径4cmの円だから、
(半径)×(半径)×(円周率) ←円の面積を求める公式
=4×4×π
=16π
円錐の底面積は16πcm2になるね。
側面積を求めよう
円錐の側面はおうぎ形になるんだったよね。円錐の展開図を書いてみよう。
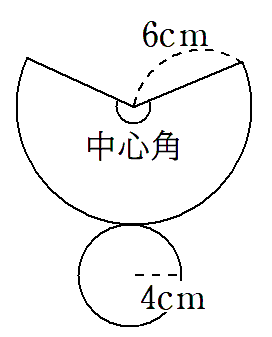
おうぎ形の中心角を求めるために、おうぎ形をふくむ円を考えてみよう。
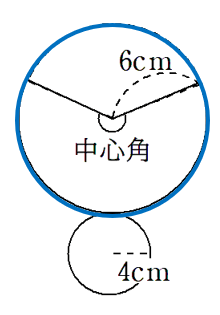
青色で表した円の円周は
(直径)×(円周率)
=12×π
=12π
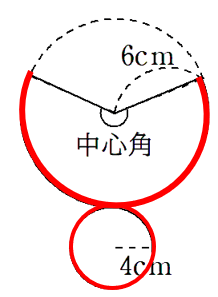
赤色で表したおうぎ形の弧の長さは、底面の円周と同じだから
(直径)×(円周率)
=8×π
=8π
まとめると、次のようになるよ。
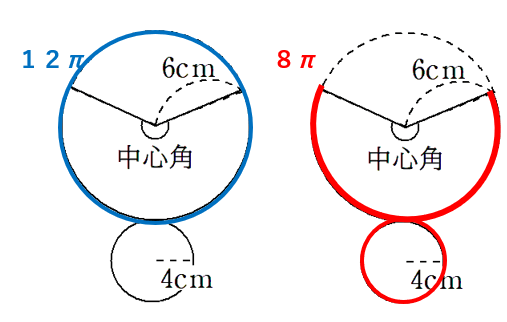
中心角を求めるんだけど、1周って360°だったよね。青色が1周分の長さで、赤色が中心角分の長さだから、次のような式で円周角を求められるよ。
360×\(\frac{赤}{青}\)
=360×\(\frac{8π}{12π}\)
=240°
中心角が240°ってわかったから、おうぎ形の面積は
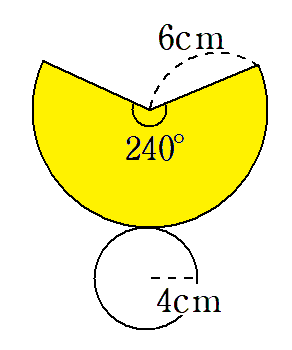
(半径)×(半径)×(円周率)×\(\frac{中心角}{360}\)
=6×6×π×\(\frac{240}{360}\)
=36π×\(\frac{2}{3}\)
=24π
円錐の側面のおうぎ形の面積は24πcm2になることがわかったね。
表面積を求めよう

底面積が16πcm2、側面積が24πcm2になるから、表面積は次のように求めるよ。
(底面積)+(側面積)
=16π+24π
=40π
円錐の表面積が40πcm2と求めることができたね。
円錐の側面積を求める裏ワザ
円錐の側面積を求めるのってすごく面倒だよね。ただ、こんな裏ワザがあるんだ。
円錐の側面積を求める裏ワザ
(円錐の側面積)=(母線)×(半径)×(円周率)

さっきの問題であれば、母線が6cm、半径4cmだから
(母線)×(半径)×(円周率)
=6×4×π
=24π
側面積が24πcm2って一瞬で求まったね。知っておくと便利かもしれないね。
運営者情報

yumineko
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。

-
-
側面積は母線×半径×πの方がわかりやすいですよ。
-
側面積は母線×半径×πの方がわかりやすいですよ。
-
中一の復習をしたかったので助かりました!
本当にありがとうございます!




すごく分かりやすくて助かりました。
ありがとうございます。