一次方程式とは?「解」と「等式の性質」をわかりやすく解説
中学1年生の数学で学習する「方程式」について、方程式とはなにか、一次方程式とはどういうことか、「解」とはなにか、等式の性質とはどういうもので、どのように使うのか?をわかりやすく解説するよ。
方程式とは
 教科書
教科書方程式をひとことで言うと、「正体不明の文字が入っている等式」。
「等式」とは何かは、「文字式の利用」について解説しているページでも説明したね。そう、「=(イコール)」で結ばれた式のことだったね。
つまり、○○=✖✖という形の式のこと。
この等式に、文字が入ったものを、まず「方程式」と呼ぶんだ。
教科書が言っている「xの値によって、成り立ったり、成り立たなかったり」という部分は、つまりは「xという文字が使われているよ」というイメージで考えてOK。
そうすると「xという文字が使われている方程式を、xについての方程式という」というごく当たり前のことを言っているだけだね。
「一次方程式」とは?
方程式がなにかは分かったけれど、では「一次方程式」ってなんだろう?
数学では、式の中で、掛け合わされている文字の個数のことを「次数」と呼ぶんだ。つまり、式の中に、文字が何個「かけられているか」の数。
たとえば、「x=4」という式だったら、「x」は1つだけだよね。
これをちょっとややこしいけれど、「1つだけ”かけられている”」と考えてあげてね。
そうすると、この式は「一次」の式になるんだ。
では、「xy=8」という式はどうだろう。
「x」と「y」の2つの文字がかけられているね。
だから、これは「2次」の式だよ。
「x2=16」はどうかな?
「x2」は、「x」に「x」をかけたものだよね。
だから、2つのx(2つの文字)がかけられているから、これも「2次」の式だよ。
ここで注意したいのが、「x+y=8」というような式。
これも、2つの文字が登場しているから、「2次なのかな?」と思ってしまうよね。
でも、これは「x」と「y」は「かけられてはいない」よね。足されているだけ。
だから、これは「x」も「y」も、それぞれ「1つの文字がかけられている」と考えるから、「1次」の式なんだ。
そして、式の「次数」は、その式の中にある一番多い次数で呼ぶんだ。
たとえば、「x+xy=12」なんて式があったとするよ。
「x」は1次だね。「xy」は2次だよね。
そうすると、一番多い次数は「2次」だよね。
そのとき、この式は「2次の式」と呼ぶんだ。
たとえば「次数」のことは「レベル」だとイメージしてみて。
辛さレベルが「1~3」まであるカレー屋さんのメニューがあったとして、
「辛さレベル1のチキンカレーと辛さレベル3のエビカレー」のセットは、きみだったらどの辛さレベルのページに載せる?
辛さレベル「1」のページに載せるわけにはいかないよね。
より辛いほうの「レベル3」のページに載せるんじゃないかな?
数学でも、次数が多くなるほど複雑な式になるんだから、その式の中の一番多い次数で呼んでおこうね、ということなのかもしれないね。
1年生では、x2とかがでてこない、最高次数が「1」の一次の方程式を学習するんだ。それが「一次方程式」だよ。
方程式の例題
さて、方程式のことは分かったけれど、じゃあ、結局「方程式で何するの?」ってなるよね。
これからの学習では、「方程式を解く」ということをするんだ。
方程式は、文字が使われている等式だよね。
文字って、いくつの数字なのか、正体が不明だよね。
その文字の正体を見つけちゃおう!!ということ。
例えば、次の問題を考えてみよう。
(例1)方程式x+4=5は、xにいくつを入れると成り立つかな?
ぱっとわかる人はいいんだけど、わからない人はxに順番に数字を入れてみよう。xに0~4まで入れてみたよ。左辺と右辺の値が同じになる(これを「方程式が成り立つ」というよ)のは、xがいくつのときかな?
| xの値 | 左辺 x+4 | 大小関係 | 右辺 5 |
| x=0 | 0+4=4 | < | 5 |
| x=1 | 1+4=5 | = | 5 |
| x=2 | 2+4=6 | > | 5 |
| x=3 | 3+4=7 | > | 5 |
上の表から、xが1のとき、左辺と右辺が同じになって、方程式が成り立つね。
方程式の解とは
方程式を成り立たせることができる、xの正体「1」を見つけることができたね。
 くまごろう
くまごろう「解」は、「問題の答え」という意味があるよ。
つまり、方程式の「答え(文字の正体)」ということだね。
方程式x+4=5の解はx=5になるよ。
(例2)方程式x-5=-3の解を求めなさい。
ぱっとわかる人はいいんだけど、わからない人はxに順番に数字を代入してみよう。xに0~4まで代入してみたよ。左辺と右辺の値が同じになるのは、xがいくつのときかな?
| xの値 | 左辺 x-5 | 大小関係 | 右辺 -3 |
| x=0 | 0-5=-5 | > | -3 |
| x=1 | 1-5=-4 | > | -3 |
| x=2 | 2-5=-3 | = | -3 |
| x=3 | 3-5=-2 | < | -3 |
| x=4 | 4-5=-1 | < | -3 |
上の表からx=2のときに、左辺と右辺が等しくなるから、x=2が解になることがわかるね。
 くまごろう
くまごろう(例3)方程式2x-4=xを解きなさい。
この問題は、さすがにぱっとわかる人は少ないんじゃない?今までの2問と何が違うかっていうと、右辺にも「x」があるってことだね。
だから下の表で考えてみよう。
| xの値 | 左辺 2x-4 | 大小関係 | 右辺 x |
| x=0 | 2×0-4=-4 | < | 0 |
| x=1 | 2×1-4=-2 | < | 1 |
| x=2 | 2×2-4=0 | < | 2 |
| x=3 | 2×3-4=2 | < | 3 |
| x=4 | 2×4-4=4 | = | 4 |
上の表からx=4のときに、左辺と右辺が等しくなるから、x=4が解になることがわかるね。
方程式で出てくる用語
方程式では次の言葉が出てきたよ。もう一度しっかり確認して覚えよう。
方程式で出てくる用語
①方程式
- xの値によって、成り立ったり、成り立たなかったりする式のこと
- 「方」は「左右」、「程」は「大小の比較」という意味があるため、「方程」とは左右をの大小の比較をすることが由来になっているよ。
②一次方程式
- 文字(xなど)の最高次数が「1」である方程式
- 1年生で学習する方程式
※3年生で、二次方程式っていうのを勉強するよ。(x2+3x+2=0)
③方程式の解
- 方程式を成り立たせるxの値のこと
- 方程式の左辺と右辺の値を等しくするxの値
④方程式を解く
- 方程式の解を求めること
方程式の練習問題
方程式の基本がわかったところで練習問題を2問やってみよう。
(問1)方程式2x+5=11の解は1、2、3のうちどれか。
 たろう
たろうx=1のときを考えよう。
(左辺)=2×1+5=7 (右辺)=11 → 7と11だから違うな。
x=2のときを考えよう。
(左辺)=2×2+5=9 (右辺)=11 → 9と11だから違うな。
x=3のときを考えよう。
(左辺)=2×3+5=11 (右辺)=11 → 両方11だ!ということはx=3が解だね。
(問2)次のア~エの方程式のうち、解が-2であるものはどれかな?
ア:3x+2=8 イ:x-5=3
ウ:-2x=4 エ:2x-3=x-1
 たろう
たろう答えを先にいうと・・・ウが正解だよ。他のやつはx=-2では等式が成り立たないよ。実際に代入して確かめてみよう。
ア:3x+2=8にx=-2を代入しよう。
(左辺)=3x+2
=3×x+2
=3×(-2)+2 ←マイナスを代入するときは( )をつけよう
=-6 +2
=-4
(右辺)=8
→-4と8だから違うな。
イ:x-5=3にx=-2を代入しよう。
(左辺)=x-5
=(-2)-5
=-7
’(右辺)=3
→-7と3だから違うな。
ウ:-2x=4にx=-2を代入しよう。
(左辺)=-2x
=-2×x
=-2×(-2)
=4
(右辺)=4
→両辺が4になったから、この問題は解が-2になる。
エ:2x-3=x-1にx=-2を代入しよう。
(左辺)=2x-3
=2×x-3
=2×(-2)-3
=-4-3
=-7
(右辺)=x-1
=(-2)-1
=-3
→-7と-3で違うな。
 たろう
たろう実はもっと簡単に解を求める方法があるんだ。
その方法は次の「方程式の解き方」を解説するページで説明するんだけれど、その学習をする前に、「等式の性質」のことを知っておく必要があるんだ。
等式の性質とは
方程式を簡単に解くために、必要な知識が「等式の性質」。
等式の性質は次の通りだよ。
等式の性質
等式は左辺・右辺の両方に同じ数を「たしても・ひいても・かけても・わっても」、等式は成り立ったまま。
等式の性質が成り立つ理由
 くまごろう
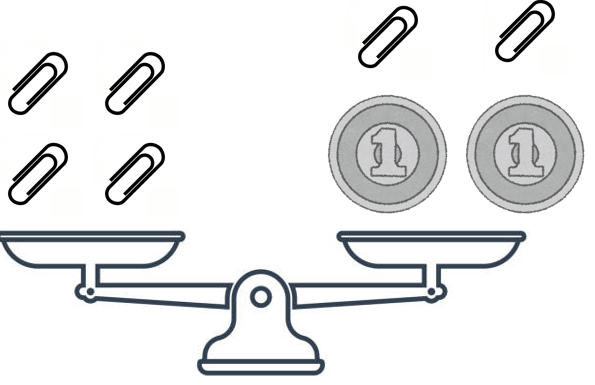
くまごろう1円玉とクリップの重さをてんびんで考えてみよう。下のようになっていたら、「クリップ4個」=「1円玉2枚とクリップ2個」の重さは等しいってことだよね。
式にしたら、「4クリップ=1円2枚+2クリップ」みたいな感じ。
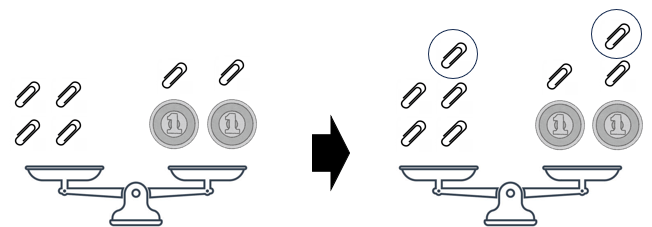
左辺・右辺の両方に同じ数を「たしても」よい理由
てんびんの両方にクリップ1枚を置くよ。左右の重さが変わらないことがわかる?当たり前だよね。両方に同じものを乗っけているんだから。
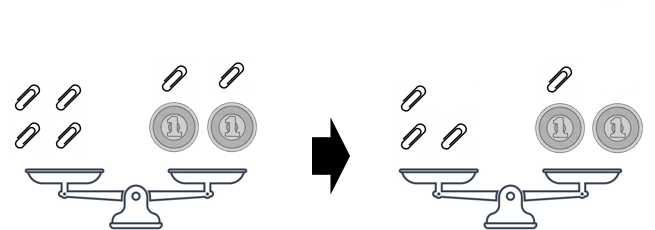
左辺・右辺の両方に同じ数を「ひいても」よい理由
じゃあ、両方からクリップ1枚を減らすよ。左右の重さが変わらないことがわかる?同じ重さのものを左右から取っているから、重さは変わらないようね。
左辺・右辺の両方に同じ数を「かけても」よい理由
じゃあ、両方を2倍してみると、
左はクリップ4個だから8個になるよ。
右はクリップ2個と1円2枚だから、クリップ4個と1円4枚になるよ。
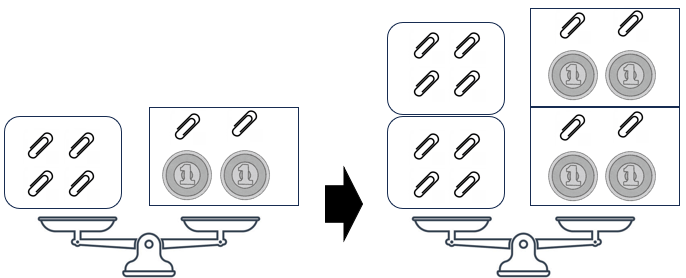
左の図で○と□が等しいから、右の図で○○と□□は等しくなることがわかるかな?
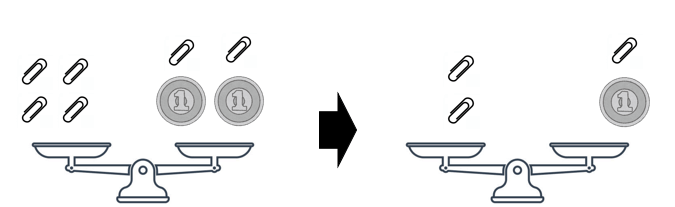
左辺・右辺の両方に同じ数で「わっても」よい理由
両方を2で割ってみるよ。
左はクリップ4個だから2個になるね。
右はクリップ2個と1円2枚だから、クリップ1個と1円1枚になるね。
等式の性質のまとめ
等式の性質
等式は左辺・右辺の両方に同じ数を「たしても・ひいても・かけても・わっても」、等式は成り立ったまま。
きちんとした教科書通りの表現で書くなら次の通りになるよ。
①等式の両辺に同じ数や式mを加えても、等式は成り立つ。
A=Bならば、A+m=B+m
②等式の両辺から同じ数や式mを引いても、等式は成り立つ。
A=Bならば、A-m=B-m
③等式の両辺に同じ数mをかけても、等式は成り立つ。
A=Bならば、Am=Bm
④等式の両辺を同じ数m(mは0でない)で割っても、等式は成り立つ。
A=Bならば、A÷m=B÷m
まとめ
「方程式とは何か」
「等式の性質」についてわかったかな?
方程式を簡単に解くためには等式の性質が必要になるから、しっかり覚えよう。
今回学習したことを下にまとめるね。
今回学習したことまとめ
- xの値によって、成り立ったり、成り立たなかったりする式のことをxについての方程式という。
- 方程式を成り立たせるxのことを、方程式の解といい、解を求めることを方程式を解くという。
- 方程式の解を求めるには、xに数を代入して、等式が成り立つかを調べればよい。
- 等式の性質を使うことで、簡単に方程式の解を求められる。
- 等式は左辺・右辺の両方に同じ数を「たしても・ひいても・かけても・わっても」、等式は成り立ったまま。
運営者情報

yumineko
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。




