「文字を使った式の問題」解き方を解説（パターン７つ）

中学数学「文字の使用」で学ぶ「文字を使った式」の問題の解き方を、７つの問題パターンごとに文字式の作り方からくわしく説明。

「文字を使った式の問題」解き方を解説（パターン７つ）のPDF（9枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次【本記事の内容】

1.文字を使った式とは
2.パターン①たし算や引き算を使って表す
3.パターン②かけ算やわり算を使って表す
4.パターン③２つの文字が登場する
5.パターン④図形の面積を表す
6.パターン⑤異なる単位のものを揃える
7.パターン⑥割合を表す
8.パターン⑦速さ・時間・道のりの関係を使う
8.まとめ

文字を使った式とは

なんのために文字を使った式なんて勉強するの？

これから方程式というのを勉強するのに、「いろいろな数量」を簡単に文字でシンプルに表さなきゃいけなくなるから。

ザックリいうと
「文章」を、「文字と数字と記号と単位だけ」にすればいい

くまごろう

では早速やってみるよ。

文字を使った式のつくり方（基本）

例えば、80円のチョコレートを\(x\)個買ったときの金額を、「文字と数字、記号と単位」だけで表してみよう。

ポイントは、「それぞれの数字や文字が、どういう関係か」 を考えるんだ。

もし3個買った場合の値段は、\(80×3\)で求められるよね。
つまり、チョコレートひとつの値段の「80円」に買った数をかけると、金額がわかる関係。

\(x\)個買ったときもこの関係に当てはまるから、\(x\)個買った時の金額は、

\(80×x\) 円

になるね。

これで「数字（\(80\)）」と、「文字（\(x\)）」と、「記号（\(×\)）」と「単位（円）」だけになったね。

でもここで、ルールが3つあるんだ。

文字を使った式を作るときのルール3つ

①掛け算は「\(×\)」を省略する。
例：\(80×x\)は　\(80x\)

②文字と数では、数のほうを先に書く。
例：\(x80\) ではなく、\(80x\)

③割り算は、分数を使って表す。
例：\(80÷x\)ではなく、\(\frac{80}{x}\)

ところで、割り算が分数になるのって、いまいちピンと来ないんだけど・・

「割り算＝分数」がピンと来ない場合は読んでみよう

例えば、1枚のピザを2人で分けたら、半分になるよね。

半分って、\(\frac{1}{2}\)だよね。
\(\frac{1}{2}\)というのは、「1（つのもの）を、2で分ける（割る）」という意味なんだよ。

この「割り算を分数で表す」というのは、とても重要なワザなので、絶対にマスターしてね！！！

このルールを守って、\(80×x\)の「\(×\)（かける）」は省略して、数字である\(80\)は文字の\(x\)よりも前に書くから、
\(80x\) 円
になるんだ。

\(80x\)というのは、\(80×x\)のことなんだね。

くまごろう

こうやって、「ことばで表されるいろいろな数量」を、文字を使ってルールを守りながら「数字と文字と記号と単位だけで表す」というのがここで学習する内容だよ。

いろいろな数量を文字をつかった式で表すんだけど、よく出るパターンが7つあるよ。
それぞれ例をチェックしてみよう。

パターン①たし算や引き算を使って表す

たし算の関係

例：「\(50\)ページまで読んだ本を、さらに\(x\)ページ読んだ時の読み終わったページ数」

関係は？
\(50\)ページに、\(x\)ページを加えればよい

答え：\(50＋x\) ページ

引き算の関係

例：「\(600\)円から\(x\)円を使ったときの残金」

関係は？
\(600\)円から使った\(x\)円を引くと、残金が求められる。

答え：\(600−x\) 円

パターン②かけ算やわり算を使って表す

かけ算の関係

例：「\(80\)円のチョコを\(x\)個買った時の金額」

関係は？
金額は、\(80\)円\(×\)買った数

\(80×x\) 円
でも「\(×\)（かける）」は省略するので、
答え：\(80x\) 円

わり算の関係

例：「\(120\)個のチョコを、クラス\(x\)人で分けたときの1人あたりのチョコの数」

関係は？
\(120\)個を、分ける人数で割る

\(120÷x\) 個
だけど「割る」は分数で表すので、
答え：\(\frac{120}{x}\) 個

パターン③２つの文字が登場する

例：「\(80\)円のチョコ\(x\)個と、\(100\)円のジュース\(y\)本を買ったときの金額」

関係は？
\(80\)円\(×\)買った数と、\(100\)円\(×\)買った数を加える

答え：\(80x＋100y\) 円

パターン④図形の面積を表す

例：「底辺が\(x㎝\)で、高さが\(y㎝\)の平行四辺形の面積」

関係は？
平行四辺形の面積の求めかたは「底辺\(×\)高さ」

答え：\(xy\) ㎠

例2：「底辺が\(x㎝\)で、高さが\(y㎝\)の三角形の面積」

関係は？
三角形の面積のもとめかたは「底辺\(×\)高さ\(÷2\)」

答え：\(\frac{xy}{2}\) ㎠

パターン⑤異なる単位のものを揃える

例：「\(x\) km進んで、さらに\(y\)m進んだ時の、進んだ距離の合計」

関係は？
それぞれの進んだ距離を足す。
だけど、\(x\)は「km」で、\(y\)は「m」だから、単位を揃えなければいけない。

くまごろう

そのまま「\(x＋y\)」なんてしてしまうとダメだよね。
1km＝1000mだから、\(x\)は\(y\)の1000倍だね。
だから\(y\)をそのままにして、\(x\)だけ1000倍すればいいよ。

答え：\(1000x＋y m\)

※または\(y\)は\(x\)の1000分の1と考えて\(x＋0.001y\)でもよいよ。
さらに、\(0.001\)は1000分の\(1\)のことだから、\(x＋\frac{y}{1000}\) ㎠でもよい。

パターン⑥割合を表す

くまごろう

「割合」という言葉や「%」が登場すると「難しい！」と拒否反応が出てしまう子が多いけれど、よく出る問題だから頑張ろう。

例：「\(x\)人いるクラスで、サッカー部に入っているのはそのクラスの5%だったとき、その人数」

関係は？
\(x\)の5%が求める人数。

5%というのは、分数で表すと\(\frac{5}{100}\)。
ということは、\(x\)に\(\frac{5}{100}\) をかければいい。

だから答えは\(\frac{5}{100}\)\(x\) 人。

※または、5%は「\(0.05\)をかける」でもよいので、
\(0.05x\) 人　でもOK。

%ではなく、「○割」と聞かれた場合は？

1割は10%のこと。
1.5割なら15%で、2割なら20%だね。

あとは同じように%を分数や少数に直して計算しよう。

パターン⑦速さ・時間・道のりの関係を使う

例：「\(x\)kmを\(40\)分で歩いたときの速さ」

速さ・時間・道のりの問題は、「み・は・じ」の関係を覚えていれば大丈夫！

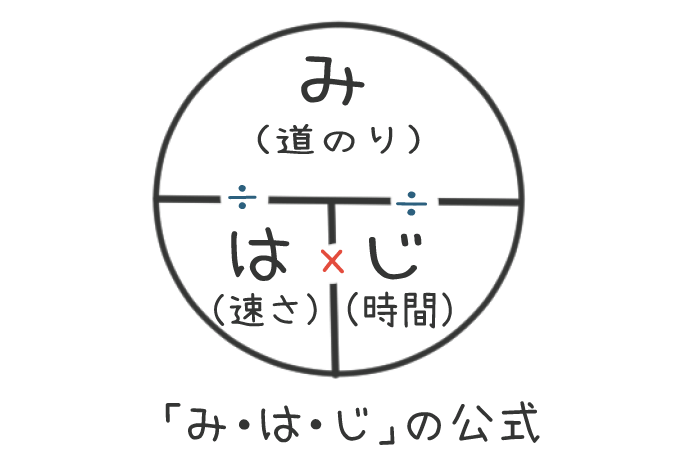
道のりと速さと時間の公式「みはじの公式」のイラスト

関係は？
道のりを時間で割ると速さが求められる。

\(x÷40\)
「\(÷\)」を分数で表すので、

答え：\(\frac{x}{40}\) km／分

例2：「時速\(5\)kmで\(x\)時間走った時の道のり」

関係は？
速さと時間をかけると道のりが求められる。

\(5×x\)
「\(×\)」を省略するので、
\(5x \)km

例3：「\(x\)kmを分速\(100\)mで走る時にかかる時間」

関係は？
道のり割る速さで、時間が求められる。

でもここで注意するのが、「単位が揃っているかどうか」。

kmとmが混ざっているね。
ということは、どちらかに揃えないといけないね。

1km＝1000mなので、\(x\)を1000倍するよ。
（または100mを1000で割る）

\(1000x÷100\)
「\(÷\)」は分数で表すので、
\(\frac{1000x}{100}\)
約分して、答えは\(10x\) 分

「文字を使った式の作り方」まとめ

まとめ

いろいろな数量は、文字を使って表す
ルール①掛け算は省略する
ルール②割り算は分数で表す
ルール③数字と文字では、数字が前になる
作り方パターン①たし算や引き算を使う
例：50ページ読んだ本を毎日5ページずつ\(x\)日読む→\(50＋5x\)
例：600円から\(x\)円使う→\(600ーx\) 円
パターン②かけ算や割り算を使う
例：80円を\(x\)個→\(80x\)円
例：120個を\(x\)人で→\(\frac{120}{x}\)個
パターン③文字を2つ使う
例：80円のチョコ\(x\)個と、100円のジューズ\(y\)本の金額→
\(80x＋100y\)円
パターン④図形の面積を表す
例：長方形など→底辺\(x\)㎝かける高さ\(y\)㎝→\(xy\)㎠
例：三角形など→ 底辺\(x\)㎝かける高さ\(y\)㎝\(÷2\) →\(\frac{xy}{2}\)㎠
パターン⑤単位を揃える
例：\(x\)kmと\(y\)m→
1km＝1000mなので、\(x\)を1000倍する
パターン⑥割合を表す
例：\(x\)の5%→\(\frac{5}{100}x\)
パターン⑦速さ・時間・道のりを求める
「み・は・じ」に当て嵌めて考える。
※単位が揃っているか注意！（時間と分、kmとmなど）

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。