比例と反比例「変域」をわかりやすく解説(テスト対策ポイント)
このページでは中学数学の「比例と反比例」に登場する「変域」について、子供にもわかりやすい言葉で丁寧に解説しています
- 変数「ボクたちにも限界がある!」
「変域」とは
変数の変域は、不等号<、>、\(\le\)、\(\ge\)や数直線を使って表すことがある。
ひき続き、「太郎君のゲームができる時間」の例で考えてみよう。
太郎君の「ゲームができる時間」は、「勉強をした時間」の半分になるんだったよね。
とはいえ、この「ゲームのできる時間」って、どんな数でもありえるかな??
例えば、「0分」というのはありえる??
「勉強した時間」が「0分」だったら、ありえるよね。
じゃあ、「13時間」はどうだろう。
それじゃあ、「勉強した時間」が26時間だったことになってしまうから、1日の24時間を超えちゃう※よ。
ありえないよね。
※勉強した時間とゲームをする時間は、合わせて「1日以内」として考えるよ。
じゃあ、「マイナス2時間」は??
それじゃあ「勉強した時間」が「マイナス4時間」ということになるよね。それもありえないね。
このように、「ある数」がいろいろな値をとるとはいっても、「それはありえない」という値もあることがある んだ。
なので、「ある数」とはいっても、「ココからココまで」というふうに、ありえる範囲が決まっているときに、その範囲を「変域」と呼ぶんだよ。
「変わる数の域」ということだね。
「域」とは、「限られた広さの場所」という意味で、範囲のことを表すんだよ。
変域の表し方
変数の変域は、不等号<、>、\(\le\)、\(\ge\)や数直線を使って表すことがある。
変域は「ある数が、ありえる範囲」のことだったね。
この範囲を人に伝えるとき、太郎君ならどうやって伝える?
例えば「太郎君のゲームができる時間」は、「勉強をした時間の半分」の時、ゲームをする時間の範囲はどんなだろう?
いくつかパターンを考えてみたよ。
| 勉強した時間 | マイナス20分 | 0分 | 30分 | 16時間 (960分) |
17時間 (1020分) |
| ゲームできる時間 | マイナス10分 | 0分 | 15分 | 8時間 (480分) |
8.5時間 (510分) |
| ありえるか どうか |
ありえない | ありえる | ありえる | ありえる | ありえない |
その中で「ありえるパターン」を、ピンクで色付けしたよ。
まず、勉強した時間がマイナスになるということはありえないよね。
でも、勉強した時間が0分ということはありえるね。
(ゲームできる時間は、0÷2=0で、おなじ0分になるよ。)
16時間勉強するなんて、とても大変そうだけど、ありえないことではないよね。
そして16÷2=8で、8時間ゲームが出来るようになって、
勉強した時間とゲームをする時間を合わせてちょうど24時間なので、1日以内で済むね。
では17時間勉強した場合はどうかというと、
17時間勉強することはありえないことではないけど、そうするとゲームできる時間は8.5時間になって、勉強した時間とゲームをする時間を合わせると25.5時間。
一日を超えちゃうね。
だから、これはありえないんだ。
ということは、
勉強した時間がありえる範囲は、
0分から16時間(960分)だね。
そしてゲームが出来る時間がありえる範囲は、
0分から8時間(480分)ということか。
でも、いちいちこんなふうに表を作っていたら大変だよね。そこで、「ありえる範囲」を説明する時に便利な方法が2つあるんだよ。
①不等号を使って表す
不等号を使うと、「〇〇より大きいとか、△△以上」ということを表現できるよね。
x<6
は、「xは6よりも小さい」という意味になるよね。
2<x
なら、「xは2よりも大きい」という意味。
この不等号を使って変域を表すことができるんだ。
例えば、さっきの「勉強した時間とゲームできる時間」の関係で、「勉強した時間」をxとしたとするよ。
勉強した時間がありえる範囲は「0分以上、16時間(960分)以内」だったね。
これを
0\(\le\)\(x\)\(\le\)960
と表すんだ。
※単位は「分」にそろえているよ!
「xは、0以上、960以内」という意味だね。
「x(勉強した時間)は、0(分)以上で、960(分)以内の値しかありえないよ」
と伝えられるということ。
不等号を使えば、変数が「ありえる範囲」のことをヒトコトでハッキリと伝えることができる よね。
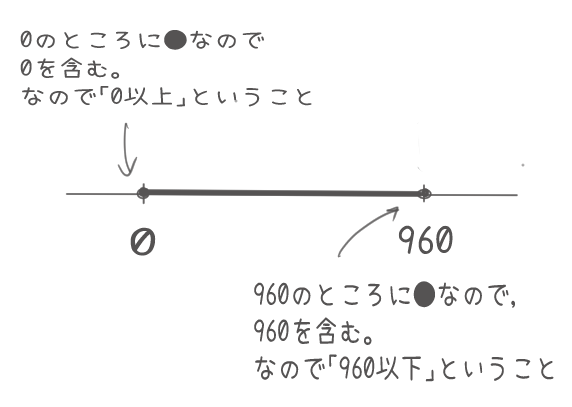
②数直線を使って表す
数直線で表すときは、「ありえる範囲」の部分に線を引く んだ。
このとき、「●」は「その数字も含む」けど、「○」は、「その数字は含まない」ことだけ注意しよう。
「xは0以上、960以内」を表す時は、このように数直線に線を引くよ。
こういう問題が出る!
変数xのとる値が次のとき、xの変域を不等号を使って表せ。
①0以上9以下
②ー3以上9未満
考え方のポイントは、「xはそれぞれ数字に対して、どの位置にいるのか」を意識すること。
①の解き方
ポイントをふまえて考えてみよう。
xは、0と9に対して、どの位置にいるかな?
「0以上」ということは、「0と同じか、それよりも大きい」ということだね。
「9以下」ということは、「9と同じか、それよりも小さい」ということだよね。
つまり、xは「0と9の間」にいることがわかるね。
xは0と9の間にいるんだから、まず書く順番は
0、 x、 9
という順番になるんだ。
あとは、それぞれの間に不等号を書き入れればいいね。
xは0に対して「以上」なんだから、
使う記号は「以上」を表す\(\le\)だね。
xは9に対して「以下」なんだから、
「以下」を表す\(\ge\)を入れればいいね。
ちょっとまって。
ここが注意ポイント。
実際、それで完成させてみると・・
0\(\le\)x\(\ge\)9
あれ?
これだと、xは「0以上」で、「9以上」という意味になっちゃうね。
そう。xと9の間に入れる記号は、「xの方が9よりも小さい」のだから、不等号の記号はx側の方が閉じていて、9側が大きく開いているものを使わなくてはいけないよ。
言葉だけで記号を選らぶのではなくて、「それぞれの数字とxの関係」をきちんと表せているかどうかチェックしながら記号を選ぶように注意してね。
答え:0\(\le\)x\(\le\)9
②の解き方
同じくxが−3と9に対してどの位置にいるか考えると・・
「ー3以上」なんだから、「−3と同じか、それよりも大きい」。
「9未満」なんだから、「9よりも小さい」。
やっぱりxは−3と0の間にいるね。
あとはそれぞれの間に「以上」と「未満」を表す記号を入れるよ。
答え:−3\(\le\)x<9
中学数学ではココを押さえればOK!
変域まとめ
- 変数のとりうる値の範囲を、その変数の変域という。
- 変域は不等号を使って表すことができる。
- 変域は数直線を使って表すことができる。
- 0<xは、「xは0よりも大きい」ことを表す(0は含まない)
- 0\(\le\)xは、「xは0以上」を表す(0も含む)
- x<0は、「xは0よりも小さい・0未満」を表す(0は含まない)
- x\(\le\)0は、「xは0以下」を表す(0を含む)
- 数直線での●は、その数字を含むことを表す
- 数直線での○は、その数字を含まないことを表す
次は「比例の式」について解説するよ!
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。









