回転体と母線とは？回転体のしくみと問題例をわかりやすく解説
中学１年生の数学で学習する「回転体」と「母線」について、回転体とはどのようにしてできているのか、母線とはどういうものかを分かりやすく解説しているよ。
回転体のテストで出る問題を例に、回転体のポイントを紹介するよ。
目次
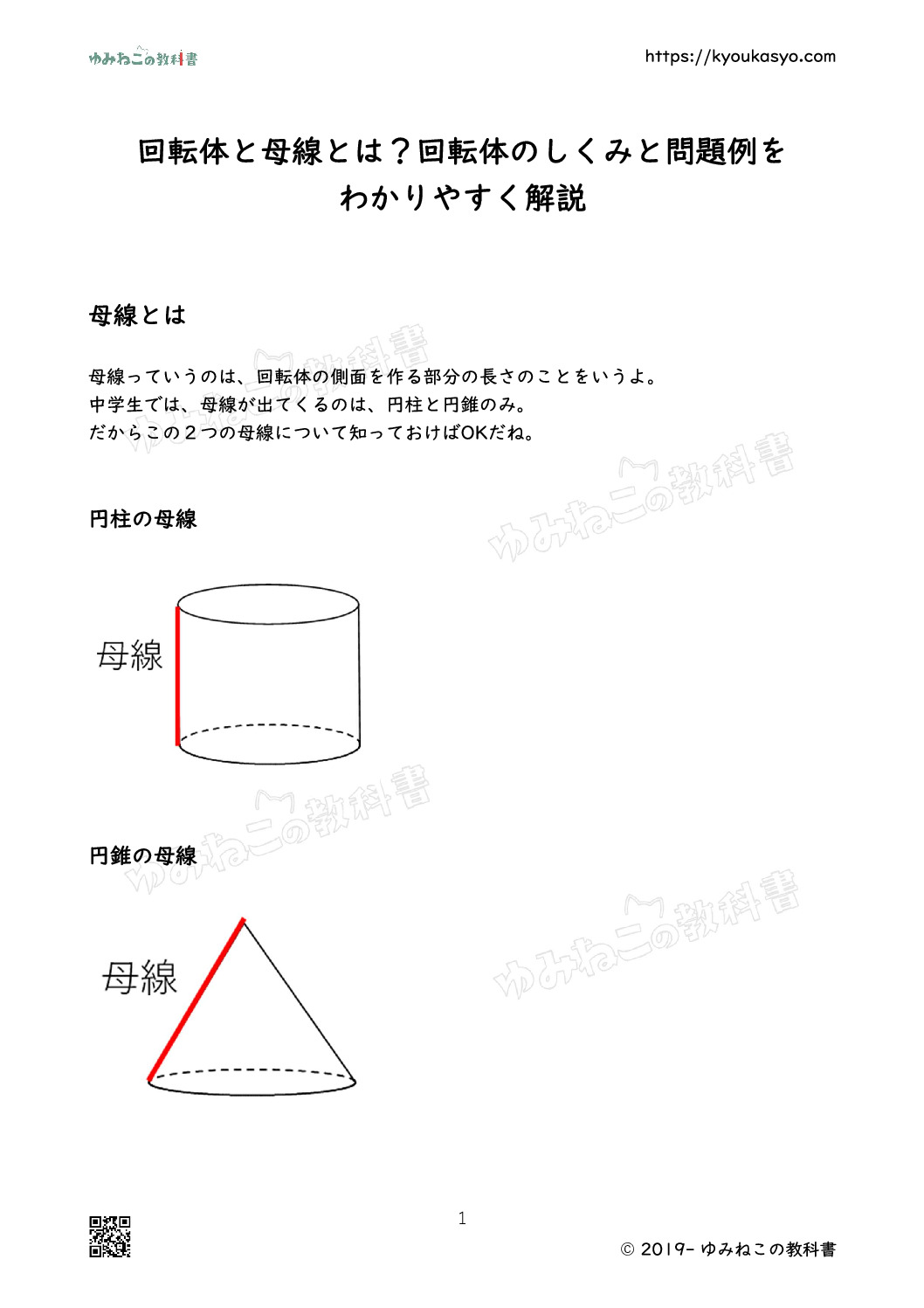
母線とは
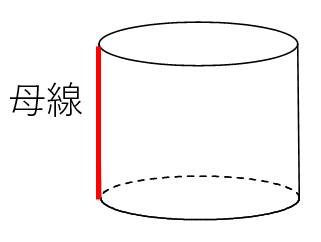
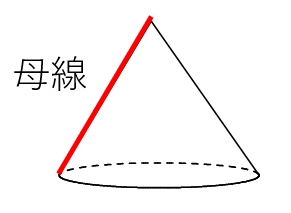
母線っていうのは、回転体の側面を作る部分の長さのことをいうよ。
中学生では、母線が出てくるのは、円柱と円錐のみ。
だからこの２つの母線について知っておけばOKだね。
円柱の母線
円錐の母線
ところで、どうして「母線」なんて名前なんだろう？
そう、「母線」は、その回転体の「お母さん」という意味で「母」という漢字が使われているんだ。
「母線」によって、その回転体が生み出されているんだよ。
「回転体を生み出す」って、どういうことだろう？と思うよね。
このあとの説明を読んだら、きっと納得すると思うよ。
回転体とは
下のような茶碗づくりやコップづくりをやったことないかな？下の台がくるくる回転するのが特徴で、台のことを「ろくろ」っていったりすんだけど・・・。
「ろくろ」と回転体はすごく似ているところがあるんだ。
実際に回転体とは何かを紹介するね。
回転体っていうのは、1つの直線を軸として平面図形を回転させてできる立体のこと。
回転体の例はこんな立体だよ。
３つともどんな特徴があるかわかるかな。とりあえず、真ん中に軸をさしてみよう。
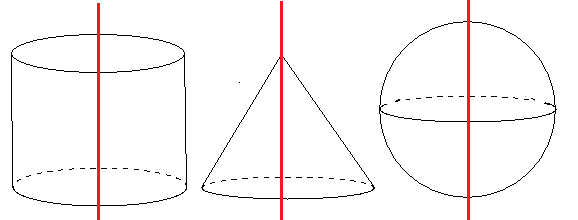
３つとも、ある平面図形を軸を中心に回転させるとできる立体ということがわかるかな？
回転体① 円柱
まず、円柱について考えようか。
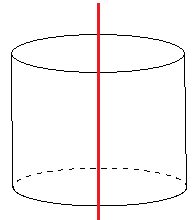
円柱って下の平面図形を軸を中心に回転させたらできるよね。
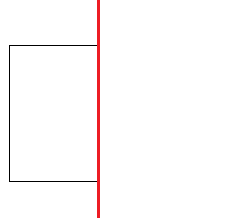
イメージしにくい人は下を見てみよう。
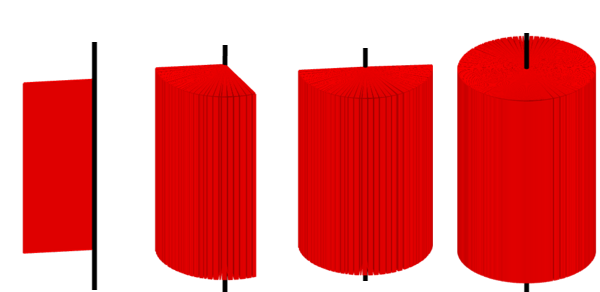
回転体② 円錐
次に、円錐について見ていこう。
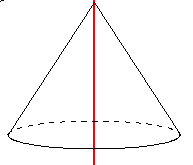
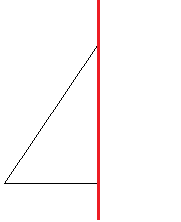
円錐って下の平面図形を軸を中心に回転させたらできるよね。
イメージしにくい人は下を見てみよう。
回転体③ 球
最後に、球について見ていこう。
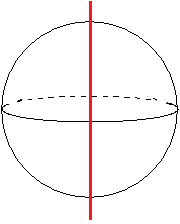
球って下の平面図形を回転させたものだよね。
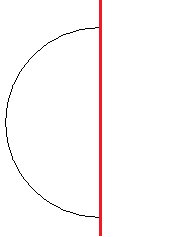
イメージしにくい人は下を見てみよう。
ここまで確認してきて、さっきの「母線」のことを思い返してみて。
円柱も円錐も、軸を中心に、母線が回転することでその回転体が生まれるのがわかるかな？
母線以外の辺が軸を中心に回転しても、回転体のような形にはならないよね。
「母線」ってどこだっけ？とテストでわからなくなってしまったら、「回転体を生み出す線」ということを考えれば、どこの線のことか思い出せるね。
回転体の見取り図を書く問題
次の平面図形を軸を中心に回転させた立体の見取り図を描きなさい。
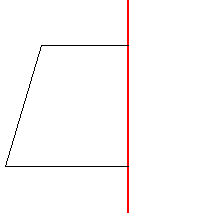
回転体の見取り図を書くポイントを紹介するね。ポイントは１点ずつ回転させることだよ。
点を軸のまわりに回転させると、円ができるよね。
例えば、台形の左上の点を回転させるとこんな感じになるよね。
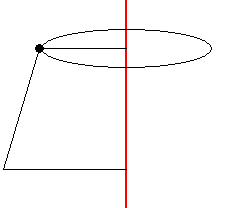
次に台形の左下の点を回転させるとこんな感じになるよね。
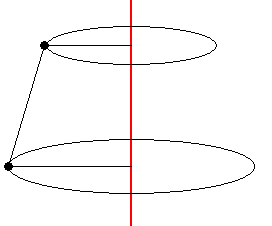
そうすると、立体の見取り図の完成だね。プリンのような立体になることがわかるよね。
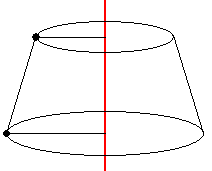
回転前の平面図形を書く問題
さっきの問題では、平面図形から回転体を書いたけど、今回は回転体から平面図形を書いてみよう。
図の回転体はどんな平面図形を回転させたものか。（円柱から、小さい円柱がくりぬかれている）
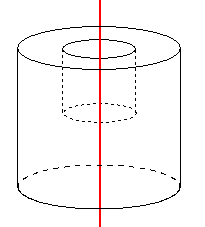
回転させる前の平面図形を想像しにくい人は、真横に真ん中で二つに切った切り口を考えるといいよ。
答えはこんな感じ。
運営者情報
ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。
とてもわかりやすいです