「累積度数・ヒストグラム・相対度数」とは?データの見方を解説
中学1年生の数学で学習する「データの見方」について、累積度数とはなにか、ヒストグラムや相対度数とは何かをくわしく紹介するよ。
累積度数とは
累積度数とは何かを説明する前に、「度数」について確認しよう。
度数とは
まず、次のデータを見てみよう。
次の値は25人の身体測定の結果(cm)
161 158 147 171 150 149 172 168
154 163 172 172 156 152 168 162
152 160 163 168 172 173 159 154
174
この25人の身体測定の結果を見ても、コメントに困るよね。だって、わかりづらいものね。
それをわかりやすく表(度数分布表)にまとめてみよう。
| 階級 以上 未満 | 度数(人) |
| 145 150 | 2 |
| 150 155 | 5 |
| 155 160 | 3 |
| 160 165 | 5 |
| 165 170 | 3 |
| 170 175 | 7 |
| 合計 | 25 |
上の表のようにまとめると、何cmの人がだいたい何人いるかわかりやすいよね。表をもとに言葉の確認をしよう。
「階級」っていうのは、データを整理するための区間のこと。
「度数」っていうのは、階級に含まれているデータの個数のこと。
「度数分布表」っていうのは、上のような表のこと。
累積度数とは
「度数」についてわかったところで、「累積度数」について説明するね。「累積度数」っていうのは、最初の階級からその階級までの度数を合計したもののこと。
さっきの度数分布表で考えると次のようになるよ。
| 階級 以上 未満 | 度数(人) | 累積度数(人) |
| 145 150 | 2 | 2 |
| 150 155 | 5 | 2+5=7 |
| 155 160 | 3 | 7+3=10 |
| 160 165 | 5 | 10+5=15 |
| 165 170 | 3 | 15+3=18 |
| 170 175 | 7 | 18+7=25 |
| 合計 | 25 |
累積度数を見れば、その階級までの度数(人数)がわかるよ。
例えば、160cm未満の人はすぐに10人とわかるよね。
| 階級 以上 未満 | 度数(人) | 累積度数(人) |
| 145 150 | 2 | 2 |
| 150 155 | 5 | 2+5=7 |
| 155 160 | 3 | 7+3=10 |
ヒストグラムとは
ヒストグラムっていうのは、度数分布表をわかりやすく縦棒のグラフに表したものだと思えばOK。
さっきの度数分布表をヒストグラムにしてみるとこんな感じになるよ。
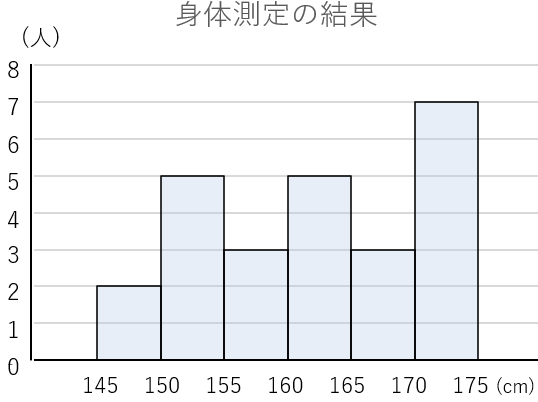
ヒストグラムにすると、どのくらいの身長の人が何人いるかがわかりやすいね。ちなみにヒストグラムのことを「柱状グラフ」とも言ったりするよ。
度数折れ線とは
度数折れ線っていうのは、ヒストグラム(柱状グラフ)の長方形の上の中点を結んだ折れ線グラフのことだよ。
さっきのヒストグラムで度数折れ線を書くと次のようになるよ。
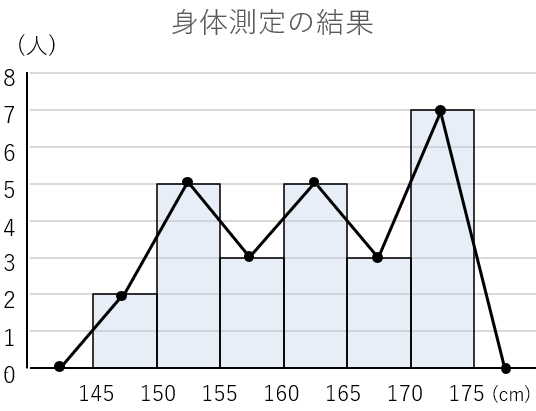
気をつけなくてはいけないことは、左端の階級の左(145未満)を0にすることと、右端の階級の右(175以上)を0にすることだよ。
ちなみに度数折れ線のことを「度数分布多角形」とも言ったりするよ。
相対度数とは
相対度数とは、各階級の度数を合計の度数で割った値のこと。次の式で表すことができるよ。
相対度数の求め方
相対度数=\(\frac{その階級の度数}{度数の合計}\)
さっきの度数分布表で相対度数を求めてみよう
| 階級 以上 未満 | 度数(人) | 相対度数 |
| 145 150 | 2 | 2÷25=0.08 |
| 150 155 | 5 | 5÷25=0.20 |
| 155 160 | 3 | 3÷25=0.12 |
| 160 165 | 5 | 5÷25=0.20 |
| 165 170 | 3 | 3÷25=0.12 |
| 170 175 | 7 | 7÷25=0.28 |
| 合計 | 25 | 1.00 |
相対度数の意味
度数分布表で、145以上150未満の階級の相対度数は0.08だったよね。
どういう意味かっていうと全体の8%の人が145cm以上150cm未満の身長ということだよ。
つまり、相対度数っていうのは%みたいな割合だと考えればOK。
割合だから、すべての割合を合計したら100%になるよね。だから、すべての相対度数の合計は1.00になるよ。
相対度数を求める必要性
次の2つの度数分布表はA中学校とB中学校の身長を表したものなんだけど、どっちの方が身長が高い人が多いと言えるかな?
| A中学校 | B中学校 | |
| 階級 以上 未満 | 度数(人) | 度数(人) |
| 145 150 | 2 | 1 |
| 150 155 | 5 | 15 |
| 155 160 | 3 | 8 |
| 160 165 | 5 | 6 |
| 165 170 | 3 | 7 |
| 170 175 | 7 | 13 |
| 合計 | 25 | 50 |
170cm以上175cm未満の数を見ると、A中学校7人、B中学校13人でB中学校の方が身長が高いのかなと思ってしまうんだけど、合計の人数を見なくちゃいけないんだ。
A中学校とB中学校では合計の人数が違うから、度数だけで比較しちゃだめだよ。そこで使うのが相対度数。
実際に2つの中学校の相対度数を求めてみたよ。
| A中学校 | A中学校 | B中学校 | B中学校 | |
| 階級 以上 未満 | 度数(人) | 相対度数 | 度数(人) | 相対度数 |
| 145 150 | 2 | 0.08 | 1 | 0.02 |
| 150 155 | 5 | 0.20 | 15 | 0.30 |
| 155 160 | 3 | 0.12 | 8 | 0.16 |
| 160 165 | 5 | 0.20 | 6 | 0.12 |
| 165 170 | 3 | 0.12 | 7 | 0.14 |
| 170 175 | 7 | 0.28 | 13 | 0.26 |
| 合計 | 25 | 1.00 | 50 | 1.00 |
相対度数を考えると170cm以上175cm未満の人の割合はA中学校の方が多いことがわかるね。
ここまで学習した相対度数のポイントを下にまとめるね。
相対度数のポイント
・相対度数=\(\frac{その階級の度数}{度数の合計}\)で求められる
・その階級の割合のこと
・すべて合計したら1.00になる
・全体のデータの個数が違うときに比較することができる
相対度数の問題
相対度数の問題はよくテストに出るから、しっかり求められるようにしよう。
下の表は、40人の握力を度数分布表にまとめたもので35 kg 以上40kg 未満の階級の相対度数を求めなさい。
| 階級(kg) 以上 未満 | 度数(人) |
| 25 30 | 4 |
| 30 35 | 5 |
| 35 40 | 7 |
| 40 45 | 4 |
| 45 50 | 5 |
| 合計 | 25 |
35以上40未満の度数(人数)は7人で、合計人数が25人なので相対度数は次の式で求められるよ。
相対度数=\(\frac{その階級の度数}{度数の合計}\)
=\(\frac{7}{25}\)
=0.28
35以上40未満の相対度数は0.28が答えだよ。
つまり28%の人が35以上40未満ということだね。
累積相対度数とは
相対度数についてわかったところで、「累積相対度数」について紹介するね。さっきの「累積度数」と似ているからイメージしやすいと思うよ。
「累積相対度数」とは、最初の階級からその階級までの相対度数を足したもののこと。
| 階級 以上 未満 | 度数(人) | 相対度数 | 累積相対度数 |
| 145 150 | 2 | 2÷25=0.08 | 0.08 |
| 150 155 | 5 | 5÷25=0.20 | 0.08+0.20=0.28 |
| 155 160 | 3 | 3÷25=0.12 | 0.28+0.12=0.40 |
| 160 165 | 5 | 5÷25=0.20 | 0.40+0.20=0.60 |
| 165 170 | 3 | 3÷25=0.12 | 0.60+0.12=0.72 |
| 170 175 | 7 | 7÷25=0.28 | 0.72+0.28=1.00 |
| 合計 | 25 | 1.00 |
例えば、155cm以上160cm未満の累積相対度数は0.40になっているよね。つまり、40%の人が160cm未満であることがわかるね。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。



めちゃくちゃわかりやすかったです(´;ω;`) 受験生なのでとても助かりました、本当にありがとうございました!