比例・反比例とは？「ｙはｘに比例・反比例する」比例定数の求め方
目次
比例とは
小学校でも比例については勉強したね。
比例っていうのは、
「一方が２倍３倍になると、もう一方も２倍・３倍になる関係のこと」だったよね。
イメージしやすいように、身の回りの比例の例を２つ紹介するね。
身の回りの比例の例①
「リンゴを買う個数」と「リンゴの値段」
八百屋さんで、リンゴを買う時を考えてみよう。
買うリンゴの個数が１個なら、１個分の値段。
リンゴが２個（１個の２倍）なら、値段も２個分（１個分の２倍）になるね。
一方が２倍・３倍になると、もう一方も２倍・３倍になっているね。
だから「リンゴを買う個数と、リンゴの値段」は比例の関係だね。
実際に金額を計算してみよう。
リンゴがもし１個１００円だったら、２個で２００円、３個で３００円。
「リンゴを買う個数が２倍・３倍」になったら、ちゃんと「リンゴの値段も２倍・３倍」になっているね。
表でも確認してみよう。
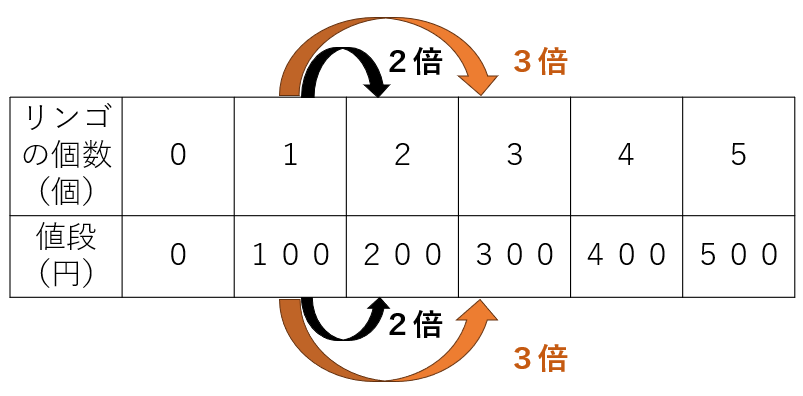
表にすると、さらに比例の関係であることがよくわかるね。
さて、小学校で習った比例だけれど、どうしてまた中学校でも学習するのかというと、
この「比例の関係」を、中学の数学では「文字」を使って考えるんだ。
中学数学では、「文字を使った式」が使えるようになっているからね。
では、この「リンゴを買った個数」と「リンゴの値段」の関係を、文字を使って表してみよう。
「リンゴのを買った個数」をｘ、
「リンゴの値段」をｙとするよ。
すると、下のような表ができるね。
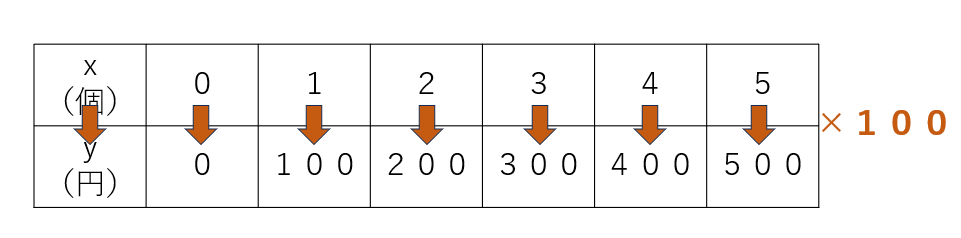
この表をみると、ｘとｙの関係ってどうなっているかな。
たろう上の段（ｘ）を１００倍すると、下の段（ｙ）になっているね。
そうだね。なので、ｘとｙの関係は、ｙ＝１００ｘと表すことができるんだ。
この式の形をよく覚えておいてね。
では、次の例も見てみよう。
身の回りの比例の例②
「水を入れている時間」と「水の深さ」
水道の蛇口をひねった時、１分で２ｃｍずつ水が入るとするよ。
２分経ったら水の深さは４ｃｍ、３分経ったら、水の深さは６ｃｍだよね。
「水を入れている時間」が２倍・３倍になると、「水の深さ」も２倍・３倍になることがわかるかな。
これも、表で確認しよう。
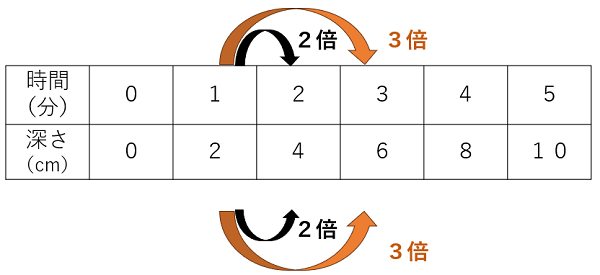
表で確認してみても、比例の関係であることがよくわかるね。
それでは、中学生らしく「文字」を使って考えてみよう。
「水を入れる時間」をｘ、
「水の深さ」をｙとするよ。
すると、下のような表ができるね。
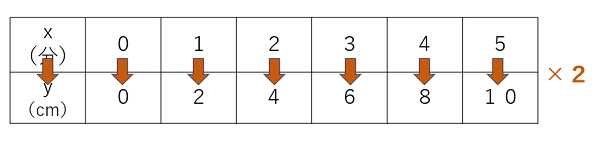
今度は、上の段（ｘ）を２倍すると、下の段（ｙ）になっているね。
なので、ｘとｙの関係は、ｙ＝２ｘと表せる。
さっきのリンゴのケースでは、「ｙ＝100ｘ」で表せたね。
そして、今度は「ｙ＝２ｘ」。
なんだか形が似ていることに気が付いたかな？
比例の式の形「ｙ＝ａｘ」
さっきの「ｙ＝１００ｘ」とか「ｙ＝２ｘ」は、比例の式の形なんだよ。
ｘの前の「１００」とか、「２」は、そのときどきで数字が変わるよね。
なので、この「そのときどきで変わる数字」をひとまず「ａ」であらわしちゃうんだ。
そうすると、
比例の式の形は「ｙ＝ａｘ」と表すことができるよ。
くまごろうこのａの部分に、そのときどきでいろんな数字が入るんだね。
では実際に問題に挑戦してみよう。
（問）次の中で、ｙがｘに比例しているものを選びなさい。
ア：ｙ＝２ｘ
イ：ｙ＝\(\frac{３}{ｘ}\)
ウ：ｙ＝２ｘ＋３
エ：ｙ＝２ｘ２
答えは「ア」。
「ア」だけがｙ＝ａｘの形になっているので正解になるよ。
余裕があったら読んでみよう！
（おまけ： 2年生で学習すること）
さっきの水の入れる時間と深さの問題を例に考えよう。
水を入れている時間が「０分」のとき、水の深さは「０ｃｍ」なのはわかるよね。だって、０分のときは、まだ容器の中に水が入っていないんだから当たり前だよね。
１年生の数学では、「容器が空っぽの状態」からスタートする式しか学習しないけれど、２年生になると、「容器の中に、あらかじめ水が入っている状態」からスタートする式を学習したりするよ。
たとえば、「すでに深さ10㎝の水が入っている容器」に、１分間に２㎝ずつ水を入れた場合、「水を入れている時間」と「水の深さ」はどんな式になるだろう。
答えは、ｙ＝２ｘ＋１０。
さっきの式に、「１０㎝」の「１０」が足されるんだね。
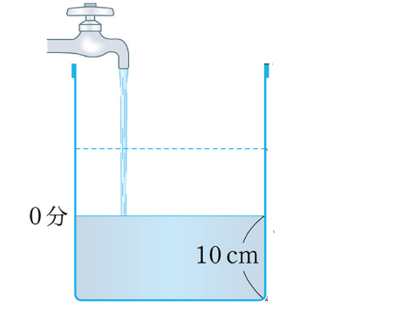
どうしてこんな話をしたかというと、この「ｙ＝２ｘ＋１０」は、「一次関数」の式なんだ。
比例の式は「ｙ＝２ｘ」だよね。
とっても似ているよね。
だから、「比例と一次関数の違いって？」と混乱してしまうことがよくあるんだ。
比例は、実は「一次関数」の仲間だよ。ただ、一次関数の「＋１０」のように、余計な？部分が無いものが「比例」なんだ。
２年生の数学でもくわしく学習することになるけれど、せっかくだからちょっと覚えておいてね。
比例定数とは
教科書一定の数やそれを表す文字を定数と言い、比例の式の中の文字aは定数であり「比例定数」と呼ぶ。
「比例定数」なんて、かしこまった言葉で言われると、なんだか難しそうに聞こえるけれど、実はすごく簡単なことを言っているだけなんだ。
ここまで学習してきたように、比例は必ずｙ＝ａｘの形で表されるんだったよね。この「ａ」の部分だけが式によって変わるんだから、この「ａ」の部分ってとても需要だよね。（だって、のこりのｙとｘは変わらないからね）
この「ａ」のことを「比例定数」っていうんだ。
比例の式の重要な「ａ」に分かりやすいように名前をつけてあげただけだね。
なぜ「比例定数」という名前なのかというと、「リンゴの例え」では、リンゴを何個買ってもかならずｙはｘの「１００倍」だったよね。
「水の例え」でも、水を何分入れようが、何時間入れようが、かならずｙはｘの「２倍」だったよね。
２つの例とも、「リンゴを買った数」」とか、「最終的なリンゴの値段」とか、「水を入れた時間」とか、「水の深さ」って、そのときどきで変わるよね。
でも、この「１００」という数字と「２」という数字はずっと「一定」のまま。
そう、「一定のままの数字」だから「定数」なんだ。
そして、「比例の式の中で、ずっと一定のままの数」だから、「比例定数」だよ。
では、問題でも確認してみよう。
（問）次の比例の式の比例定数をそれぞれ答えなさい。
ア：ｙ＝２ｘ
イ：ｙ＝－３ｘ
ウ：ｙ＝ｘ
エ：ｙ＝\(\frac{１}{３}\)ｘ
答えを確認しよう。
比例定数はｙ＝ａｘの「ａ」だよね。
ｘの前の係数が「ａ」にあたるから、それをそのまま答えればＯＫ。
ア：２
イ：－３
ウ：１（ｘの前には「１」が省略されている）
エ：\(\frac{１}{３}\)
比例定数の求め方
教科書ｙがｘに比例するとき、ｙ÷ｘで比例定数が求まる
比例定数の求め方には「ｙ÷ｘ」を計算すればいいということだね。
でも、なぜそうなるかを考えてみよう。
さっきの「水の例」の表をもう一度見てみよう。
「ｘ」を２倍したら「ｙ」になっているね。つまり「ｙ＝２ｘ」と表すことができて、この「２」が比例定数だったんだよね。
この「２」という数字は、「ｙ」を「ｘ」で割れば出てくることは分かるかな？
①ｘ＝１、ｙ＝２のところに注目しよう。
ｙ÷ｘ
＝２÷１
＝２
②ｘ＝２、ｙ＝４のところに注目しよう
ｙ÷ｘ
＝４÷２
＝２
くまごろう①のときも②のときも比例定数はｙ÷ｘで求められているね。
「ｘ」に、ある数をかけた結果が「ｙ」なんだから、「ある数」を求めたいのであれば、「ｙ」を「ｘ」で割ればいいよね。
だから、ｙ÷ｘで「ある数＝比例定数」が求まるんだね。
では問題に挑戦してみよう。
（問）ｙはｘに比例しており、ｘ＝３のとき、ｙ＝９になる。
比例定数を求めよ。
比例の比例定数はｙ÷ｘで求まるから、
比例定数ａ＝９÷３＝３になるね。
「比例定数」なんて難しい言葉に感じるけれど、実際に学習してみるとそんなに難しいことではないね。
だけれどここから先、１年生では「反比例」、２年生は「１次関数」、３年生では「二乗に比例する関数」というのをやるので、ごっちゃになっちゃう人が多いんだ。
なので、ここでしっかりと押さえておこうね。
反比例とは
反比例も小学校で勉強したと思うよ。
反比例というのは、「一方が２倍・３倍になると、もう一方は\(\frac{１}{２}\)倍・\(\frac{１}{３}\)倍になる関係のこと」だったよね。
身の回りの反比例の例を紹介するね。
身の回りの反比例の例
「分ける人数」と「１人分の個数」
みかんが６個あったとするよ。１人で分けたら、１人分の個数は６個になるよね。いわゆる独り占めってやつだね。
２人で分けたら、１人分の個数は３個
３人で分けたら、１人分の個数は２個
６人で分けたら、１人分の個数は１個
表にまとめてみよう。４人と５人の時は切りよく分けられないので、空欄にしたよ。
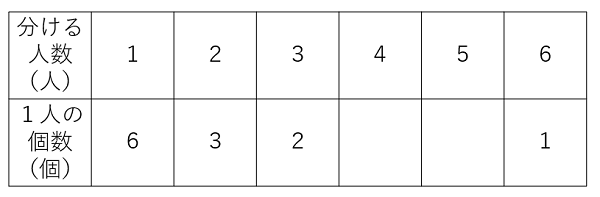
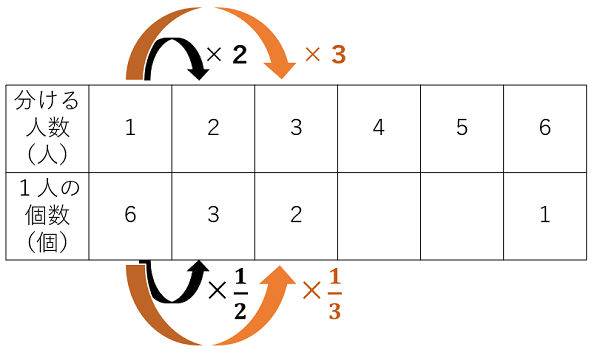
「分ける人数」と「1人分の個数」は反比例の関係であることがよくわかるね。
では、中学生らしく「文字」を使って考えてみよう。
「分ける人数」をｘ、「１人分の個数」をｙとすると次のような表ができるよ。
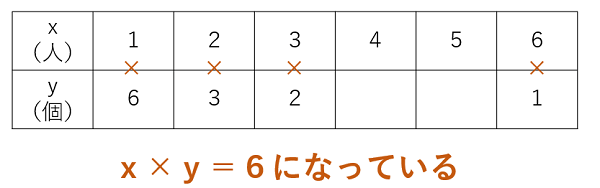
たろう今度は、上の段（ｘ）と下の段（ｙ）をかけたら「６」になっているね。
ｘ×ｙ＝６を、移項を使って「ｙを求めるための式」に変えてみよう。
ｙ＝６÷ｘ
もう少し整理して
ｙ＝\(\frac{６}{ｘ}\)
という式になるよ。
比例の式の形「ｙ＝\(\frac{ａ}{ｘ}\)」
さっきのｙ＝\(\frac{６}{ｘ}\)がまさに反比例の式の形なんだ。
反比例の式の形はｙ＝\(\frac{ａ}{ｘ}\)と表されるよ。
比例の式と同じで、この「ａ」にはその式によって色々な数字が入るよ。
実際に問題に挑戦してみよう。
（問）次の中で、ｙがｘに反比例しているものを選びなさい。
ア：ｙ＝２ｘ
イ：ｙ＝\(\frac{３}{ｘ}\)
ウ：ｙ＝２ｘ＋３
エ：ｙ＝２ｘ２
答えは「イ」。
「イ」だけがｙ＝\(\frac{ａ}{ｘ}\)の形になっているので反比例の式になっているよ。
反比例の比例定数
これがちょっと紛らわしいところなんだけど、
反比例でも「比例定数」っていうんだ。反比例の比例定数は、反比例の式ｙ＝\(\frac{ａ}{ｘ}\)の「ａ」のことをいうよ。
余裕があったら読んでみよう！
どうして反比例なのに「比例定数」っていうの？
ｙ＝\(\frac{ａ}{ｘ}\)の式を、よーく見てみよう。
これって、実はｙ＝a×\(\frac{１}{ｘ}\)と書くこともできるよね。
これって、比例の式「ｙ＝ａｘ」が「ｙはｘに比例している」と言うのに対して、「ｙ＝a×\(\frac{１}{ｘ}\)」は「ｙは\(\frac{１}{ｘ}\)に比例している」と言うことができるという事なんだ。
たとえるなら、
「私は、ピーマンの入った料理が好き」＝「ピーマンが好き」
という状態が「比例」だったとしたら、
「私は、ピーマンの入った料理が嫌い」＝「ピーマンが嫌い」
という状態が「反比例」だとするよ。
でも反比例の「ピーマンが嫌い」という状態を説明するのに、
「私は、ピーマンの入っていない料理が好き」＝「ピーマンが嫌い」
と言い換えることができるよね。
この感覚とおなじ。
「ｙはｘに比例している」の反対である「ｙはｘに反比例している」は、「ｙは\(\frac{１}{ｘ}\)に比例している」と言い換えることができるということ。
なので、反比例の状態も「比例」のひとつと考えて、aのことを「比例定数」と呼ぶ、と考えることができるよ。
では、実際に問題を解いてみよう。
（問）反比例の式で比例定数をそれぞれ答えなさい。
ア：ｙ＝\(\frac{２}{ｘ}\)
イ：ｙ＝－\(\frac{３}{ｘ}\)
ウ：ｙ＝\(\frac{１}{ｘ}\)
答えを確認しよう。
反比例の比例定数はｙ＝\(\frac{ａ}{ｘ}\)の「ａ」だから分子にある数を見たらいいよ。
ア：２
イ：－３
ウ：１
反比例の比例定数の求め方
教科書ｙがｘに反比例するとき、ｘ×ｙで反比例の比例定数が求まる
反比例の比例定数の求め方はｘ×ｙで計算すればいいんだけど、なんでそうなるかを考えてみよう。
「みかんを分ける例」の表を確認すると、ｘとｙをかけたら比例定数である「６」になっているのがわかるね。
このように、ｘとｙで反比例の比例定数が求まるよ。
では、問題を解いてみよう。
（問）ｙはｘに反比例するとき、ｘ＝３のとき、ｙ＝９になる。比例定数を求めよ。
反比例の比例定数はｘとｙをかけたものだったから、
比例定数ａ＝３×９＝２７になるね。
まとめ
比例や反比例とは、ｘとｙがどういう関係なのか。比例定数とは何で、どうやって求められるのか。
比例・反比例はごっちゃになってしまいがちだから下にまとめたよ。
比例と反比例
- 比例の式は「ｙ＝ａｘ」
比例定数「ａ」は「ｙ÷ｘ」で求めることができる - 反比例の式は「ｙ＝\(\frac{ａ}{ｘ}\)」
比例定数「ａ」は「ｘ×ｙ」で求めることができる
運営者情報
ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。
