反比例のグラフと表から式を求めよう（手順をわかりやすく解説）
中学１年生の数学で学習する「反比例の式」について、「反比例のグラフ」と「反比例の関係を表す表」から反比例の式を求める方法をわかりやすく解説するよ。
目次
表を使った反比例の式の求め方
それでは、まずは「反比例の関係を表す表」から、反比例の式を求める方法について説明していくよ。
次の表はｘとｙが反比例の関係であることを表しているよ。
だってｘが２倍、３倍になると、ｙは\(\frac{１}{２}\)倍、\(\frac{１}{３}\)倍になっているからね。
では、この反比例の表から式を求めてみよう。
反比例の式はｙ＝\(\frac{ａ}{ｘ}\)で表されるんだったよね。
ａは「比例定数」といって、数字が入るね。
ａを求めることができたら、反比例の式で表すことができるね。
ちなみに、反比例でも比例定数っていうからね。反比例定数なんてないよ。
「反比例の比例定数ってなんだっけ？」と不安になったら、反比例についての解説ページをもういちど確認しよう。
ｙ＝\(\frac{ａ}{ｘ}\)の比例定数ａを求める
反比例の式ｙ＝\(\frac{ａ}{ｘ}\)を割り算を使って表すと次のようになるよ。
ｙ＝ａ÷ｘ
今回ａを求めたいから、「ａ＝○○」という形に変えるよ。
ｙ＝ａ÷ｘ ←左辺と右辺をひっくり返すよ
ａ÷ｘ＝ｙ ←左辺のｘを消すために、両辺にｘをかけるよ
ａ＝ｙ×ｘ ←「ｙ×ｘ」は「ｘ×ｙ」と同じ
ａ＝ｘ×ｙ
この「ａ＝ｘ×ｙ」ということさえわかれば、こっちのもの。
反比例の比例定数「ａ」はｘとｙをかければ求めることができるということだよね！
これさえ分かれば、反比例の式を求める問題はマスターしたも同然だよ。
さっきの表に戻ろう。
反比例の比例定数ａは、ｘとｙをかけたら求まるんだったよね。
ｘ＝１のとき、ｙ＝４だから、ａ＝ｘ×ｙ＝１×４＝４
ｘ＝２のとき、ｙ＝２だから、ａ＝ｘ×ｙ＝２×２＝４
ｘ＝３のとき、ｙ＝\(\frac{４}{３}\)だから、ａ＝ｘ×ｙ＝３×\(\frac{４}{３}\)＝４
ｘ＝４のとき、ｙ＝１だから、ａ＝ｘ×ｙ＝４×１＝４
ｘ＝－１のとき、ｙ＝－４だから、ａ＝ｘ×ｙ＝（－１）×（－４）＝４
ｘ＝－２のとき、ｙ＝－２だから、ａ＝ｘ×ｙ＝（－２）×（－２）＝４
ｘ＝－３のとき、ｙ＝－\(\frac{４}{３}\)だから、ａ＝ｘ×ｙ＝（－３）×（－\(\frac{４}{３}\)）＝４
ｘ＝－４のとき、ｙ＝－１だから、ａ＝ｘ×ｙ＝（－４）×（－１）＝４
それぞれ計算した結果、ｘがいくつのときでも反比例の比例定数ａ＝４になっているね。
全部を計算したけれど、どこか１つだけのｘとｙで計算しても求めることができるよ。
ｙ＝\(\frac{ａ}{ｘ}\)のａに代入する
反比例の比例定数が求まったら、ｙ＝\(\frac{ａ}{ｘ}\)のａに代入しよう。さっきの問題では、比例定数はａ＝４なので次のような式になるよ。
ｙ＝\(\frac{ａ}{ｘ}\)にａ＝４を代入して
ｙ＝\(\frac{４}{ｘ}\)
これが今回求めたい反比例の式だよ。
くまごろう反比例の式がｙ＝\(\frac{ａ}{ｘ}\)になることさえ覚えていれば楽勝だね。
反比例の表から簡単に式を求める方法についてまとめたよ。
反比例の表から簡単に式を求める方法
- 表を縦に見て、ｘとｙの値をかける
- かけて求まった答えをｙ＝\(\frac{ａ}{ｘ}\)のａに代入する
反比例の表から式を求める練習
（１）下の表は反比例を表している。ｙをｘの式で表しなさい。
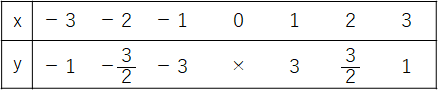
表を縦に見て、ｘとｙの値をかけたものが比例定数ａになるから、
ｘ＝１のときｙ＝３という値に注目しよう。ｘ×ｙ＝１×３＝３だから、ｙ＝\(\frac{３}{ｘ}\)という反比例の式になるよ。
（２）ｙはｘに反比例しているとき、ｘ＝５のとき、ｙ＝３である。ｙをｘの式で表しなさい。
この問題は表ではないんだけど、あえて表にすると次のようになるよ。
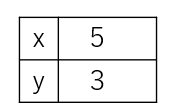
表を縦に見て、ｘとｙの値をかけたものが比例定数ａになるから、
ｘ＝５のときｙ＝３なので、ｘ×ｙ＝５×３＝１５になる。だからｙ＝\(\frac{１５}{ｘ}\)という反比例の式になるよ。
反比例の表から式を求める別の方法
さっきまではｙ＝\(\frac{ａ}{ｘ}\)をａ＝ｘ×ｙという形にして、比例定数ａを求めてきたけど、
ｙ＝\(\frac{ａ}{ｘ}\)にｘとｙをそのまま代入する方法もあるよ。
さっきの問題を例にやってみよう。
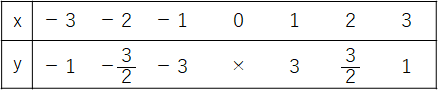
ｘ＝１のときｙ＝３という値に注目しよう。ｙ＝\(\frac{ａ}{ｘ}\)にｘ＝１、ｙ＝３を代入すると
３＝\(\frac{ａ}{１}\)
３＝ａ
となり、比例定数が３になることがわかるね。あとはいつもどおりｙ＝\(\frac{ａ}{ｘ}\)に比例定数ａ＝３を代入して、ｙ＝\(\frac{３}{ｘ}\)という式になるよ。
反比例のグラフから式を求める方法
反比例の表から式を求めることができたら、グラフから式を求めるのは楽勝だよ。違いはグラフの座標を読み取るだけ。
では実際に問題をやってみよう。
（例）次のグラフは反比例を表している。このグラフの式を求めなさい。
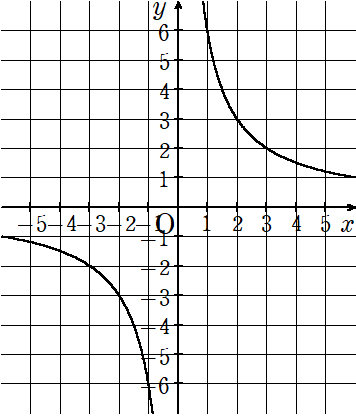
「キリのよい」座標を読み取ると（１，６）（２，３）（３，２）（６，１）（－１，－６）（－２，－３）（－３，－２）（－６，－１）の８つ。
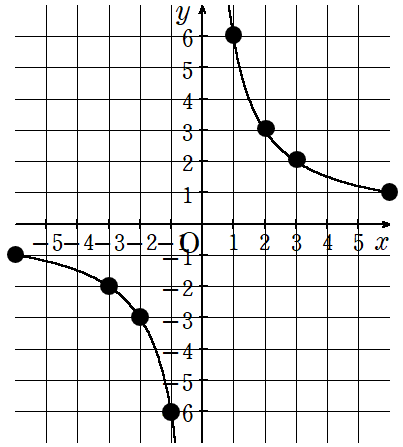
反比例の式ｙ＝\(\frac{ａ}{ｘ}\)の比例定数ａはｘとｙをかけたら求まるんだったから、８つの座標のうち、１つの座標のｘとｙをかけたらａが求まるよ。
反比例のグラフは（１，６）を通るので、比例定数は
ａ＝ｘ×ｙ＝１×６＝６
になるよ。
反比例の式ｙ＝\(\frac{ａ}{ｘ}\)にａ＝６を代入して
ｙ＝\(\frac{６}{ｘ}\)という反比例の式ができあがるね。
くまごろう座標を読み取ることができて、反比例の式がｙ＝\(\frac{ａ}{ｘ}\)になることさえ覚えていれば楽勝だね。
反比例のグラフから式を求める方法についてまとめたよ。
反比例のグラフから式を求める方法
- グラフで「キリの良い点」のｘとｙを読み取る
- ｘとｙの座標をかける
- かけて求まった答えをｙ＝\(\frac{ａ}{ｘ}\)のａに代入する
反比例のグラフから式を求める練習
（１）下のグラフは反比例を表している。ｙをｘの式で表しなさい。
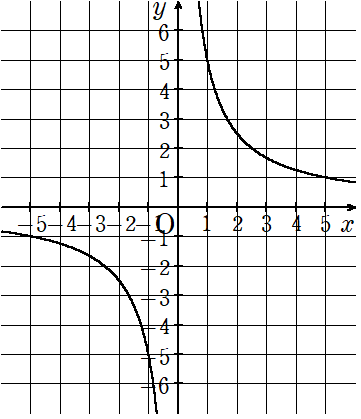
「キリのよい」座標を読み取ると（１，５）（５，１）（－１，－５）（－５，－１）の４つ。
反比例の式ｙ＝\(\frac{ａ}{ｘ}\)の比例定数ａはｘとｙをかけたら求まるんだったから、４つの座標のうち、１つの座標のｘとｙをかけて求めてみよう。
反比例のグラフは（１，５）を通るので、比例定数は
ａ＝ｘ×ｙ＝１×５＝５
になるよ。
反比例の式ｙ＝\(\frac{ａ}{ｘ}\)にａ＝５を代入して
ｙ＝\(\frac{５}{ｘ}\)という反比例の式ができあがるね。
（２）下のグラフは反比例を表している。ｙをｘの式で表しなさい。
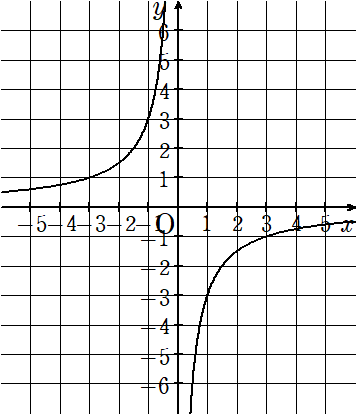
「キリのよい」座標を読み取ると（１，－３）（３，－１）（－１，３）（－３，１）の４つ。
反比例の式ｙ＝\(\frac{ａ}{ｘ}\)の比例定数ａはｘとｙをかけたら求まるんだったから、４つの座標のうち、１つの座標のｘとｙをかけて求めてみよう。
反比例のグラフは（３，－１）を通るので、比例定数は
ａ＝ｘ×ｙ＝３×（－１）＝－３
になるよ。
反比例の式ｙ＝\(\frac{ａ}{ｘ}\)にａ＝－３を代入して
ｙ＝－\(\frac{３}{ｘ}\)という反比例の式ができあがるね。
運営者情報
ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。
