「円錐の展開図」半径・弧の長さ・中心角の求め方をくわしく解説
中学1年生の数学で学習する「立体の展開図」のうち、「円錐の展開図」から、底面の円の半径や、側面になるおうぎ形の弧の長さや中心角を求める方法をイラストと例題を使ってわかりやすく解説するよ。
円錐の展開図の性質を復習しておこう。
円錐の展開図の大切な性質
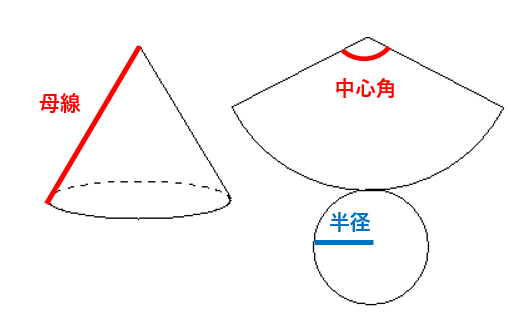
①円錐の母線は、展開図では、おうぎ形の半径になる。
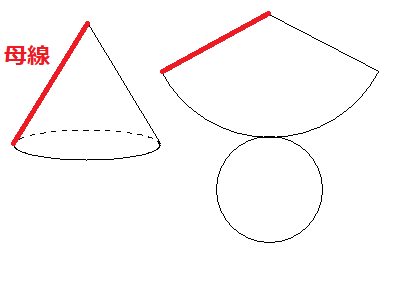
②展開図のおうぎ形の弧の長さと、底面の円周の長さは等しくなる
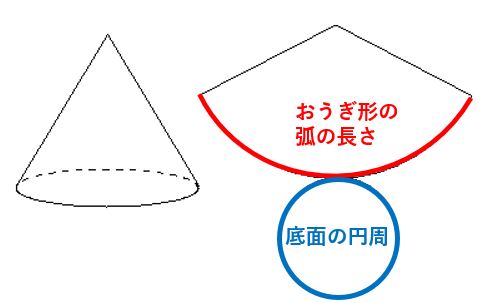
円錐の展開図と半径の求め方
まず、円錐の展開図の問題で出ることが多い「底面の半径の求め方」を解説するよ。
円錐の「母線」と「底面の半径」と「展開したときのおうぎ形の中心角」には大切な関係があるんだよ。
どんな関係があるかを例題を解きながら考えていこう。
円錐の底面の半径を求める例題
問
下のような円錐があり、展開図を右にかいた。この円錐の底面の半径を求めなさい。
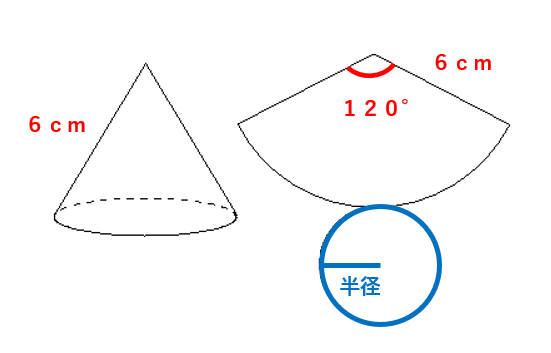
おうぎ形の弧の長さと底面の円周は等しかったよね。だから、おうぎ形の弧の長さの長さを求めたら、底面の半径が求まりそうだね。
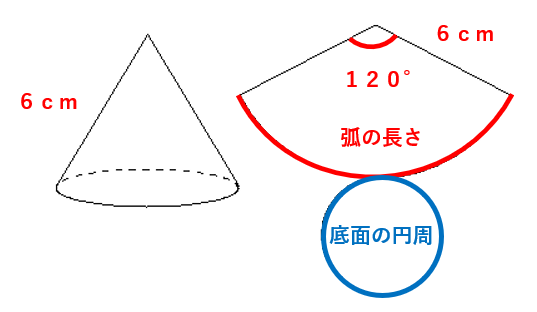
STEP1 弧の長さを求めよう。
おうぎ形の弧の長さを求める公式は次の通りだったよね。
直径×円周率×\(\frac{中心角}{360}\)
今回の問題では、おうぎ形の半径(母線)が6cm、中心角120°で円周率はπを使うから、式に当てはめると
直径×円周率×\(\frac{中心角}{360}\)
=12×π×\(\frac{120}{360}\)
=4π (cm)
おうぎ形の弧の長さと底面の円周が等しいから、底面の円周も4πcmだとわかるね。
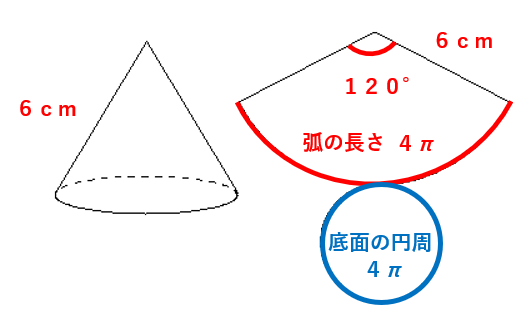
STEP2底面の円の半径を求める
底面の円周が4πだから、半径も求められそうだよね。円周の求め方は次の通りだったね。
円周=直径×円周率
この式に、円周4π、円周率πを代入すると
4π=直径×π
上の式から直径=4であることがわかるね。だから、底面の半径は4÷2=2cmということだね。
円錐の「母線と中心角」から「底面の半径」を求める方法
円錐の「母線と中心角」から「底面の半径」を求める方法
- 展開図を書いて、おうぎ形の弧の長さを求める
公式:直径×円周率×\(\frac{中心角}{360}\) - おうぎ形の弧の長さと、底面の円周は等しいことから、底面の半径を求める。
公式:円周=直径×円周率
円錐の「母線」と「展開したときのおうぎ形の中心角」がわかると、「底面の半径」が求まるんだね。
円錐の底面の半径を求める問題①
下の円錐の底面の半径を求めなさい。
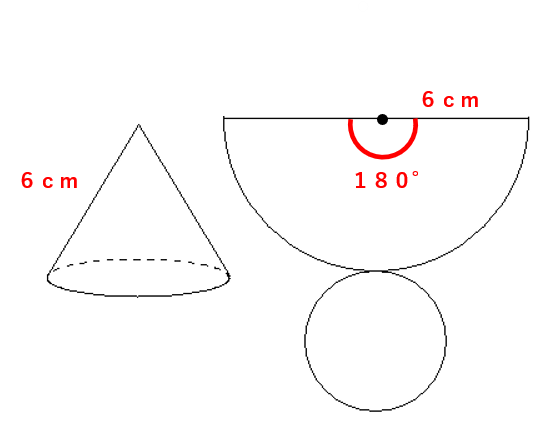
STEP1 弧の長さを求めよう。
おうぎ形の弧の長さを求める公式は次の通りだったよね。
直径×円周率×\(\frac{中心角}{360}\)
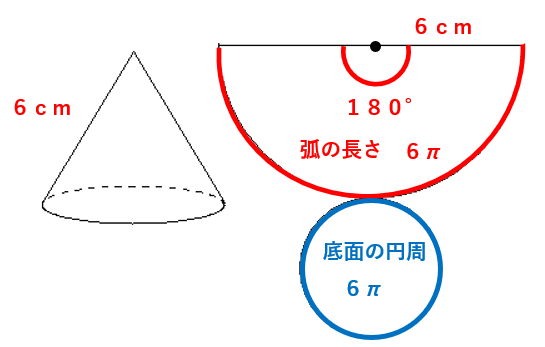
おうぎ形の半径(母線)が6cm、中心角180°で円周率はπを使うから、式に当てはめると
直径×円周率×\(\frac{中心角}{360}\)
=12×π×\(\frac{180}{360}\)
=6π (cm)
おうぎ形の弧の長さは6πだとわかったね。ということは、底面の円周も6πだとわかるね。
STEP2底面の円の半径を求める
底面の円周が6πだから、半径も求められそうだよね。円周の求め方は次の通りだったね。
円周=直径×円周率
この式に、円周6π、円周率πを代入すると
6π=直径×π
上の式から直径=6であることがわかるね。だから、底面の半径は6÷2=3cmということだね。
円錐の底面の半径を求める問題②
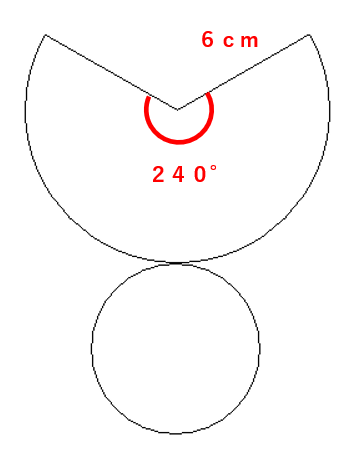
下の図は円錐の展開図である。円錐の底面の半径を求めなさい。
STEP1 弧の長さを求めよう。
おうぎ形の弧の長さを求める公式は次の通りだったよね。
直径×円周率×\(\frac{中心角}{360}\)
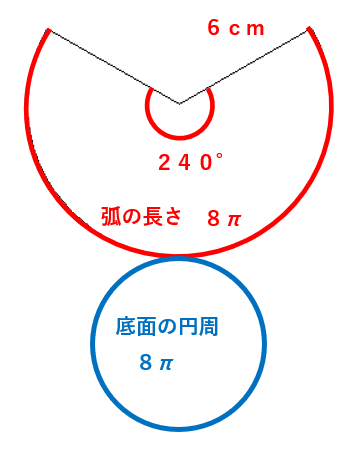
おうぎ形の半径(母線)が6cm、中心角240°で円周率はπを使うから、式に当てはめると
直径×円周率×\(\frac{中心角}{360}\)
=12×π×\(\frac{240}{360}\)
=8π (cm)
おうぎ形の弧の長さは8πだとわかったね。ということは、底面の円周も8πだとわかるね。
STEP2底面の円の半径を求める
円周の求め方は次の通りだったね。
円周=直径×円周率
この式に、円周8π、円周率πを代入すると
8π=直径×π
上の式から直径=8であることがわかるね。だから、底面の半径は8÷2=4cmということだね。
円錐の母線と底面の半径と中心角の関係(裏ワザ)
実は、円錐の「母線」「おうぎ形の中心角」そして「底面の半径」には、ある関係式が成り立っているんだ。
さっき紹介した例題と2つの問題で求めた「母線」「おうぎ形の中心角」「底面の半径」を下の表にまとめてみるよ。
| 例題 | 問題① | 問題② | |
| 母線 | 6cm | 6cm | 6cm |
| 中心角 | 120° | 180° | 240° |
| 底面の半径 | 2cm | 3cm | 4cm |
どうかな?
なんとこの3つは、「母線×\(\frac{中心角}{360}\)=底面の半径」
という関係が成り立っているね。
この関係を利用すれば、「母線」「おうぎ形の中心角」「底面の半径」のうちどれか2つまでが分かっていれば、簡単にのこりのひとつを求めることができるね。
円錐の展開図と中心角の求め方
さっきは、「母線と中心角」から「底面の半径」を求めたね。
それでは今回は、「母線と底面の半径」から「中心角」を求めてみよう。
問
下の円錐を展開したとき、側面の中心角を求めなさい。
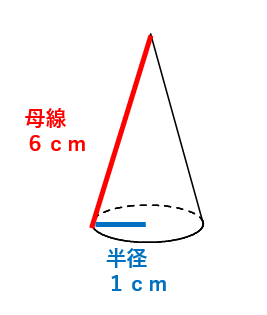
円錐の展開図は次のようになるよね。おうぎ形の中心角がわからないからx°にしたよ。
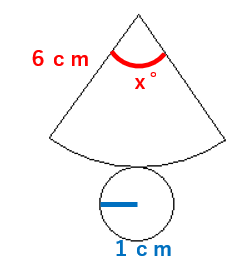
STEP1 おうぎ形の弧の長さをxを使って表そう。
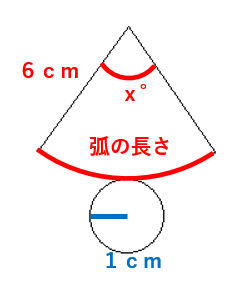
おうぎ形の弧の長さを求める公式は次の通りだったよね。
直径×円周率×\(\frac{中心角}{360}\)
おうぎ形の半径(母線)が6cm、中心角x°で円周率はπを使うから、式に当てはめると
直径×円周率×\(\frac{中心角}{360}\)
=12×π×\(\frac{x}{360}\)
STEP2 底面の円の円周を求めよう。
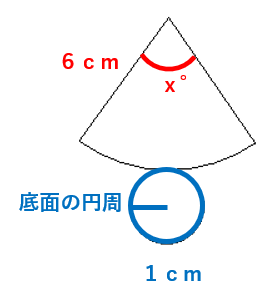
円周の求め方は次の通りだったね。
直径×円周率
この式に、直径2、円周率πを代入すると
直径×π
=2×π
=2π (cm)
STEP3 方程式をたてて中心角を求めよう。
円錐の展開図では、おうぎ形の弧の長さと底面の円周が等しくなるので、STEP1とSTEP2の式で方程式を作ろう。
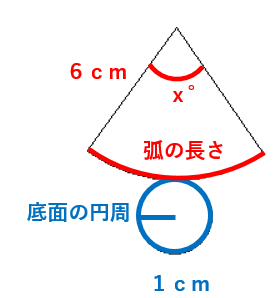
おうぎ形の弧の長さ=底面の円の円周 になるから
12×π×\(\frac{x}{360}\)=2π
という方程式をたてることができるよ。これをxについて解けば、中心角が求まるってこと。
12×π×\(\frac{x}{360}\)=2π
\(\frac{x}{30}\)=2
\(\frac{x}{30}\)×30=2×30 ←両辺に30をかけるよ。
x=60
xは中心角だったから、おうぎ形の中心角は60°と求められるよ。
「円錐の展開図の半径・弧の長さ・中心角の求め方」まとめ
円錐の「母線と中心角」から「底面の半径」を求める方法
1.展開図を書いて、おうぎ形の弧の長さを求める
公式:直径(母線×2)×円周率×\(\frac{中心角}{360}\)
2.おうぎ形の弧の長さと、底面の円周は等しいことから、底面の半径を求める。
公式:円周=直径×円周率
円錐の「母線と底面の半径」から「中心角」を求める方法
- おうぎ形の弧の長さをxを使って表す
公式:直径(母線×2)×円周率×\(\frac{x}{360}\) - 底面の円の円周を求める
公式:直径×円周率 - 1の式と、2で求めたもので方程式をたててx(中心角)を求める
円錐の「母線」「おうぎ形の中心角」「底面の半径」の3つは「母線×\(\frac{中心角}{360}\)=底面の半径」という関係で成り立っている
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。