「平均値・中央値・最頻値」とは?データ分布の特徴・表し方を解説
中学1年生の「データ分布の特徴・表し方」で学習する「平均値・中央値・最頻値・範囲」とはどういうものかを、例を使いながら分かりやすく解説するよ。
それぞれのデータの表し方ごとの例題も紹介していくよ。
平均値とは
「平均」っていう言葉はよく聞くよね。
「テストの平均点」とか「平均気温」とか。
中学1年生の数学「データの分布の特徴・表し方」の学習では、「平均値」とはどういうものかについて勉強するよ。
「平均値って、平均とは違うの?」と疑問に感じる人がいるかもしれないね。
「平均」と「平均値」は同じものだと思ってOKだよ。
みんながよく使う「平均」と同じように、「平均値」 とは、 「データの合計」 を 「全体の数」 で 割ったもののことだよ。
あるクラスのテストの平均点を出すときも、そのクラスの生徒みんなの点数をたして、生徒の人数で割るよね。それと同じだよ。
それでは実際に平均値を求めてみよう。
例題 次のデータの平均値を求めなさい。
3、4、5、5、6、7、7、7、10、11
まず、「データの合計」を求めるよ。
データの合計を求めるには、それぞれの数値をすべて足せばいいよね。
3+4+5+5+6+7+7+7+10+11=70
平均値を求めるには、「データの合計」を「全体の数」で割ればいいね。
「全体の数」とは、いくつデータがあるかということだよね。
例題では全部で10個のデータがあるから、「10」で割ろう。
70÷10=7
平均値は7であることがわかったね。
平均値 まとめ
- 平均値とは、「データの合計」 を 「全体の数」 で 割ったもののこと。
- データの数値すべてを合計して、データ全体の数で割って求める。(例)20人のクラスのテストの点数の合計点が1200点だった場合、1200÷20=60で、平均値は「60」。
中央値(メジアン)とは
中央値っていうのは、その名前のまま「中央の値」のこと。
データを小さい順に並べたときに、「中央にある値」のことだよ。
「メジアン(median)」とは、英語で「中央」という意味をもつ言葉なんだ。
例題で見てみよう。
例題 次のデータの中央値を求めなさい。
3、4、5、6、7、7、11
データは全部で7個あって、データを小さい順に並べたとき、ちょうど真ん中にある「中央の値」は4番目の「6」だね。
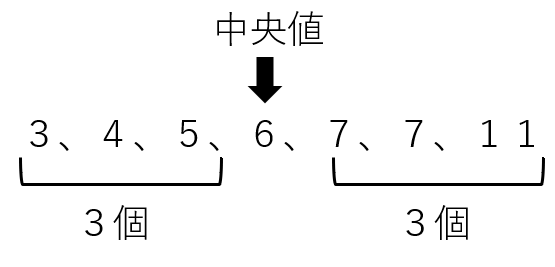
だから中央値は「6」となるよ。
かんたんだね。
データの数が奇数で、今の問題のように、ちょうど真ん中になるデータがあれば、いいんだけれど、こんな場合もあるよ。
例題 次のデータの中央値を求めなさい。
3、4、5、6、7、7、7、11
データは8個あるね。
「中央の値」はどれかなと考えるんだけど、データの数が偶数なので、きれいに4個ずつ半分に分かれてしまって、「中央の値がない!」ってなってしまうね。
このような場合、「中央の値」は、「6と7の間」になるんだよ。
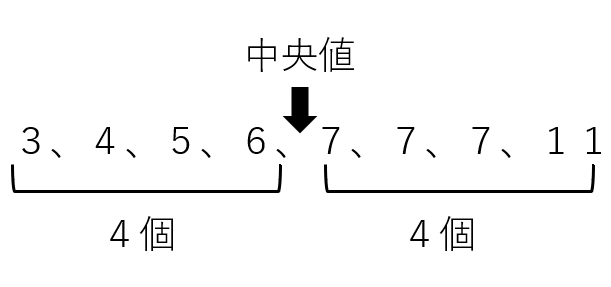
だから、答えは(6+7)÷2=6.5。中央値は6.5と求められるよ。
こんな問題のように、データが偶数個のときは、ちょっと注意が必要だね。
中央値 まとめ
- 「中央値」とは、データを小さい順に並べたときに中央にある値
- データが偶数個の時は注意が必要。
真ん中にある2つの値を足して2で割ろう。
中央値は一番テストに出やすいので、もう少し問題に挑戦してみよう。
中央値を求める問題
(1)次の値は5人のテストの点数です。中央値を求めなさい。
8、5、3、4、10
中央値っていうのは、小さい順に並べたときの中央の値だったよね。だから、まずはテストの点数を小さい順に並べないといけないよ。
例題のデータを小さい順に並べると
3、4、5、8、10 になるね。
そうすると、ちょうど中央にある「中央の値」は5だとわかるね。
よって中央値は5だよ。
中央値の問題には、次のようなパターンもあるよ。
(2)表はAさんの100m走9回の記録です。中央値を求めなさい。
| 階級(秒) 以上 未満 | 度数 (回) |
| 15.5 16.0 | 1 |
| 16.0 16.5 | 4 |
| 16.5 17.0 | 2 |
| 17.0 17.5 | 1 |
| 17.5 18.0 | 1 |
「中央にある値」といっても、ある階級の度数がいくつかが分かっているだけで、実際に度数それぞれが「いくつか」はわからないよね。
そうすると、「中央にある値」がいくつかもサッパリわからないよね。
こんなパターンの中央値を答える問題のときは、「階級の真ん中の数値をデータとして使う」というルールがあるんだ。
たとえば、「16.0~16.5」の階級地の真ん中の数値は「16.25」だよね。
「16.0~16.5」の階級にあるデータは、「16.25」だったとして考える、ということだね。
ちなみにこの「階級の真ん中」のことを階級値というよ。
さっきの表に階級値を加えると次のようになるよ。
| 階級(秒) 以上 未満 | 階級値 (秒) | 度数 (回) |
| 15.5 16.0 | 15.75 | 1 |
| 16.0 16.5 | 16.25 | 4 |
| 16.5 17.0 | 16.75 | 2 |
| 17.0 17.5 | 17.25 | 1 |
| 17.5 18.0 | 17.75 | 1 |
「16.0~16.5」の階級の度数は「4」だよね。
つまり、この階級に当てはまるデータが4つあるよ、ということだよね。
この4つのデータは階級値の「16.25」として考える、というわけだね。
そのようにすべてのデータを階級値とおきかえて、9回分のデータの記録を小さい順に並べると次のようになるよ。
15.75、16.25、16.25、16.25、16.25、16.75、16.75、17.25、17.75
これなら中央値は「16.25」になるということがわかるね。
とはいえ、いちいち階級値とおきかえて並び替えるのは大変だね。
慣れてきたら最初の表から求めることもできるよ。
慣れたらやってみよう!
表を読み取ってかんたんに中央値を求める方法
たとえば、9回分のデータということは、真ん中のデータは9÷2の「4.5回目」になるよね。
本当なら回数なので、小数点を使ってしまうとおかしくなるけれど、つまりは「4回めと5回目の間」と考えてもらえればわかりやすいかな。
「15.5~16.0」の階級にすでに1回目のデータがあるので、4回目と5回目の間のデータは、「16.0~16.5」の階級になるよね。
だから、中央値は「16.0~16.5」の階級だということになって、階級値の「16.25」をすぐに求めることができるんだ。
最頻値(モード)とは
最頻値(さいひんち)は、その字のままで、「最も頻繁な値」のこと。
一番多く出現している値のことを最頻値っていうんだ。
「モード(mode)」は、フランス語で「流行」という意味なんだ。
流行っているものは、よく見かけるよね。
だから、最頻値のことを「モード」と呼ぶよ。
多分、平均値や中央値よりも理解しやすいと思うよ。
例題 次のデータの最頻値を求めなさい。
3、4、5、6、7、7、7、11
一番多く出現している値は7だよね。7だけ3回も出現しているからね。だから、最頻値は7と求められるよ。
最頻値(モード) まとめ
・一番多く出現している値のこと
範囲(レンジ)とは
範囲っていうのは、最大値から最小値を引いた値のことだよ。
「最大値−最小値」と覚えよう。
「レンジ(range)」は英語で「範囲」という意味だよ。
たとえば、あるクラスのテストの点数の最高得点が98点で、最低点は20点だったとするよ。
そうすると、そのクラスのテストの得点の範囲って、20点~98点までの78点分だよね。
これは、最高得点の98点から、最低点の20点を引けば計算することができるよね。
例題 次のデータの範囲を求めなさい。
3、4、5、6、7、7、7、11
最大値(もっとも大きい値)は11
最小値(もっとも小さい値)は3
だから、範囲は11−3=8と求められるよ。
範囲(レンジ) まとめ
・最大値から最小値を引いた値
データの特徴と表し方 まとめ
データの特徴と表し方 まとめ
- 「平均値」とは、「データの合計」 を 「全体の数」 で 割ったもののこと。
データの数値すべてを合計して、データ全体の数で割って求めることができる。 - 「中央値(メジアン)」とは、データを小さい順に並べたときに中央にある値。
データが偶数個の時は注意が必要で、真ん中にある2つの値を足して2で割って求める。 - 「最頻値(モード)」とは、一番多く出現している値のこと。
- 「範囲(レンジ)」とは、最大値から最小値を引いた値のこと。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


