一次式の加法・減法・乗法・除法の解き方を解説（項と係数とは）

中学１年の数学で学習する「一次式」について、「項」とは何か、「係数」とは何か、一次式の加法と減法のやり方と注意点、乗法・除法の解き方を実際に例題を使って解説するよ。

一次式の加法・減法・乗法・除法の解き方を解説 （項と係数とは）のPDF（16枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 項とは
• 係数とは
• 一次式とは
• 一次式の加法と減法
• 一次式の乗法と除法
• 一次式の問題例
• 一次式のまとめ

項とは

教科書

項とは＋で結ばれた数のこと

【例１】

３＋４ｘ

この式の項は「３」と「４ｘ」だよ。

【例２】

２ｘ＋３

この式の項は「２ｘ」と「３」だよ。

【例３】

４ｘ＋１

この式の項は「４ｘ」と「１」だよ。

たしかに、教科書の説明どおり、それぞれ「＋で結ばれた数」だね。
「なんだ、項を見つけるのなんてカンタンじゃん」と思った人もいるんじゃないかな？
では、たとえば次の場合はどうだろう。

項で間違えやすい問題

次の式の項は何になるかな？

７ｘ－２ｙ

たろう

７ｘと２ｙじゃないの？

それは間違いなんだ。
だって、項は「＋で結ばれた数」のことだったよね。
この式は、「－（マイナス）」で結ばれていて、「＋（たす）」で結ばれていないから、項ではないんだ。

でも、項を探さなきゃいけないよね。
なので、この式をちょっとアレンジして、項がある状態にするよ。

項は、「＋で結ばれた」ものなんだから、この式を「－（マイナス）」ではなく「＋（プラス）」で結びなおせばいいんだよ。

次のように式をアレンジすれば、「＋で結ばれている」状態にすることができるよ。

　７ｘ　　－２ｙ

＝７ｘ＋（－２ｙ）

何が起きたかわからない！と思ったら読もう

たとえば「７－２」を考えてみよう。
答えは５だね。

７ー２って、「７」から「２を引く」とも考えられるけれど、「７」に「－２を足す」という風に考えることもできるよね。

たとえるなら、カードゲーム。プラスポイントのカードと、マイナスポイントのカードがあって、配られたカードの合計ポイントで勝負するとゲームがあるとしよう。

もしそのゲームをしていて、「プラス７」と、「プラス２」のカードがあったのに、「プラス２」のカードを相手に取られちゃったら、ポイントはどうなる？

そう、「７－２＝５ポイント」になるよね。

では、「プラス７」のカードを持っていたところに、もう一枚カードを受け取ったら「マイナス２」のカードだったらポイントはどうなる？

そう、「７－２＝５ポイント」という計算をするよね。
これって、つまりは「７＋（－２）」をしているんだよ。だって、「－２」のカードを「加えて」いるでしょ。

「プラスの数を引く（７－２）」と、「マイナスの数を足す（７＋（－２）」は答えが一緒になるね。

なので、項を作り出すために、式をアレンジすることができるんだよ。

７ｘ－２ｙ

＝７ｘ＋（－２ｙ）

という形にできたら、もう項を見つけるのはカンタンだね。
「プラスで結ばれた数」を探せばいいんだから。

項は「７ｘ」と「－２ｙ」ということがわかるね。

たろう

「－」で結ばれているときには、式をアレンジする必要があるから要注意だね。

係数とは

係数とは、文字に係っている（かけられている）数字のことだよ。
「係」という漢字は、糸で結びついている様子を表しているんだ。
「項」は、その場（式の中）に一緒にいる別々の家族だったとしたら、
「係数」は結婚して家族になっているイメージかな。

例えば、
３ｘだったら、係数は３。
－２ｙだったら、係数は－２。
という感じ。項よりもわかりやすいね。

じゃあ、少しレベルアップしてみよう。

係数で間違えやすい問題

係数で間違えやすい問題を３問紹介するね。

①ｘの係数は？

②－ｙの係数は？

③\(\frac{ｘ}{３}\)の係数は？

文字に係っている数字が係数だったよね。

①は・・・「あれ？数字なんてないよ」と思う人もいるんじゃないかな？

だけど「ｘ」は丁寧に書くと「１ｘ」のことだったね。
だから係数は「１」になるよ。

同じように②を考えてみよう。「－ｙ」を丁寧に書くと「－１ｙ」だから、係数は「－１」だね。

じゃあ、③の分数の場合はどうなるのかな？

\(\frac{ｘ}{３}\)も同じように、丁寧に書くと\(\frac{１ｘ}{３}\)だから、係数は\(\frac{１}{３}\)だよ。

項と係数を組み合わせた問題

「項と係数、両方求めてみよう」という問題を紹介するね。

【例１】ｘ－３ｙの項と係数を求めよう。

「－」で結ばれているから注意が必要だったね。

まず

ｘ－３ｙ
＝ｘ＋（－３ｙ）

という形にすると、項は「ｘ」と「－３ｙ」であることがわかるよね。

係数は、文字にかけられている数だから、

「ｘ」の係数は「１」
「－３ｙ」の係数は「－３」

だね。

一次式とは

１年生で勉強する一次式とは何だろう？
ひとことで説明すると、「文字が1つだけかけられている式」のことだよ。

一次式があるなら・・・そう、文字が２つかけられている二次式とか、文字が３つかけられている三次式もあるよ。

中学２年生で二次式、高校生で三次式を学習するよ。

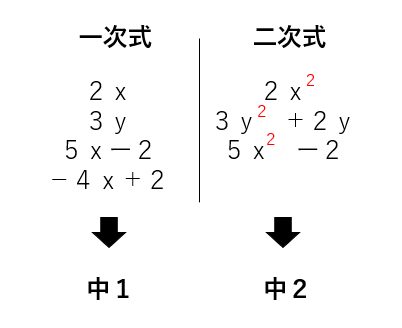
教科書に書いてある「一次の項」とは何かというと、
「２ｘ」や「３ｙ」のように文字が１つだけの項のことなんだ。
「数の項」とはなにかというと、そのまま「数字だけの項」のこと。

さっきの「一次式の条件」をもう一度確認してみるよ。

①「一次の項」だけの式（例：２ｘ、３ｙ）

②「一次の項」と「数の項」の和（例：５ｘ－２、－４ｘ＋２）

①は、文字が1つだけの「一次の項」だけの式なら、文字は１つしかかけられていないからセーフだね。

②ももちろん、一次の項と、数の項だけの式なら、文字は1つしかかけられていないからセーフだね、

一次式に関する問題

次のうちで一次式はどれですか？

ア：－８ｘ
イ：ｘ^２＋１
ウ：２ａ＋８
エ：\(\frac{２}{５}\)ａ－２
オ：ｘｙ＋４　

【解答】

ア・ウ・エ

【解説】

イは「ｘ^２」という項があるので、二次式になるよ。
オも、「ｘとｙ」の２つの文字がかけられているので、二次式になるよ。
※ｘ＋ｙ＋４だったら一次式だけどね。

一次式の加法と減法

ここまでで、一次式とはどんな式かがわかったかな？
それでは、実際に一次式の加法や減法の計算をしてみよう。

まず次の問題を考えてみよう。

２ａ＋３ａ

先に答えを言ってしまうと

２ａ＋３ａ＝５ａ

たろう

なんで２ａ＋３ａ＝５ａになるの？

２ａ＋３ａ＝５ａになる理由

図形を使って①～③の順に考えてみよう。

①２ａってａ×２だよね。
たとえば、「縦がａ」で「横が２」の長方形の面積は「２ａ」ということになるよね。

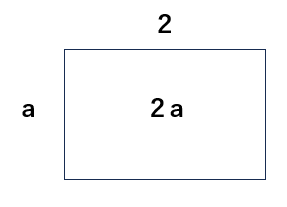
②３ａってａ×３だよね。
たとえば、「縦がａ」で「横が３」の長方形の面積は「３ａ」ということになるよね。

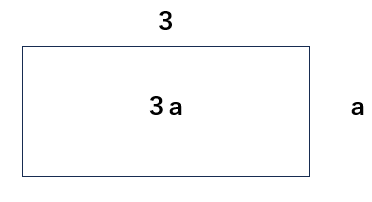
③２ａ＋３ａは２つの長方形の面積を足したらいいよね。そうすると、下の図のように、縦ａで横が２＋３＝５の長方形になるから、面積はａ×５＝５ａだね。

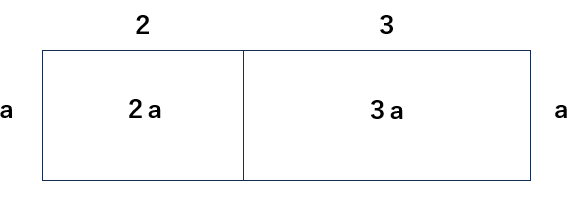
２ａ＋３ａ＝５ａになることが説明できるね。

同じように計算してみよう。

【例１】３ｘ＋４ｘ＝（３＋４）ｘ＝７ｘ

【例２】７ａ＋３ａ＝（７＋３）ａ＝１０ａ

たろう

文字の前の係数を足せばいいんだね。

２ａ＋３ｂや２ａ＋３は計算できない

さっき２ａ＋３ａ＝５ａになることはわかったんだけど、次の計算はどうなるだろうか？

２ａ＋３ｂ

答えは「これ以上計算できない」だよ。

たろう

なんで計算できないの？

２ａ＋３ｂが計算できない理由

さっきは２ａと３ａで縦の長さが両方ともａの長方形だったけど、２ａ＋３ｂは縦の長さがａとｂでバラバラだから、面積を合計することできないよね。

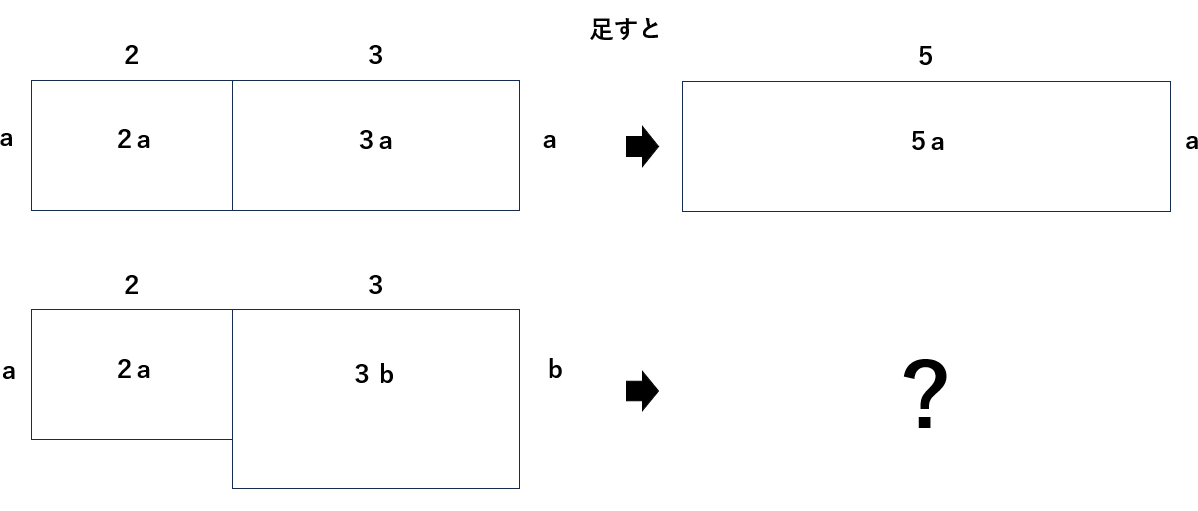
同じ理由で２ａ＋３も計算できないよ。

一次式の加法と減法のポイント

一次式の加法と減法のポイントは次の通りだよ。これだけはしっかり頭にいれておこう。

一次式の加法と減法の計算練習

次の問題に挑戦してみよう。

（１）４ｘ＋７＋５ｘ－６

＝４ｘ＋５ｘ＋７－６
＝（４＋５）ｘ＋１
＝９ｘ＋１　　　　　　

（２）－３ａ＋１－２ａ－３

＝－３ａ－２ａ＋１－３
＝（－３－２）ａ－２
＝－５ａ－２

くまごろう

できたかな？じゃあ次は（　）がある計算に挑戦だ！

（　　）＋（　　）の場合は（　　）の中身をそのまま書くだけでいいよ。

　（３）（２ｘ＋３）＋（－２ｘ＋４）

＝２ｘ＋３－２ｘ＋４ ←「＋」を省くだけ
＝２ｘ－２ｘ＋３＋４
＝（２－２）ｘ＋７　　　　　　　　　
＝０ｘ＋７←０ｘ＝０
＝７

（　　）－（　　）の場合は「＋」に変えて考えよう。

　（４）（２ｘ＋３）－（－２ｘ＋４）

＝（２ｘ＋３）＋（＋２ｘ－４）
※「－」を「＋」に変えたら、後ろの符号が変わるよ。
＝２ｘ＋３＋２ｘ－４
＝２ｘ＋２ｘ＋３－４
＝（２＋２）ｘ－１
＝４ｘ－１　

一次式の乗法と除法

一次式の乗法と除法は簡単だよ。ポイントは「数字同士、文字同士かけたり、割ったりする」だけ。

（例１）４ａ×３＝１２ａ

（例２）８ｘ÷（－２）＝－４ｘ

（例３）４ｘ÷（－\(\frac{２}{３}\)）
　　　　＝４ｘ×（－\(\frac{３}{２}\)）
　　　　＝－６

分配法則を使った問題

一次式の乗法は簡単なんだけど、分配法則がかかわってくると難易度がアップするよ。

例えば次の問題を考えてみよう。

【例】２（ｘ＋３）

２（ｘ＋３）は、丁寧に書いたら２×（ｘ＋３）だよね。

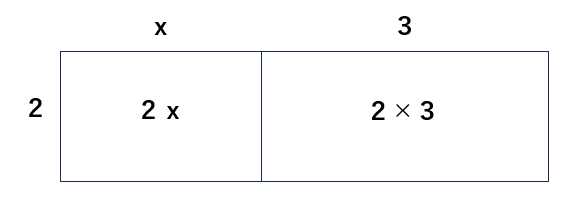
これを図形で考えると、縦が「２」で横が「（ｘ＋３）」の長方形の面積を求めることと同じ計算になるね。

下の図を見てわかるように、面積は「２×ｘ」＋「２×３」になるよ。
さっきの分配法則の式と比べてみると、同じだということがわかるね。

　２（ｘ＋３）
＝２×ｘ＋２×３
＝２ｘ＋６

一次式の問題例

一次式の問題に挑戦してみよう。

一次式の基本問題

（１）２ｘ＋３－５ｘ＋２

＝２ｘ－５ｘ＋３＋２
＝（２－５）ｘ＋３＋２
＝－３ｘ＋５

（２）（－２ｘ＋１）＋（ｘ＋１）
＝－２ｘ＋１＋ｘ＋１
＝－２ｘ＋ｘ＋１＋１
＝（－２＋１）ｘ＋１＋１
＝－ｘ＋２

（３）（－２ｘ＋１）－（ｘ＋１）

＝（－２ｘ＋１）＋（－ｘ－１）←「－」を「＋」にすると符号が変わる
＝－２ｘ＋１－ｘ－１
＝－２ｘ－ｘ＋１－１
＝（－２－１）ｘ＋１－１
＝－３ｘ　

（４）３ｘ×（－４）

＝－１２ｘ

（５）－３ｘ×（－２）

＝６ｘ

（６）３（ｘ－４）

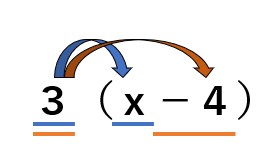
＝３×ｘ＋３×（－４）
＝３ｘ－１２←文字と数字の足し算・引き算はできない

一次式の応用問題

２（ｘ＋１）－３（ｘ－２）

この問題を解くときは、前半と後半に分けよう。

①まず前半は２（ｘ＋１）。

分配法則で（　　）を外すと

２（ｘ＋１）
＝２ｘ＋２になるね。

②後半は－３（ｘ－２）。

分配法則で（　　）を外すと

－３（ｘ－２）
＝－３ｘ＋６になるね。←－３×（－２）だから「＋６」になるよ。

準備が完了したので計算してみよう。

２（ｘ＋１）－３（ｘ－２）

＝２ｘ＋２－３ｘ＋６
＝２ｘ－３ｘ＋２＋６
＝－ｘ＋８

まとめ

「項」や「係数」とは何かわかったかな。

一次式の計算のやり方は中学２年生と３年生はもちろん、高校でも使う知識だよ。
だから、今のうちに完璧にしておこうね。

一次式の計算で気を付けるポイントを下にまとめたよ。

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。