「不等号」「絶対値」をわかりやすく解説（テスト対策ポイント）
yuminekoこのページでは、中学数学「数の大小」を学習するときに登場する「不等号・絶対値」というものが何かを解説するよ！
数の大小とは
「数の大小」とは、そのまま「ある数が、他の数と比べて大きいか小さいか」を考えることだよ。
他の数より大きいか小さいか・・・って、
今更！？？
くまごろう それが、中学数学では「負の数（マイナスの数）」が登場しているよね。
だから、数の大小を考えるときも、単純じゃなくなってくるんだ。
ザックリいうと
中学数学で数の大小を学ぶ理由は・・
マイナスの数の場合に「どちらの数が大きいのか」を間違えないように注意しよう！ということ
くまごろうある2つの数があるとき、どちらが「大きい数か」は分かるかな？
えっ
そんなのカンタンだよ。
例えば、5と7だったら
7の方が大きい数だよね。
そのまま「大きい数字の数」を選べばいいんでしょ。
くまごろう小学校の算数までだったらそうだね。
でも、中学数学では、負の数（マイナスの数）が登場しているから、「見かけの数」で考えるだけだとダメなんだ。
さっきの例でいうと、
−5と−7だったら、どちが「大きい数」か分かるかな？
5と7なら、7の方が大きい数字だから・・
・・あれ？？
くまごろうそう。
7の方が大きい数字だけど、負の数では、「大きい数字」＝「大きい数」ではないんだ。
数の大小は、数直線を使うと一目瞭然！
くまごろうそれぞれの数を数直線で表してみよう。
数直線では、「右に行くほど数は大きくなって、左に行くほど数は小さくなる」 よ。
−7は、−5よりも左側にあるね。
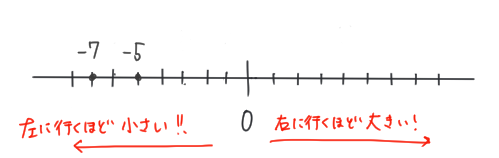
ということは、−7と−5では、−5の方が数が大きいんだ！！
くまごろう正の数では、「0から離れれば離れるほど（右に行けばいくほど）」数はどんどん増えていくよね。でも、負の数では、「0から離れる」ということは、0にどんどん遠くなっていくんだから、その数は「小さく」なっていってしまうということだね。
負の数（マイナスの数）では、数字が大きいほど「小さな数」になる！
不等号とは
ザックリいうと
「どっちが大きいか」を表す記号！
くまごろう不等号のマークは見たことあるんじゃないかな？
＝ のマークは「等しい」ということを表すよね。
\(3＋5＝8\)
「3と5を足したものは、8と等しい」ということ！
くまごろうこの「＝」のことは「等号」と呼ぶんだ。
「等しい」ことを表す「記号」だからだね。
不等号はというと、こんな記号を使うよ。
＜
＞
不等号は、「大きく口が開いているほう」が「大きい」ということを表すよ。
例えば、
A＜Bだったら、
「BはAよりも大きい」ということ。
A＞Bだったら、
「AはBよりも大きい」という意味なんだ、
くまごろうどうして「不等号」という名前かというと・・
「どちらかが大きいことを表す」わけだから、
つまり「2つの数は等しくない」ということだよね。
そうか！
「等しくない」ことを表す「記号」だから、「不等号」なんだ！
不等号はどうやって「読む」の？
\(2＜5\)
「2 小なり 5」
\(5＞2\)
「5 大なり 2」
と読むよ！
3つ以上の数の大小を不等号で表すには？
3と5と7を不等号で表してみるよ。
小さい順なら、
\(3＜5＜7\)
大きい順なら、
\(7＞5＞3\)
と表すよ。
\(3＜7＞5\)
というように、「大きい」や「小さい」の向きを混ぜて使うことはしないので注意！
絶対値とは
教科書にはなんて書いてあるの？
くまごろう実際に数直線で見てみよう。
「スタート地点」から、「東」と「西」に分かれている数直線で考えてみよう。
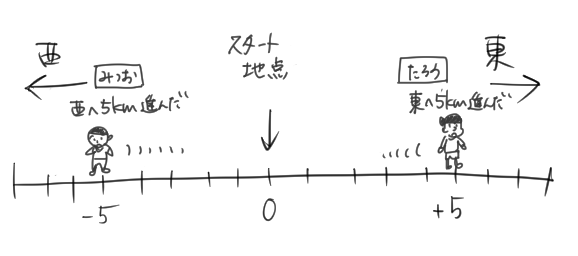
くまごろう みつお君は「西」へ5km、たろう君は「東」へ5km進んだとするよ。
このとき、数直線で表すと
みつお君は「−5」で、たろう君は「＋5」になるね。
でも、みつお君はスタート地点から「5km進んだ」わけで、たろう君と「歩いている距離は同じ」だよね。
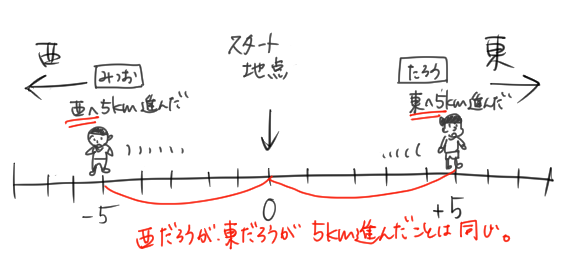
くまごろうこのように、「絶対値」というのは、原点（スタート地点・基準の点）から「どのぐらい距離があるか」ということを表すことなんだ。
「絶対」という言葉は、
「絶対約束だよ！」と使うように、「必ず」というイメージが強くないかな？
実は「絶対」には、「対立することを絶つ」という意味もあるんだ。
つまり、「対立する（比べる）ことを絶つ（やめる）」ということ。
なので、「＋」とか「−」とか比べることなく、
ただ単に「それが原点からどのくらい動いたのか」で考える ということなんだ。
くまごろうまぁ、ムズかしく考えずに、
＋5の絶対値は「5」、−5の絶対値も「5」
つまり、「符号をとってしまうだけでOK」と考えても大丈夫だよ。
でも、一体なんのためにこんな面倒くさいことまで考えるの？
絶対値は、今ではまだ「一体何に役立つの？」とピンとこないけど、この先の高校数学や複雑な学習で必要になってくるよ。
くまごろう実は、「負の数の大小」を見分けるときにも早速「絶対値」が役に立つんだよ。
−5と−7、どちらが大きい数字かを考えるときに、「負の数では、数字が大きい方が小さい数になる」のがポイントだったよね。
そうか、この「数字が大きい」というのは、「絶対値が大きい」ということだったんだ！
つまり、負の数の大小を考えるときは、数直線で表さなくても、「絶対値が大きい」ほど「数は小さくなる」ということ。
絶対値を見れば、どちらが大きい数なのか、小さい数なのか一目瞭然ということだね。
yuminekoもちろん、正の数の場合は、「絶対値が大きい」ほど「数は大きくなる」よ！
絶対値の記号
絶対値の記号には、「｜｜」のように、2本の縦線を使うよ！
｜5｜は「5の絶対値」、
｜−5｜は「−5の絶対値」という意味になるよ。
こういう問題が出る！
yumineko実際の問題は、こういう風に出てくるよ
数直線を使って、数の大小を不等号で答えるタイプ
数直線を利用して、次の各組の数の大小を、不等号を使って表しなさい。
（1）\(−6 、＋8\)
（2）\(−3、−9\)
【考え方】
①まずは それぞれの数字を
数直線の上に記入しよう！
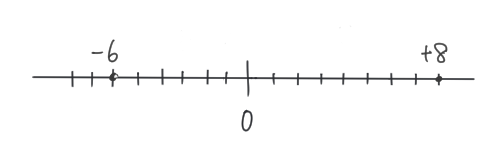
②それぞれの数字のうち、
左側にあるものほど「小さい数」。
（右側にあるものほど「大きい数」）
ということは、左側にある「−6」は、右側にある「＋8」よりも小さい数ということだね。
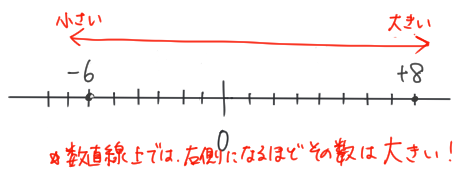
小さい数順（または大きい数順）に、
不等号の記号「＜」（または「＞」）を使って書こう
こ答え
（1）−6＜＋8
※＋8＞−6でも正解
（2）−9＜−3
※−3＞−9でも正解
くまごろう小さい順に表したときは−6＜＋8になるし、大きい順に表したときは＋8＞−6になるね。
これはどちらでも正解だよ。
不等号の記号の「開いている方」が大きい数の方になるようにだけ注意してね！
これでOK！
数の大小を不等号を使って表わすタイプ
次の各組の数の大小を、不等号を使って表しなさい。
（1）−7、−4
（2）＋6、＋11
さっきの問題と違うのは、「数直線を使って」という部分がないことだね。
つまり、「数直線をヒントにできない」ということ。
このとき役に立つのが「絶対値」なんだ。
①数字の組み合わせが、
「正の数」なのか「負の数」なのか見る
（1）をみてみよう。
\(−7\)と\(−4\)の組み合わせなので、「負の数」だね。
（2）は、
\(＋6\)と\(＋11\)なので、「正の数」だね。
②絶対値で数の大小を判断する！
「正の数」のときは、絶対値が大きいほど「数は大きい」よ。
「負の数」のときは、絶対値が大きいほど「数は小さい」ね。
つまり、
（1）は負の数なので、絶対値が大きいほど数は小さくなる。
−7の絶対値は「7」
−4の絶対値は「4」。
絶対値が大きい−7の方が−4よりも小さい数ということがわかるよ。
あとは、不等号で順番に書けばOK！
（2）は正の数なので、絶対値が大きいほど数も大きくなる。
＋6の絶対値は「6」
＋11の絶対値は「11」。
絶対値が大きい＋11の方が＋6よりも大きい数ということがわかる。
あとはやはり、不等号で順番に書けばOKだよ。
答え
（1）\(−7＜−4\)
※\(−4＞−7\)でも正解
（2）\(＋6＜＋11\)
※\(＋11＞＋6\)でも正解
分数で問題が出たときはどうする？
数の大小の問題では、問題に分数が登場することもあるよ。
次の各組の数の大小を、不等号を使って表しなさい。
\(-\frac{5}{8}\)，\(-\frac{2}{9}\)
分母が同じであればいいけど、分母が違う分数だと、パッとみて「どちらが大きい数」かどうか分かりにくいよね。
くまごろう分数が出た時、どうすればいいか2つの方法があるよ！
方法①通分する
分母が違って分かりにくいのだから、「通分」すればいい ね。
\(-\frac{5}{8}\)，\(-\frac{2}{9}\)だから、
通分すると
\(-\frac{45}{72}\)，\(-\frac{16}{72}\)になるね。
絶対値は\(-\frac{45}{72}\)の方が大きい。
2つは負の数なので、絶対値が大きい方が数は小さくなるね。
あとは大小に合わせて不等号で表せばOK。
答える時は通分する前のもとの分数のまま答えよう。
方法②分数を「分子÷分母」することで小数に直す！
分数を小数に直せば、どちらが大きい数字なのかハッキリする ね。
分数を小数に直したい場合は、「分子」を「分母」で割ればよかったね。
上の問題だと、
\(-\frac{5}{8}\)は「\(−（5÷8）\)」で、 \(−0.625\)。
\(-\frac{2}{9}\)は「\(−（2÷9）\)」で \(−0.222\)。（小数点第3位を四捨五入したよ）
小数に直せば、絶対値は-0.625の方が大きいって分かるね。
あとは、「負の数」では「絶対値が大きいほど数は小さい」ので、
\(-0.625＜-0.222\)
問題では分数だったから
\(-\frac{5}{8}\)＜\(-\frac{2}{9}\)が答えだよ。
答え
\(-\frac{5}{8}\)＜\(-\frac{2}{9}\)
※\(-\frac{2}{9}\)＞\(-\frac{5}{8}\)でも正解
中学数学ではココを押さえればOK！
数の大小まとめ
- 数直線では「右にいくほど」数は大きくなる。
- 数直線では「左にいくほど」数は小さくなる。
- どちらか片方が、もう片方よりも大きいことを表す記号を不等号と呼ぶ。
- A＜Bは、「AはBよりも小さい」「BはAよりも大きい」ことを表す。
- A＞Bは、「AはBよりも大きい」「BはAよりも小さい」ことを表す。
- 3つ以上の関係を表す時、＜と＞の向きを混ぜて使ってはいけない。
- 数直線上で、ある数に対応する点の「原点からの距離」を、その数の絶対値という。
- 負の数では、絶対値が大きいほど数は小さくなる。
- 正の数では、絶対値が大きいほど数は大きくなる。
- 分数を含む数の大小を答える場合の方法2つ
①通分して考える
②分数を小数に直して考える
yumineko次は「加法・減法」」の計算のコツについて解説するよ！
運営者情報
ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。
-
-
ぜひ続きもお願いします
-
ぜひ続きもお願いします
-
目次にある加法、減法のところです。
-
目次にある加法、減法のところです。
-
目次にある加法、減法のところです。
-
数の世界（数直線）の風景（HHNI眺望）は、5冊の絵本で・・・
絵本「こんとん」
絵本「みどりのトカゲとあかいながしかく」
絵本「哲学してみる」
絵本「わのくにのひふみよ」
絵本「もろはのつるぎ」母の日に臍を観つめてひふみよに
寸心忌こん・こんこんで線に生る
ぜひ続きもお願いします