「台形・平行四辺形・ひし形」の特徴と書き方(いろいろな四角形)
小学校4年生の算数で学習する「いろいろな四角形」について、台形・平行四辺形・ひし形とはどういう形なのか、それぞれの特徴をわかりやすく解説しているよ。
平行四辺形の書き方も、くわしく紹介しているよ。
「四角形」っていうのは、4本のまっすぐな線(直線)でかこまれた形のことだよね。
四角形は、その4本の直線がどんな直線かによって、いろいろな種類にわかれるんだ。
4本の直線が「平行かどうか」に注目すると、下のように3つにわけることができるよ。
- 向かい合った辺どうしが、それぞれ平行ではない
- 1組の向かい合った辺どうしが、平行(もう1組みは平行ではない)
- 2組の向かい合った辺どうしが、それぞれ平行
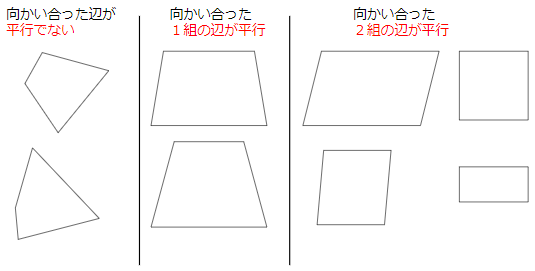
「台形」とは(1組の辺が平行)
「台形(だいけい)」っていうのは、4本の直線が「平行かどうか」で分けた3種類のうちのひとつ、「向かい合った1組の辺が平行な四角形」のことだよ。
1組の辺だけが平行になっていることがポイント。
身の回りで考えたら、跳び箱とかプリンを横から見たような形が台形だね。
台形の形は、1組の辺が平行になっているので、なんだか上に乗ることが出来そうだよね。
「踏み台」に似ているから、台形と呼ばれているんだよ。
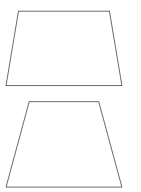
「平行四辺形」とは(2組の辺が平行)
「平行四辺形(へいこうしへんけい)っていうのは、4本の直線が「平行かどうか」で分けた3種類のうちのひとつ、「向かい合った2組の辺が平行な四角形」のことだよ。
台形は1組の辺だけが平行だったけど、
平行四辺形は2組の辺が平行になるんだ。
「2組の向かい合った辺」は、全部で4つの辺だよね。
4つの辺が平行な形だから、「平行四辺形」と呼ぶんだね。
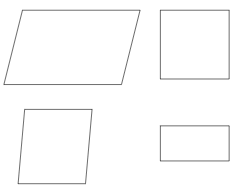
あれ?長方形や正方形も2組の辺が平行だよね。
ということは、平行四辺形のなかまってこと?
そうだね。長方形や正方形は、2組の辺が平行になっているから「平行四辺形」ともいえるよ。
平行四辺形のうち、さらに4つの角が直角だと長方形、さらに4つの辺の長さがすべて同じだと正方形になるんだ。
つまり、長方形と正方形は、平行四辺形にふくまれる特別な形というわけだね。
下の図のようなイメージだよ。
平行四辺形の特徴
向かい合った2組の辺がそれぞれ平行になったものが平行四辺形だったね。
平行四辺形には、2つの特ちょうがあるんだ。
平行四辺形の特ちょう
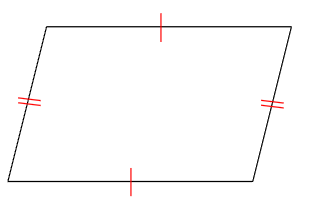
- 向かい合った辺の長さが等しい
向かい合った辺どうしの長さは、それぞれ同じだよ。
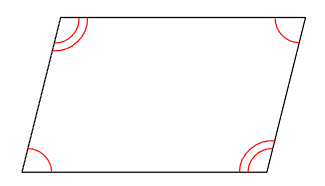
- 向かい合った角の大きさが等しい
向かい合った角の大きさも、それぞれが同じになるよ。
2組の辺がそれぞれ平行になると、2組の辺の長さはそれぞれ同じになるし、向かい合った2組の角の大きさも同じになるということだね。
台形の形をもういちど確認してみると、向かい合った辺の長さは同じではないよね。
向かい合った角の大きさも同じではないね。

平行四辺形の特ちょうを使った問題
平行四辺形の特ちょうを知っていると、まだ分からない辺の長さや、角の大きさをもとめることができるんだ。
下の四角形は平行四辺形です。
?の長さを求めなさい。
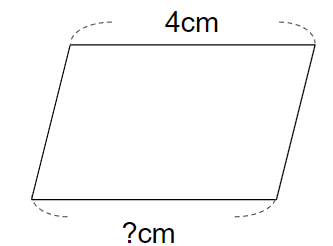
平行四辺形の特ちょうは、「向かい合った辺の長さが等しい」のだから、
?の長さは向かい合っている辺と同じ4cmになるよ。
下の四角形は平行四辺形です。
?の角の大きさを求めなさい。
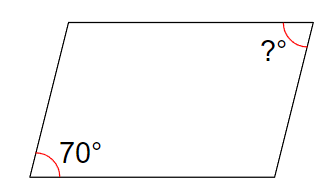
平行四辺形の特ちょうは、「向かい合った角の大きさが等しい」のだから、
?の角の大きさは向かい合っている角と同じ70°になるよ。
平行四辺形の書き方
平行四辺形の書き方をしょうかいするね。
ポイントはもちろん「平行な線」だよ。
平行な線の書き方をわすれてしまっていたら、平行な線の書き方もふく習しておくとあんしんだよ。
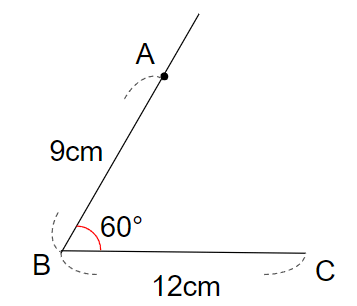
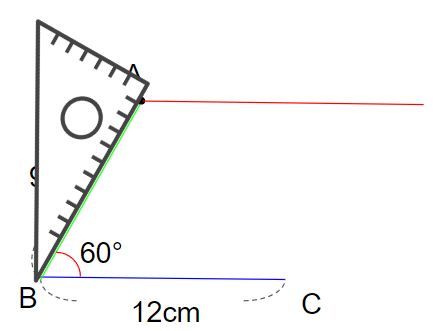
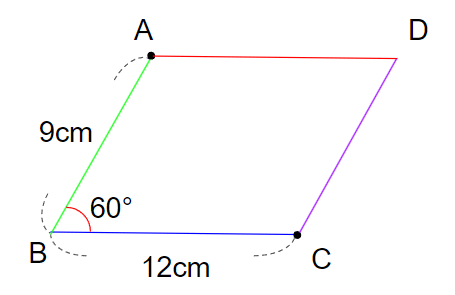
下の図のような「1辺(辺AB)が9cm、1辺(辺BC)が12cmで、その間の角の大きさが60°の平行四辺形」を作図していこう。
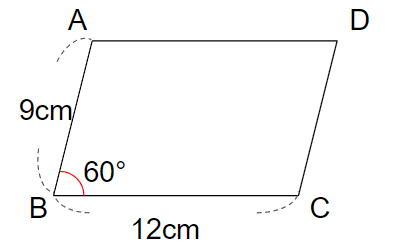
①辺BCを書こう
まず、1辺を書くよ。
今回は、辺BCを先に書いてみよう。
12cmの直線を書けばいいので、じょうぎで12cmの直線を引こう。
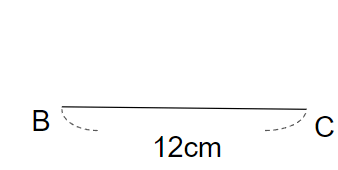
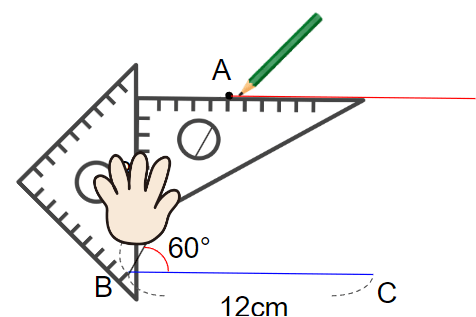
②角Bの角度をはかろう
つぎは辺ABを書きたいのだけれど、てきとうに書くわけにはいかないよね。
辺ABと辺BCの間の角は、大きさが60°と決まっているので、先に60°をはかるひつようがあるんだ。
分度器を角Bに当てて、60°のところに線を引こう。
このとき、線の長さは「とりあえずの長さ」で大丈夫。
辺ABが9cmなので、それよりも長くなるようによゆうをもって書いておこう。
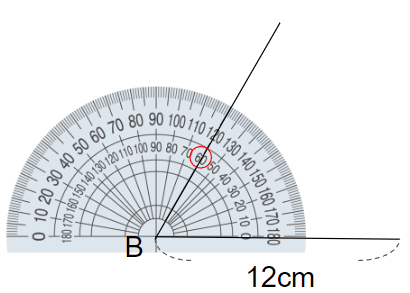
分度器を外すと次のようなところまで書けているはず。
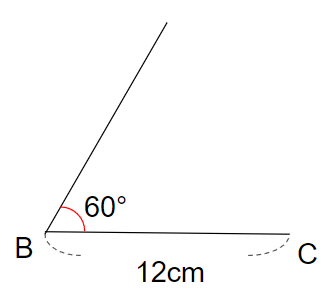
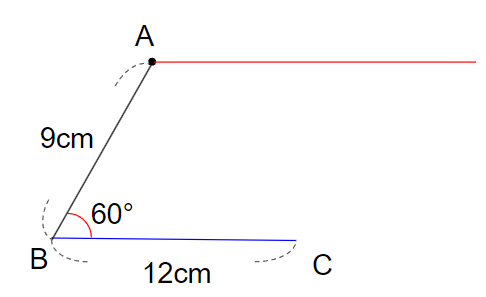
③辺ABの長さをはかろう
辺ABの長さは9cmだから、点Bからじょうぎではかって、9cmのところに印をつけよう。
その印の場所が、点Aになるよ。
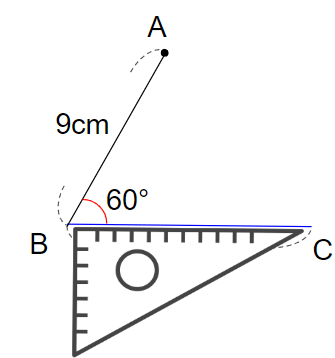
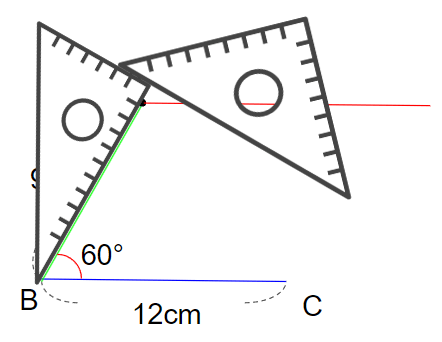
④辺BCに平行な直線を引こう
いよいよここで「平行な線の書き方」を使うよ。
次のようなじゅんばんで、「点Aを通る、辺BCに平行な直線」を引くよ。
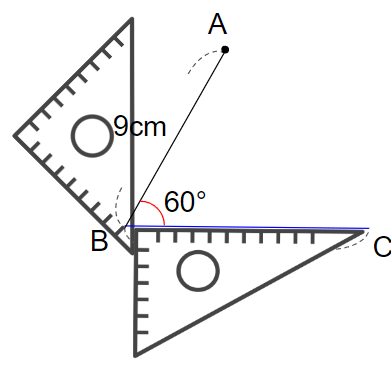
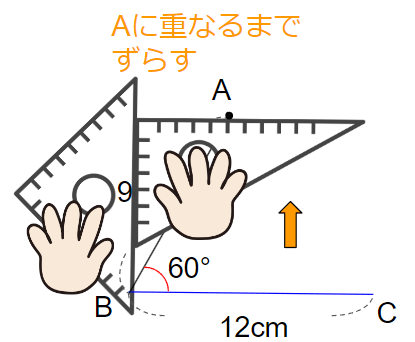
点Aに重なるまでずらせたら、点Aを通る直線を引こう。
ここでもできるだけ長めに線を書いておくといいよ。
ここまでできたら、1回じょうぎを外してみよう。
下のような図が書けているはずだよ。
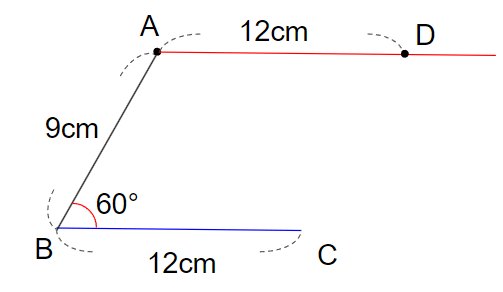
⑤辺ADの長さをはかろう
平行四辺形の向かい合った辺の長さは等しくなるから、辺BCが12cmならば、辺ADも12cmになるよね。
だから、点Aからじょうぎではかって、12cmのところに印をつけよう。
その印の場所が点Dだよ。
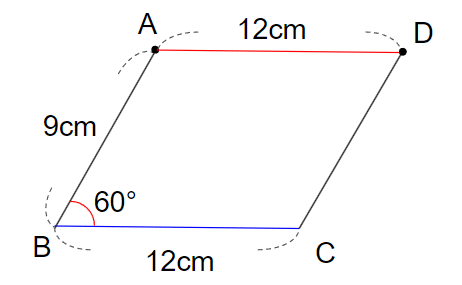
⑥点Cと点Dを結ぼう
点Cと点Dをじょうぎで結べたら、平行四辺形の完成だね。
平行四辺形の他の書き方
下のところまで書けたとしよう。

「平行な線の書き方」を使って、辺ABに平行な直線を書くやり方もあるんだ。
下のじゅんばんで書いていくよ。
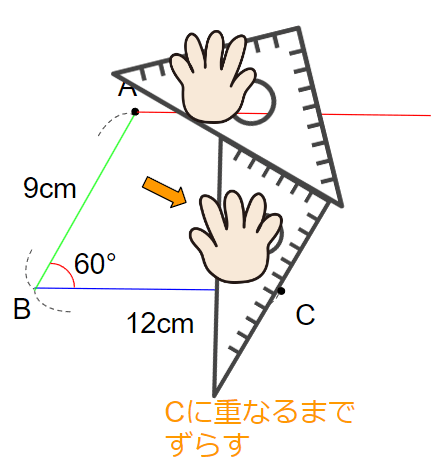
点Cに重なるまでずらせたら、点Cを通る直線を引こう。
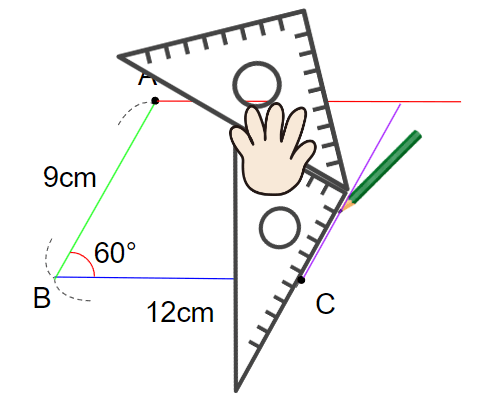
ここまでできたら、1回じょうぎを外してみよう。
平行四辺形が出来上がっているはずだよ。
自分が書きやすい書き方をマスターしておこうね。
「ひし形」とは
「ひし形(ひしがた)」っていうのは、「4つの辺の長さがすべて等しい四角形」のことだよ。
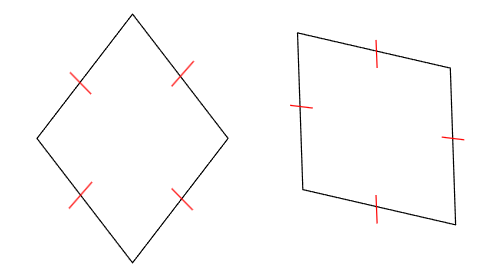
トランプのダイヤのような形がひし形だね。
ひし形の特徴
ひし形には次のような特ちょうがあるんだ。
ひし形の特ちょう
- 2組の向かい合った辺が平行になっている。
- 向かい合った角の大きさが等しい。
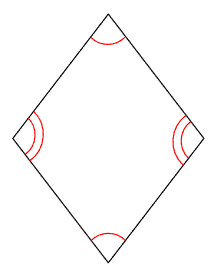
「向かい合った2組の辺がそれぞれ平行」ということは、ひし形も平行四辺形のなかまだね。
そう、ひし形も2組の辺が平行になっているから、「平行四辺形」ともいえるんだ。
下の図ようなイメージだね。
ひし形と長方形の違いは、ひし形は4辺の長さが同じだけれど、長方形は2組みの辺がそれぞれ同じで、4辺が同じではないよね。
長方形は4つの角がすべて直角だけれど、ひし形はそうではないよね。
ひし形と正方形の違いは、ひし形も正方形も4辺の長さが同じだけれど、正方形はさらに4つの角がすべて直角なのに対して、ひし形はそうではないよね。
平行四辺形と言ってもいろいろな形があることがわかるね。
「いろいろな四角形(台形・平行四辺形・ひし形)」まとめ
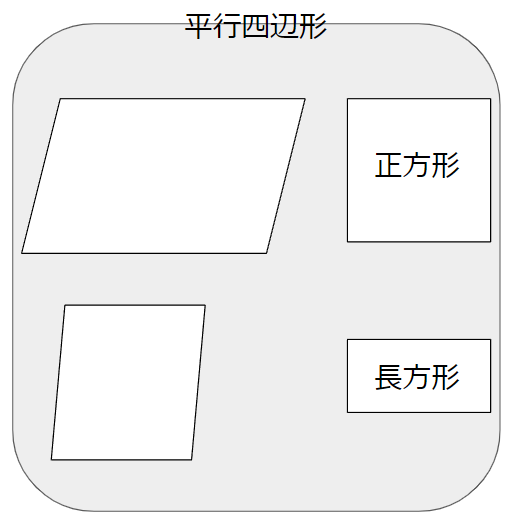
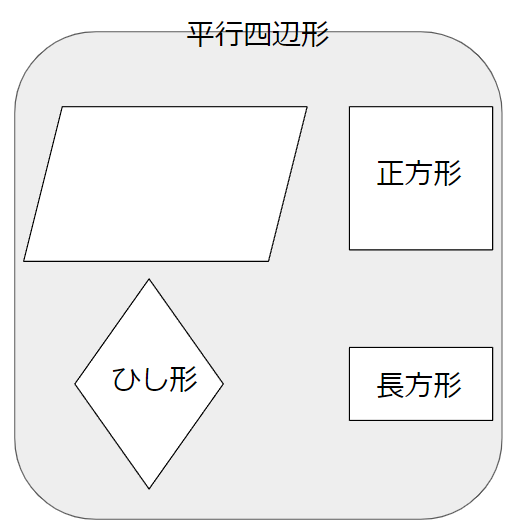
今回は四角形を「平行」に注目してわけたよ。
イメージは次のような感じ。
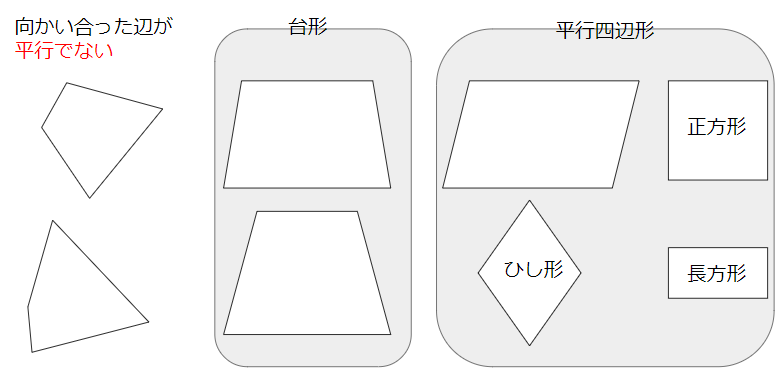
平行四辺形とは「2組の向かい合った辺が平行な四角形」のことだから、正方形や長方形、ひし形も平行四辺形のなかまになるんだったね。
いろいろな四角形の条件と特徴
それぞれの四角形になるための条件(どんなことがひつようか)と、どんな特ちょうがあるかを表にまとめたよ。
| 四角形 | 4つの辺が平行かどうか | 辺の長さ | 角の大きさ |
|---|---|---|---|
| 台形 | 1組の向かい合った辺が平行 | 同じではない ※平行ではない向かい合った辺の長さが同じばあいはある | 向かい合った角の大きさは同じではない ※となりどうしの角の大きさが同じばあいはある |
| 平行四辺形 | 2組の向かい合った辺が平行 | 2組の向かい合った辺の長さは同じ | 2組の向かい合った角の大きさが同じ |
| ひし形 | 2組の向かい合った辺が平行 | 4つの辺の長さがすべて同じ | 2組の向かい合った角の大きさが同じ |
| 長方形 | 2組の向かい合った辺が平行 | 2組の向かい合った辺の長さは同じ | 4つの角がすべて直角で同じ |
| 正方形 | 2組の向かい合った辺が平行 | 4つの辺の長さがすべて同じ | 4つの角がすべて直角で同じ |
「いろいろな四角形」まとめ
- 平行四辺形
・向かい合った2組の辺が平行な四角形
・向かい合った辺の長さが等しい
・向かい合った角の大きさが等しい - ひし形
・辺の長さがすべて等しい四角形
・向かい合った辺が平行
・向かい合った角の大きさが等しい - 台形
・向かい合った1組の辺が平行な四角形
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。




