「倍の見方と割合」倍と割合をわかりやすく解説(倍の見方の問題)
「倍の計算」とは(3年生のおさらい)
「倍」については3年生でも勉強したね。3年生と4年生のちがいをざっくりしょうかいすると、下の表のようになるよ。
| 3年生の内よう | 4年生の内よう |
| 2けた÷1けた 35まいは、5まいの何倍? | 3けた÷3けた 540まいは180まいの何倍? 2けた÷2けた 72まいは18まいの何倍? |
| 「割合」という言葉が登場する |
わり算の計算がめんどくさくなるのと、「割合」という言葉が登場するだけで、あとは3年生の勉強と変わらないと思っていたらOK。
だから、まずは3年生のおさらいをしていこう。
けんたさんは色紙を35枚持っています。
けんたさんの妹は、5枚持っています。
けんたさんは妹の何倍持っていますか
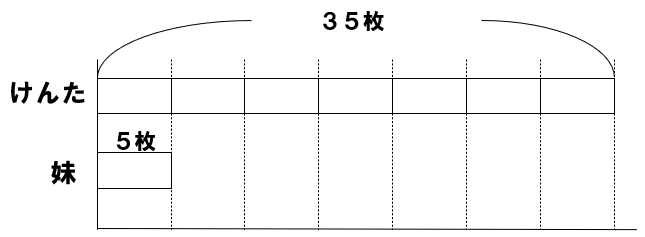
図で考えると
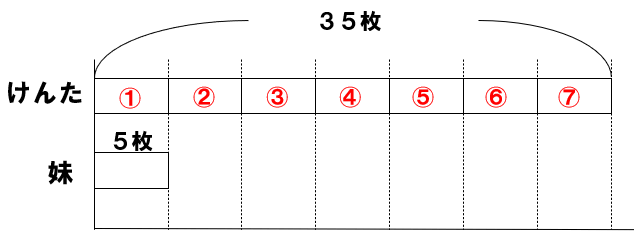
35枚は5枚の7こ分だとわかるよね。
つまり、7倍だよ。
式で考えると
「妹の色紙の枚数」を何倍かしたら、「けんたの色紙の枚数」
になるから、

▢を求めるためにはわり算を使ったらよかったよね。
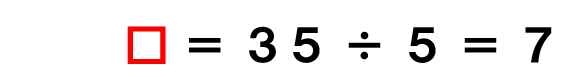
けんたさんは妹の7倍の色紙をもっていることになるよ。
「倍の見方」とは?倍をつかって比べてみよう
さっきの3年生のおさらいがわかったら、今回の内容もむずかしくないはず。
色紙の問題で、
妹の色紙の枚数5枚(もとにする大きさ)を1としよう。
そうすると、けんたさんの色紙の枚数35枚(くらべられる大きさ)は
7にあたるよね。
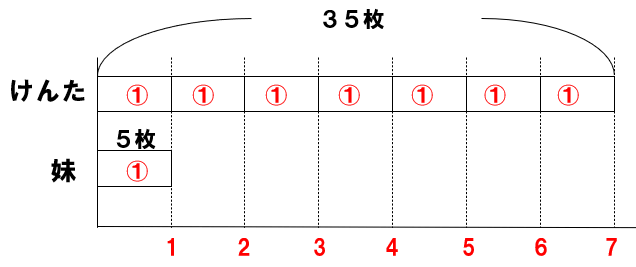
7倍っていうのは、5枚を1としたとき、35枚が7にあたるということを表しているんだ。
「なんだ。3年生の勉強とほとんど変わらないじゃん」と思ったよね。
「割合」とは
4年生ではじめて「割合」という言葉が登場するんだ。
「割合」っていうのは、
「もとにする大きさを1としたとき、くらべられる大きさがどれだけにあたるか」を表した数のことなんだ。
だから、さっきの問題でいったら、「7倍」が割合になるんだ。
割合の求め方は次の通り。
3年生で勉強した「何倍かを求める式」と同じになることをかくにんしよう。
割合の求め方
割合=くらべられる大きさ÷もとにする大きさ
他の問題でも「割合」を求めてみよう。
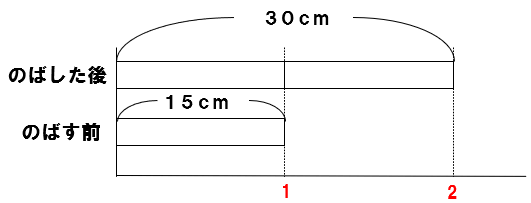
包帯Aは15cmで、のばすと30cmになります。
何倍になっていますか?
もとの長さは15cmで、のばすと30cmになるから、
もとの長さを1とすると、のばしたときの長さは2になるよね。
(割合=30÷15=2)
きちんと式をたてて計算すると次のようになるよ。

▢を求めるためにはわり算を使ったらよかったよね。
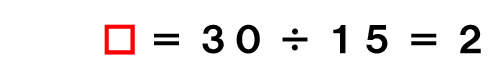
包帯Aをのばすと「2倍」になっていることがわかったね。
これが「割合」だよ。
割合を求めるよさ
割合を使えば
もとにする大きさがちがうときでも、2つの量をくらべることができるんだ。
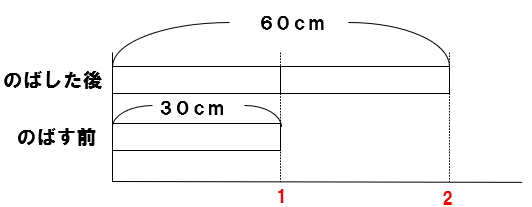
たとえば、下の包帯Aと包帯Bはどちらがよくのびるといえるかな?
| 包帯A | 包帯B | |
| のばす前 (もとにする大きさ) | 15cm | 15cm |
| のばした後 | 30cm | 45cm |
のばす前(もとにする大きさ)が同じだから、のばした後の長さが長い「包帯B」の方がよくのびると言えるよね。
じゃあ、下の包帯Bと包帯Cはどちらがよくのびるといえるかな?
| 包帯B | 包帯C | |
| のばす前 (もとにする大きさ) | 15cm | 30cm |
| のばした後 | 45cm | 60cm |
どちらとも、30cmのびているから、同じくらいのびるといえそうだよね。
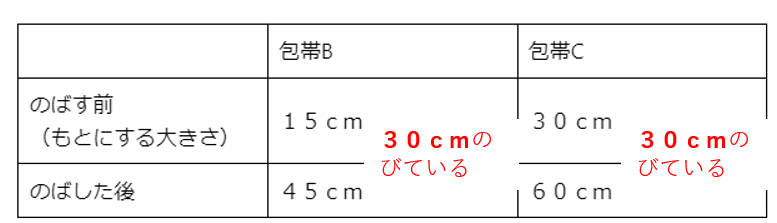
ただ、包帯Bと包帯Cではもとの長さがちがうよね。
こういう、もとの大きさがちがうときに、「割合」は役に立つんだ。
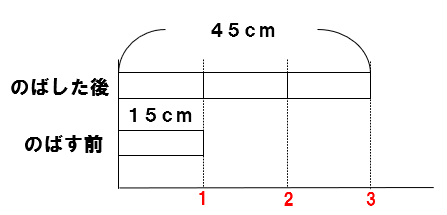
のばす前の長さを1として考えると、
包帯Bののびた割合は
「くらべられる大きさ」÷「もとにする大きさ」で求めることができるから、
45÷15=3倍
包帯Cののびた割合は
60÷30=2倍
まとめると次のようになるよ。
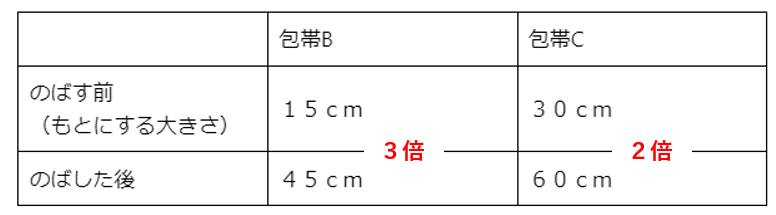
包帯Bの方がよくのびるといえそうだね。
割合を使えば
もとにする大きさがちがうときでも、2つの量をくらべることができるんだ。
「倍の見方」の練習問題
車の長さが3m、トラックの長さが15mでした。
トラックの長さは車の長さの何倍ですか。
車の長さ3m(もとにする大きさ)を1としよう。
そうすると、トラックの長さ(くらべられる大きさ)は
5にあたるよね。
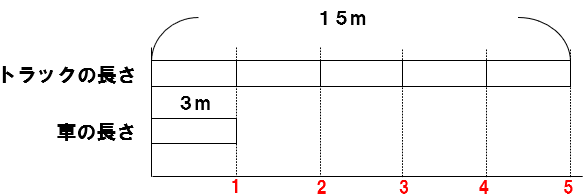
だから、トラックの長さは車の長さの5倍と求めることができるね。
次のように式で考えてもいいね。

▢を求めるためにはわり算を使ったらよかったよね。
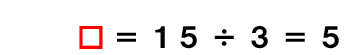
こどもの体重は24kgで、お父さんの体重はこどもの3倍でした。
お父さんの体重を求めなさい。
今までは何倍かを求める問題だったけど、この問題は今までとはちがうよ。
こどもの体重24kg(もとにする大きさ)を1としよう。
そうすると、お父さんの体重は、こどもの体重の3こ分だよね。
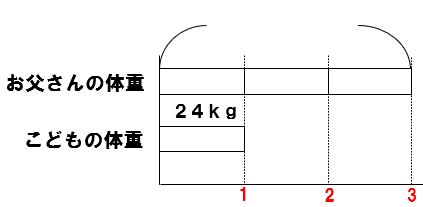
お父さんの体重は24kgの3こ分だから、
24×3=72kgと求めることができるね。
お父さんの身長はこどもの身長の3倍で180cmです。
こどもの身長を求めなさい。
こどもの身長(もとにする大きさ)を1としよう。
そうすると、お父さんの身長は、こどもの3こ分で180cmになるんだよね。
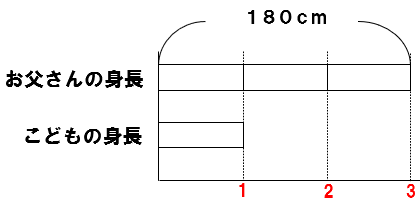
こどもの身長は1こ分だから
180÷3を計算したらいいね。
筆算で計算すると
180÷3=60となるよ。
(気になる人は筆算してみよう)
だから、こどもの身長は60cmと求めることができるんだ。
60cmってことは赤ちゃんかな。
「倍の見方と割合」のまとめ
「倍の見方と割合」のまとめ
- もとにする大きさを1としたとき、くらべられる大きさが何倍になっているかを考える。
- 割合とは
もとにする大きさを1としたとき、くらべられる大きさのこと - 割合は「くらべられる大きさ÷もとにする大きさ」ど求められる。
- 割合を使えば
もとにする大きさがちがうときでも、
2つの量をくらべることができる。
実は、「割合」は5年生や6年生でも登場するんだ。
4年生では「〇倍」の〇には、1、2、3・・・のような整数しか
入らないんだけど、5年生になると、〇に小数が入ったりしてくるよ。
なので、この4年生のうちに「割合」についてしっかり学習しておくと安心だよ!
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。



