計算のきまり「かっこのある計算の順序」のやり方と問題を解説
小学校4年生の算数で学習する「計算のきまり」のうち、「かっこ( )」がある計算の順序についてわかりやすく解説するよ。
かっこ( )のある計算・たし算・ひき算・かけ算・わり算は、どの順番で計算すればいいのか、その理由もあわせてくわしく紹介しているよ。
練習問題をときながら計算のきまりをマスターしよう!
目次
計算にはきまりがあって
きまりを知らないと、答えがちがってしまうんだ。
4年生では
たし算、ひき算、かけ算、わり算、かっこ( )がまじった式では、どういうじゅんじょで計算するかを勉強していくよ。
小学校だけではなくて、中学校や高校も大事になってくる内ようだから
まちがえなくなるまで何度も計算の練習をしていこう。
かっこ( )のある計算の順序
かっこのある計算には次のきまりがあるんだ。
かっこのある計算のじゅんじょ
- かっこ( )の中を先に計算する
どうして、かっこ( )の中を先に計算するのかというと、
ズバリ「この計算を先にしてあげてね!」ということを伝えるために( )を使うようになったから。
たとえば、スーパーでおかしを買うことを想像してみよう。
500円玉を持って、「120円のチョコと、80円のグミ」を買うとするよ。
レジでは、「120円のチョコと、80円のグミで、合わせて200円です。」と言われるよね。
そして、500円玉を渡すと、500円から、120円のチョコと80円のグミの合計200円を引いて、300円のおつりを返してくれるね。
この計算って、式に表すと
500-(120+80)になるんだよ。
言葉であらわすと、「500から、120と80を足したものを引く」ということだね。
もし、かっこ( )を使わなかったらどうなるかな?
500-120+80だと、答えは460になってしまうよね。
言葉であらわすと、「500から120を引いて、80を足す」になってしまうんだ。
これでは、おかしいよね。
なぜか、グミのぶんのお金の80円をもらえることになってしまうからね。
なので、かっこ( )がある問題は、かっこ( )を先に計算すると覚えておこう。
かっこ( )のある計算問題
500-(130+120)を計算しよう。
かっこがあるから、
かっこの中を先に計算すると、
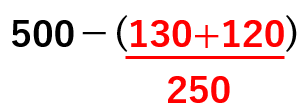
500-250=250になるよね。
500-(130×3)を計算しよう。
かっこの中を先に計算すると
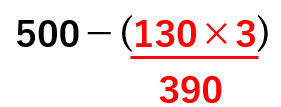
500-390=110になるね。
500-(120÷3)を計算しよう。
かっこの中を先に計算すると
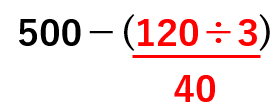
500-40=460になるね。
10×(17+3)を計算しよう。
かっこの中を先に計算すると
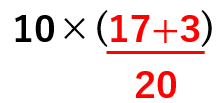
10×20=200になるね。
「なんだ。かんたんじゃん」と思ったよね。
かっこのある計算のじゅんじょをもう一度かくにんしよう。
かっこのある計算のじゅんじょ
- かっこ( )の中を先に計算する
次に「たし算、ひき算、かけ算、わり算」のじゅんじょを勉強していこう。
次からがレベルアップするからね。
たし算・ひき算・かけ算・わり算の計算の順序
小学校で出てくる問題で、一番先に計算しなくちゃいけないのは、かっこ( )の中なんだけど、次に計算するのは「×(かける)」と「÷(わる)」なんだ。
つまり、かけ算とわり算は、たし算とひき算よりも先に計算するんだよ。
計算のじゅんじょをまとめると次のようになるんだ。
下のじゅんじょはすごく大事だから覚えてしまおう。
計算のじゅんじょ(計算のきまり)
- かっこ( )の中
- 「×(かける)」「÷(わる)」
- 「+(たす)」「−(ひく)」
でも、「計算のきまりだから、かけ算とわり算は、たし算とひき算よりも先に計算するよ!」と、とつぜん言われても、
「・・・どうして?」とギモンに思うかもしれないね。
なぜ「かけ算とわり算」は「たし算とひき算」よりも先に計算するのか
かけ算は、そもそもどういうことを表しているのかを思い出してみよう。
「120円のチョコを5個買ったときの金がく」は、「120×5」という式で表すよね。
これって、「120を5回ぶん、たしている」ということなんだ。
つまり、「120+120+120+120+120」なんだよ。
でも、こんなにたくさん書くのは大変なので、「120×5」とべんりに表すことができるのが、「かけ算」なんだよね。
では、「100円のアメと、120円のチョコを5個買ったときの金がく」を式で表すとどうなるかな?
100+120×5
になるよね。
このとき、左からそのまま計算してしまったら、どうなるかな。
100+120=220、
220×5=1100
すごく高くなってしまったね。
本当なら、100円と、600円(120円×5個)の合計で、700円のはずだよね。
どうしてこうなってしまったかというと、左からじゅんばんに計算することで、たし算を先にしてしまうと、「220(100+120のこと)が5こ」の計算になってしまうからなんだ。
つまり、「220+220+220+220+220」になってしまうというわけ。
本当は、「100+120+120+120+120+120」だよね。
かけ算とわり算を、たし算とひき算よりも先に計算しないと、答えがまったくちがうものになってしまうんだね。
だから、「計算のじゅんじょのきまり」があるんだね。
もし、100円のアメと120円のチョコのセットを、5つ買ったときはどう表せばいいの?
この場合は、「100+120」のセットが5つということだよね。
なので、さっき学習した、かっこ( )を使って、
(100+120)×5
と表せばいいんだよ。
そうすれば、かけ算があっても、「先にたし算をするんだな」と伝わるからね。
計算の順序の問題
10+17×2を計算しよう。
計算はふつうは左から順に計算していくんだけど、
この問題は「+(たす)」「×(かける)」があるよね。
計算のじゅんじょでは、「×(かける)」の方が「+(たす)」より先だから、
次のようになるよ。
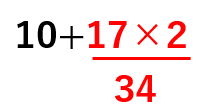
10+34=44になるよね。
10+17を先に計算して27。27に2をかけて54という風にまちがえないようにしよう。
5×2+4÷2を計算しよう。
計算はふつうは左から順に計算していくんだけど、
「×(かける)」「+(たす)」「÷(わる)」があるよね。
計算のじゅんじょでは、「×(かける)」「÷(わる)」の方が「+(たす)」より先だから、
次のようになるよ。
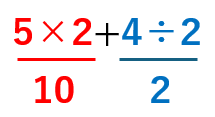
10+2=12になるよね。
計算のじゅんじょを知らないと
次のように計算してしまいそうだよね。
(まちがい)
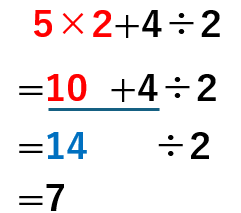
ぜんぜんちがう答えになっちゃうよね。
7×(8-6÷2)を計算しよう。
計算はふつうは左から順に計算していくんだけど、
「×(かける)」「−(ひく)」「÷(わる)」「かっこ( )」があるよね。
計算のじゅんじょをもう一度かくにんすると
①かっこ( )の中
②「×(かける)」「÷(わる)」
③「+(たす)」「−(ひく)」
だから、まずは
①かっこ( )の中を計算する
7×(8-6÷2)のかっこ( )の中には
「−(ひく)」と「÷(わる)」があるよね。
「÷(わる)」の方が「−(ひく)」より先に計算するから
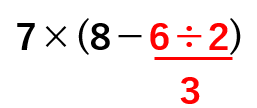
8-3を計算すると、
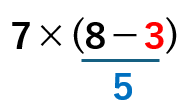
かっこ( )の中を計算することができたね。
②×(かける)
かっこ( )の中は「5」になるから、
7×5=35になるよね。
4×(8+2-3)÷2を計算しよう。
計算はふつうは左から順に計算していくんだけど、
「×(かける)」「+(たす)」「−(ひく)」「÷(わる)」「かっこ( )」のすべてがあるよね。
計算のじゅんじょをもう一度かくにんすると
①かっこ( )の中
②「×(かける)」「÷(わる)」
③「+(たす)」「−(ひく)」
だから、まずは
①かっこ( )の中を計算する
4×(8+2-3)÷2のかっこ( )の中は
「+(たす)」「−(ひく)」だけだから、
ふつうに左から順に計算していこう。
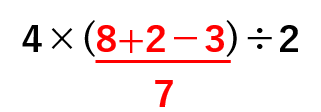
②「×(かける)」
かっこ( )の計算が終わると
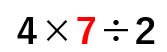
「×(かける)」と「÷(わる)」だけだから
ふつうに左から順に計算していこう。
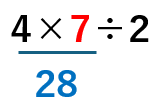
③「÷(わる)」
28÷2=14と求めることができたね。
(8-2×3)+6÷2を計算しよう。
計算はふつうは左から順に計算していくんだけど、
「×(かける)」「+(たす)」「−(ひく)」「÷(わる)」「かっこ( )」のすべてがあるよね。
計算のじゅんじょをもう一度かくにんすると
①かっこ( )の中
②「×(かける)」「÷(わる)」
③「+(たす)」「−(ひく)」
だから、まずは
①かっこ( )の中を計算する
(8-2×3)+6÷2のかっこ( )の中は
「−(ひく)」と「×(かける)」があるよね。
「×(かける)」の方が「−(ひく)」より先に計算するから
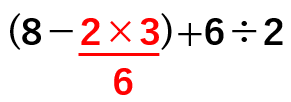
8-6を計算すると
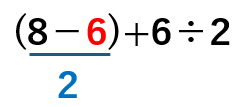
かっこ( )の中を計算することができたね。
②「÷(わる)」
かっこ( )の計算が終わると
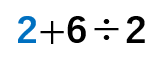
「÷(わる)」の方が「+(たす)」より先に計算するから
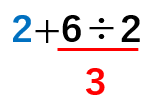
③「+(たす)」
2+3=5と求めることができたね。
計算のきまりの文章問題
計算のきまりを使った文章問題を見ていこう。
1まい50円の紙を4まい買って、500円出しました。
おつりは何円ですか。
50円の紙を4まい買うと
50×4になるよね。
500円出したときのおつりを求めたいから
次のような式になるよ。
500-(50×4)
かっこ( )の中を先に計算しなくちゃいけなかったから
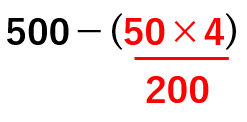
500-200=300円と求めることができるね。
1本100円のえんぴつ3本と、1こ50円の消しゴム4こを買ったときの合計の金がくを答えなさい。
100円が3本だから、100×3 円
50円が4こだから、 50×4 円
合計の金がくだから
2つの金がくを足せばOK。
100×3+50×4
「×(かける)」を先に計算するから
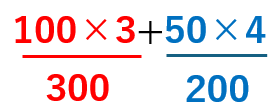
300+200=500円と求めることができるよ。
計算のきまり「かっこのある計算の順序」のまとめ
計算のじゅんじょは次の通りになる
- かっこ( )の中
- 「×(かける)」「÷(わる)」
- 「+(たす)」「−(ひく)」
小学校だけではなくて、中学校や高校も大事になってくる内ようだから
まちがえなくなるまで何度も計算の練習をしていこう。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。




