つるかめ算とは?面積図での解き方・応用練習問題をくわしく解説
「つるかめ算」とはなにか?面積図とはどういうことか?
つるかめ算の基本的なときかた、つるかめ算を面積図を使ってとく方法、中学受験でも出てくる「速さのつるかめ算」「売買損益のつるかめ算」「仕事算のつるかめ算」「弁償算のつるかめ算」のときかたをそれぞれくわしく解説するよ。
中学で学習する「方程式」とつるかめ算の関係、中学受験でつるかめ算をとく時に、方程式を使ってよいのかどうかについても紹介しているよ。
つるかめ算とは
「つるかめ算」だなんて聞くと、なんだか難しそう・・と思ってしまうかもしれないね。
でも、つるかめ算は、ややこしい文章題を解くために使えるとってもベンリなツール(問題を解く方法)なんだよ。
学校にもよるけれど、小学校4年生~5年生の算数で学習することが多いよ。
つるかめ算とは
文章題の解き方のひとつで、足が2本である「つる」と、足が4本である「かめ」の合計頭数(全部で何匹いるのか)と足の数の合計から、「つる」と「かめ」それぞれが何匹いるのかを求める問題のこと。
説明だけだと、いまひとつピンとこないよね。
例題をもとにくわしく説明するよ。
※「つる」はほんとうは「何羽」と数えるけれど、分けて書くとふくざつになってしまうので、ここでは「つる」も「かめ」も「何匹」と数えるよ。
つるかめ算の例題
「つる」と「かめ」が合わせて11匹います。
「つる」と「かめ」の足の数を合わせると、28本でした。
「つる」と「かめ」はそれぞれ何匹(何羽)いますか。
※「つる」の足は2本、「かめ」の足は4本であることをもとにかんがえましょう。
どうかな?
問題を読んだだけだと、なんだかとても難しそうだよね。
「つる」と「かめ」がそれぞれ何匹かだなんて、どうやってもわかりそうにない気がしてしまうよね。
だけれど、「つるかめ算」を使うと、こんな問題がかんたんに解けてしまうんだ。
「つるかめ算」の解き方
まず、「つる」と「かめ」がそれぞれ何匹いるのかはさっぱりわからないよね。
なので、「とりあえず、ぜんぶ『つる』だったらどうだろう」と考えてみるんだ。
もちろんぜんぶが「つる」ということは問題としてもありえないので、ぜんぶが「つる」として計算すると、「ズレ」がでてしまうよ。
この「ズレ」をなくすにはどうすればいいかを考えてあげれば、「かめ」が何匹なのかがわかるようになるんだ。
このように、
「まずはぜんぶが〇〇とする」→「ズレがでる」→「ズレがなくなるようにする」
この3ステップが、「つるかめ算」のポイントだよ。
では、じっさいにやってみよう。
➀ぜんぶを〇〇とする
問題のはじめの方をもういちどかくにんするよ。
「つる」と「かめ」が合わせて11匹います。
「つる」と「かめ」の足の数を合わせると、28本でした。
「つる」と「かめ」が合わせて11匹となっているけれど、ひとまず、ぜんぶが「つる」とするよ。
つまり、「つる」が11匹だと考えるんだ。
そうすると、つるの足の数は2本なので、
合計の足の数は2×11=22本だね。
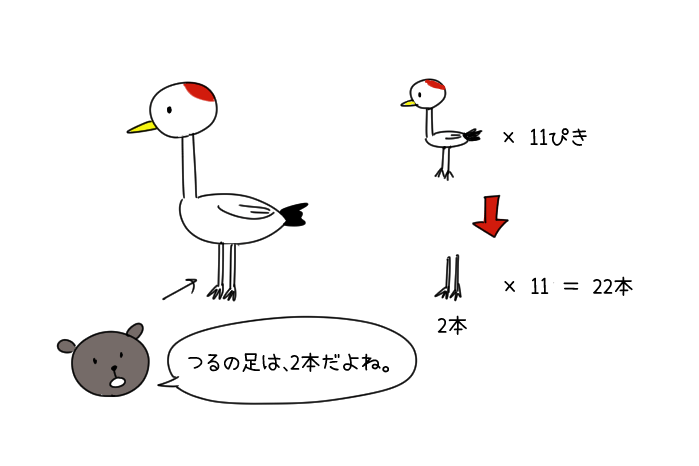
でも、問題では「足の数を合わせると、28本でした。」と書いてあるよね。
そう、この「22本」と「28本」が「ズレ」なんだ。
➁ズレがなくなるように考えよう
ほんとうなら「28本」なのに、「22本」になってしまったということは、「6本」足りないということだよね。
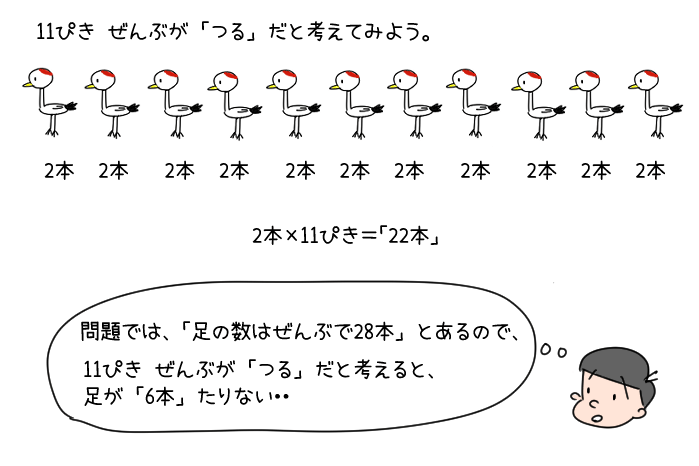
どうしたらこの「6本」がちょうどよくおさまるかを考えるのだけれど、ここが少しむずかしいので、じっくり説明するよ。
1匹が交代するごとに、合計の足の数がいくつかわるか?をもとめる
まず、ぜんぶが「つる」ではないということだから、「つる」と「かめ」が何匹か交代しなくてはいけないよね。
たとえば、1匹の「つる」と「かめ」が交代したとするよ。
足の数は、どう変わるかな?

そう、1匹の「つる」と「かめ」が交代すると、合計の足の数は「2本」多くなるね。
「ズレ」をなくすには、何匹交代すればいいかをもとめる
今回のズレは、「6本足りない」だったよね。
ということは、1匹の「つる」と「かめ」が交代すると、合計の足の数は「2本」多くなるのだから、
6÷2=3
そう、3匹の「つる」と「かめ」が交代すればいいことがわかるんだ。
③さいしゅうてきな「つる」と「かめ」の数をもとめる
さいしょ、「つる」を「11匹」として考えたよね。
そこから、3匹の「つる」と「かめ」が交代するのだから、
つるは 11-3=8
かめは 0+3=3
というわけで、「つる」は8匹、「かめ」は3匹ともとめることができたよ。
つるかめ算の解き方3ステップ
➀ぜんぶを○○とする
→11匹ぜんぶ「つる」なら、足の数は22本。
ズレは、28本-22本で「6本足りない」。
➁ズレがなくなるように考える
→「つる」と「かめ」が1匹交代すると、足の数は「2本増える」。
3匹交代すれば、2×3=6で「6本増える」(ズレがなくなる)。
③それぞれ何匹になるのか計算する
→11匹から3匹交代するから、
「つる」は11-3=8匹
「かめ」は0+3=3匹。
つるかめ算は、どのような問題で使えるのか?
とってもべんりな「つるかめ算」だけれど、どんな問題のときに「つるかめ算」が使えるのかを見分けることができるかもポイントなんだ。
テストはもちろん、中学受験などでも、ふくざつな文章問題が出てきた時に、「これは、つるかめ算を使えば解けるぞ!」と気がつくことができるかどうかでぜんぜんちがうからね。
「つるかめ算」を使うことができるかどうかの見分けポイントを紹介するよ。
つるかめ算が使える問題の条件2つ
- それぞれの「1つあたりの量」がわかっているか。
- 2つ以上の「全体の数」がわかっているか。
それぞれの「1つあたりの量」とは
例題では、「つる」の足は2本、「かめ」の足は4本とわかっていたよね。
つまり、それぞれ(つるとかめ)の1つあたりの量(足の数)がわかっているということだよ。
「1つあたりの量」には、ほかにもこんなものがあるよ。
- 1袋に入っている、アメの数
- 1日にできるドリルのページ数
- アメ1つあたりの金額
2つ以上の「全体の数」とは
例題では、「つるとかめの足の数の合計は28本」と、「つるとかめは合わせて11匹」ということがわかっていたよね。
全体の数には、こんなものがあるよ。
- ぜんぶのお菓子の数
- ぜんぶでできたドリルのページ数
- ぜんぶを買ったときの金額
問題文のなかに、それぞれ「○○の数は△△」ということばと、「ぜんぶで××」ということばがセットで出てきたら、「これはつるかめ算かも!」と考えてみよう。
「つるかめ算」の基本問題を紹介するので、文章問題から「つるかめ算かどうか」を見分ける練習をしよう。
「つるかめ算」の基本問題
太郎くんはスーパーでチョコレートとアメを合わせて8つ買いました。
合計の金額は330円でした。
チョコレートは1つ60円、アメは1つ30円のとき、チョコレートとアメをそれぞれいくつ買ったかもとめましょう。
「つるかめ算」かどうか見分けよう
つるかめ算を使えるかどうかの条件は2つだったね。
- それぞれの「1つあたりの量」がわかっているか。
- 2つ以上の全体の数がわかっているか。
それぞれの「1つあたりの量」は、「チョコレートは1つ60円」、「アメは1つ30円」ということがわかっているので、クリアだよ。
2つ以上の「全体の数」は、「合計の金額が330円」ということと、「合わせて8つ買った」ということがわかっているので、これもクリアだね。
「つるかめ算」が使えることがわかったので、たとえば「すべてチョコレートだったとしたら」を考えるよ。
➀ぜんぶを○○とする
→8個ぜんぶチョコレートだったとしたら、合計金額は480円。
ズレは、330円-480本円で「150円多い」。
➁ズレがなくなるように考える
→「60円のチョコレート」と「30円のアメ」が1つ交代すると、金額は「30円少なくなる」。
5個交代すれば、30×5=150で「150円少なくなる」(ズレがなくなる)。
③それぞれ何匹になるのか計算する
→8個から5個交代するから、
「チョコレート」は8-5=3個
「アメ」は0+5=5個。
太郎くんとももこさんは、交代でおりがみで鶴を作ることにしました。太郎くんは1日に13羽の鶴を作ることができます。ももこさんは、1日に17羽の鶴をつくることができます。
2人合わせて、7日間で103羽の鶴を作りました。
太郎さんと、ももこさんが鶴を作ったのはそれぞれ何日ですか。
それぞれの「1つあたりの量」は、「太郎くんは1日に13羽」、「ももこさんは1日に17羽」ということがわかっているので、クリアだよ。
2つ以上の「全体の数」は、「合わせて7日間」ということと、「合わせて103羽」ということがわかっているので、これもクリアだね。
➀ぜんぶを○○とする
→7日間ぜんぶ太郎くんが作ったとしたら、できあがる鶴の数は91羽。
ズレは、103羽-91羽で「12羽少ない」。
➁ズレがなくなるように考える
→「太郎くん(13羽)」と「ももこさん(17羽)」が1日ぶん交代すると、できあがる鶴の数は「4羽多くなる」。
3日ぶん交代すれば、3×4=12で「12羽多くなる」(ズレがなくなる)。
③それぞれ何匹になるのか計算する
→7日から3日ぶん交代するから、
「太郎くん」は7-3=4日
「ももこさん」は0+3=3日。
つるかめ算を面積図を使ってとく方法
つるかめ算は「面積図」を使ってとくこともできるよ。
「面積図を使ってとく」とは
長方形の面積の求め方は「縦×横」だよね。
なので「A x B = C」という式が登場する問題を、「縦=A、横=B、面積=C」というように図形におきかえて考える方法のことだよ。
図で考えることができるから、文章や式だけよりもわかりやすいのがメリットだよ。
たとえば、最初に紹介した「つる」と「かめ」の問題をもういちど面積図を使ってといてみよう。
「つる」と「かめ」が合わせて11匹います。
「つる」と「かめ」の足の数を合わせると、28本でした。
「つる」と「かめ」はそれぞれ何匹(何羽)いますか。
面積図を使ってとくには、「どうやって図形であらわすか」がいちばんのポイント。
問題にでてくる「動物」や「商品」をAとBとするよ。
キホンは、
・縦はAとBそれぞれの「1つあたりの量」
・横は「A+B」
・面積を「全体の数」
にするんだ。
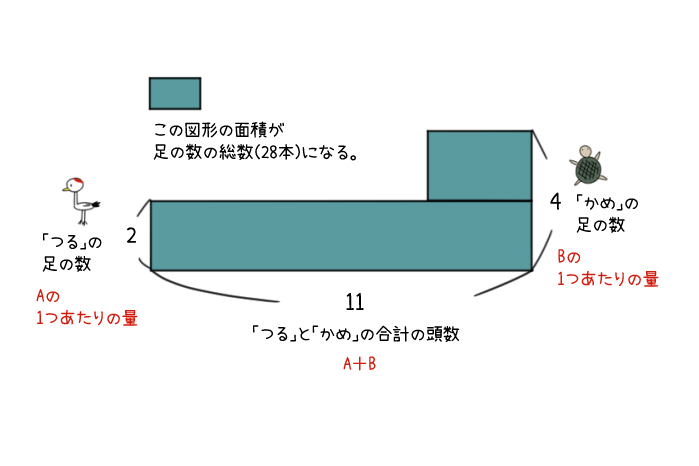
つるかめ算の面積図の書き方
1:AとB(今回なら、つる+かめ)の合計の数を横にとる。

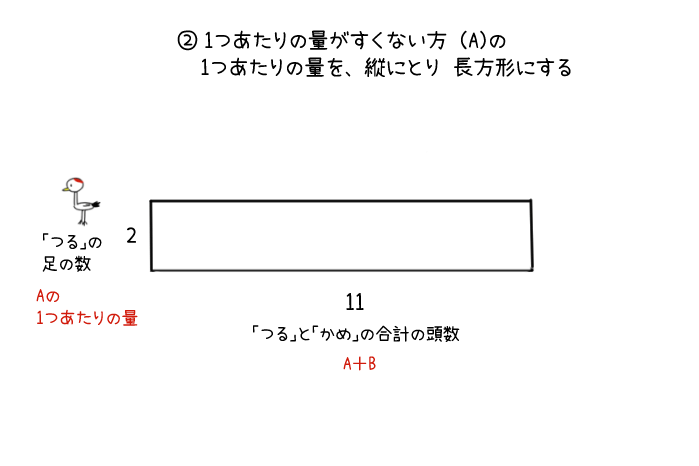
2:1つあたりの量がすくないほうの、1つあたりの量を縦にとって、長方形を作る(今回なら、つるのほうが足の数が少ないので、つるの足の数「2」を縦にとって長方形を作る)。
3:もうひとつのほう(かめ)の、1つあたりの量を反対の縦にとって、長方形を上にかさねるように作る。
このとき、横はばは今はわからないので、めやすでOK。
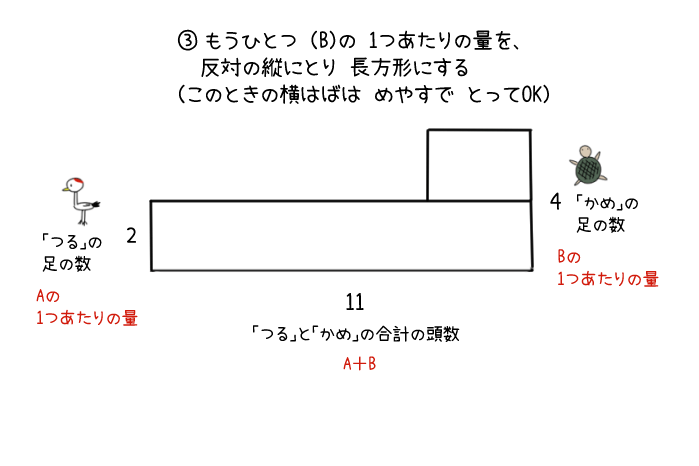
このとき、上にできる長方形の縦は、「かめ」の足の数から「つる」の足の数を引いた「2」になるよ。
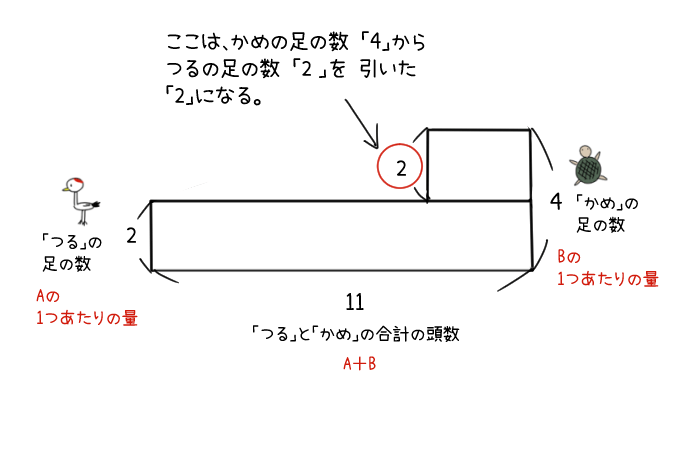
こうやって面積図が書けたら、こんどは面積図からどうやって答えを導き出すのか説明するよ。
つるかめ算の面積図 答えの求め方
まずは面先図のそれぞれの長方形の面積を求めるよ。
下にある長方形をAとして、上にのっている長方形をBとするよ。
Aの面積は、縦も横もわかっているから、計算することができるね。
2×11=22だね。
Bの面積は、縦はわかっているけれど、横がまだわからないね。
横を「△」とすると、式は
2×△
になるね。
そして、AとBの面積を足すと、合計の足の数である「28」になるんだ。
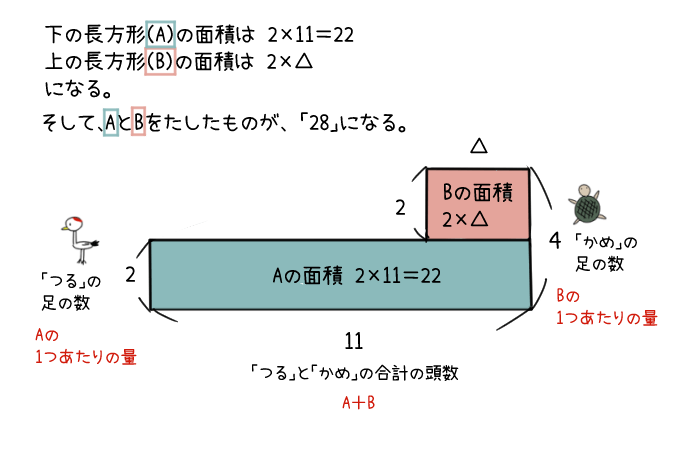
ということは、28からAの面積である22を引くと、Bの面積がわかるね。
28-22=6
Bの面積は、「6」になるはずだね。
なので、2×△=6
△=3
とわかるよ。
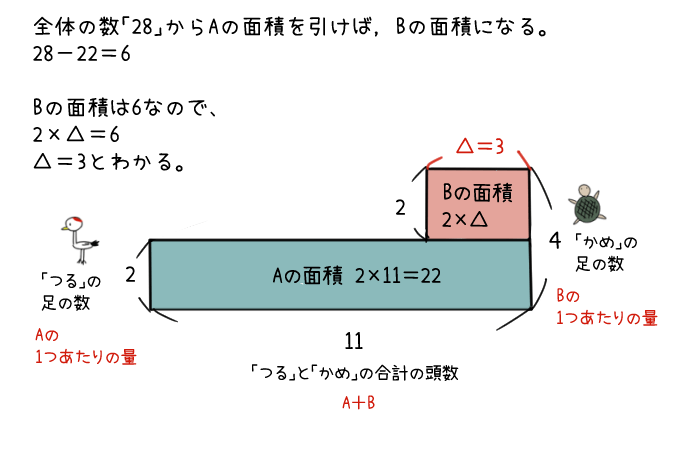
△の数がわかったので、上の長方形と下の長方形の横の差(✩とするよ)も求めることができるね。
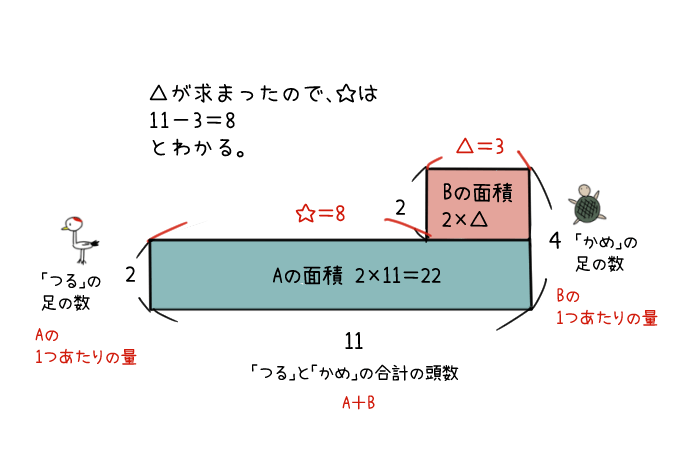
11-3=8
これで、「つる」の数と「かめ」の数がわかったね。
答え:つるが8ぴき、かめが3びき
「つる」と「かめ」の数がハッキリしたところで、あらためて図で表すとこうなるよ。
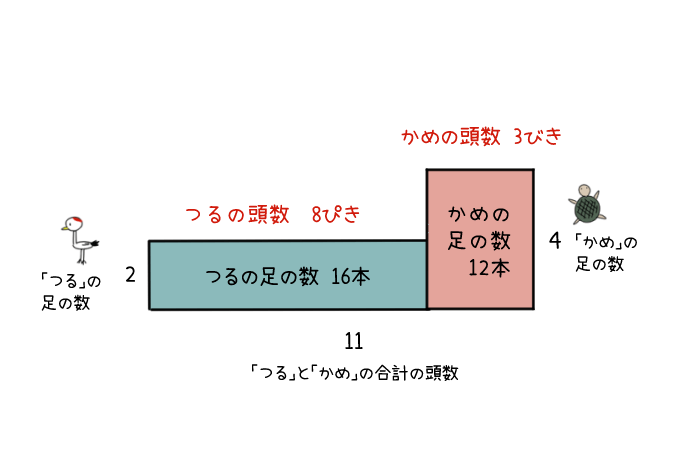
さいしょに下の長方形を横はばぜんぶを使って書くのは、「とりあえずぜんぶをつるとして考える」ことと同じだったんだね。
つるかめ算で面積図を使うメリット
つるかめ算には、面積図を使わないとうまくとけない問題もあるんだ。
それは、動物や商品などが3種類以上でてくるとき。
今回は「つる」と「かめ」の2種類だったけれど、もしここに8本足の「たこ」も出てきたら、面積図を使う必要がでてくるよ。
つるかめ算の応用問題「速さのつるかめ算」
ふくざつな文章問題になると、その問題が「つるかめ算かどうか」がわからなくて、こまってしまうケースが多いよ。
いろいろなタイプのつるかめ算の応用問題を紹介するので、できるだけ慣れておこう。
算数で「速さの問題」といえば、「時間・道のり・速さ」が出てくる問題だね。
その中でも、「全体の道のりと時間が分かっていて、途中で速さが変わる」問題の場合、つるかめ算でとくことができるよ。
「速さのつるかめ算」と呼ばれているんだ。
たろう君が3.6kmはなれた友達の家にあそびに行きました。しばらく分速40mで歩いていましたが、途中で自転車をかりて、分速300mで走ったところ、25分でとうちゃくしました。
たろう君が歩いていた時間をもとめましょう。
わかっていることは、
- 全体の道のり=3.6km
- 速さ➀=分速40m
- 速さ➁=分速300m
- 全体の時間=25分
だね。
「つるかめ算が使える問題の条件」をもういちどたしかめてみよう。
つるかめ算が使える問題の条件2つ
- それぞれの「1つあたりの量」がわかっているか。
- 2つ以上の「全体の数」がわかっているか。
今回の問題では、2つ以上の全体の数(全体の道のり・全体の時間)と、それぞれ1つあたりの量(速さ➀・速さ➁)がわかっているね。
だから、つるかめ算が使えるよ。
つるかめ算でのときかたのポイントは、「とりあえずぜんぶを、かたほうにする」だったよね。
なので、「ぜんぶ歩いた場合」を考えてみよう。
ぜんぶ歩いた場合、分速40mで25分歩いたら、
40×25=1000
1000m進むことができるね。
全体の道のりは3.6km(3600m)なので、
3600-1000=2600
ズレは、2600mだね。
それでは、歩いたときと、自転車の時を交代すると、1分あたり
300-40=260
260mのズレがなくなるね。
2600mのズレをなくすには、
2600÷260=10
10分、歩きと自転車の時間を交代すればいいね。
10分交代するから、
「歩き」は25-10=15分
「自転車」は0+10=10分。
つるかめ算の応用問題「売買損益のつるかめ算」
「売買損益(ばいばいそんえき)」とは、品物を売ったり買ったりしたとき、その売りあげや、どのくらい損をしたかを計算することだよ。
ぜんたいの売りあげの金額や、ぜんぶの売れた数がわかっていて、とちゅうで品物をうるねだんが変わったりするばあい、つるかめ算が使えるよ。
「速さがとちゅうでかわる問題」とおなじ考えかたになるんだ。
くだもの屋さんは、1個50円で仕入れたりんごに、3割の利益(りえき)になるようにねだんをつけて、90個売ることにしました。
1日目にいくつか売れて、2日目には2割引で売ったところ、すべて売り切れました。2日間の売りあげの合計は、6300円でした。
1日目に売れたりんごの数をもとめましょう。
「3割」「2割引」ということばが出てくるように、この問題は5年生で学習する「割合」の考えかたがひつようになるよ。
2つの全体の数は、「90個」と「6300円」でわかっているね。
それぞれの1つあたりの量を、割合をもとにもとめなくてはいけないよ。
1日目のりんごのねだん=50+(50×0.5)=75円
2日目のりんごのねだん=75-(75×0.2)=60円
2つの全体の数と、それぞれの1つあたりの量がわかったので、つるかめ算が使えるね。
すべて60円で90個を売ったとするよ。
60×90=5400
ズレは、
6300-5400=900円。
1日目のりんごのねだんと、2日目のりんごのねだんを交代すると、1つあたり
70-60=15
15円のズレがなくなるね。
900円のズレをなくすには、
900÷15=60
60個、1日目のりんごと2日目のりんごの数を交代すればいいね。
1日目に売れたりんごの数=0+60=60個
2日目に売れたりんごの数=90-60=30個。
つるかめ算の応用問題「仕事算のつるかめ算」
「仕事算」とは、人によってできる仕事の量がきまっていて、「ぜんぶの仕事を終わらせるにはどのくらいかかるか」とか、「○○が仕事をしたのはどのくらいか」ということをもとめる問題だよ。
ポイントは、「ひとりあたりができる仕事の量」を考えること。
ただ、ひとりあたりができる仕事の量をもとめるには、小学校5年生で学習する「最小公倍数」ができるようになっていなくてはいけないよ。
そんな仕事算のうち、つるかめ算でとける問題をしょうかいするよ。
発表会のじゅんびを、たろう君とももこさんでします。
たろう君が1人ですると25時間、たろう君とももこさん2人ですると15時間かかる仕事があります。
たろう君が何時間かこの仕事を1人でしたあとに、ももこさんに交代したところ、ぜんぶで30時間かかりました。
たろう君が1人で仕事をした時間をもとめましょう。
仕事算は、まず「ひとりあたりができる仕事の量」を考えるひつようがあったね。
そのために、全体の仕事量をもとめるよ。
全体の仕事量は、「25時間」と「15時間」の最小公倍数で考えるんだ。
わからなかったら読もう!
「なぜ仕事算の全体の仕事量は最小公倍数になるのか?」
じつは、仕事算の「全体の仕事量」は、「たとえば全体の仕事量が○○だとしたら」と、問題をとく人が仮に自由に決めてしまっていいんだ。
仕事算で大切なのは、「それぞれができる仕事量」だからね。
たとえば、全体の仕事量を仮に「250」にすれば、たろう君はそれに25時間かかるので、1時間あたり「10」の仕事ができることになるね。
でも、2人で仕事をしたばあいは15時間かかるので、1時間あたり16.6666・・・と割り切れなくなってしまう。
そうならないために、「25」と「15」、両方で割り切ることができる、いちばん小さい数(最小公倍数)をもとめるんだよ。
25と15の最小公倍数は75だね。
これなら、
たろう君が1時間あたりでできる仕事量=75÷25=3
2人で1時間あたりできる仕事量=75÷15=5
となって、計算がかんたんになるからね。
25と15の最小公倍数は75だね。
たろう君が1時間あたりでできる仕事量=75÷25=3
2人で1時間あたりできる仕事量=75÷15=5
たろう君が1時間あたりでできる仕事量が3なのだから、ももこさんが1時間あたりでできる仕事量=5-2=2だね。
これで、2つの全体の量(全体の時間30時間・全体の仕事量75)と、それぞれ1つあたりの量(たろうは3、ももこは2)がわかったね。
なので、つるかめ算が使えるよ。
すべてももこさんが仕事をしたとすると、
2×30=60
ズレは、
75-60=15
ももこさんとたろう君を交換すると、1時間あたり
3-2=1の仕事量がかわる。
ズレをなくすには、
15÷1=15
ももこさんが仕事をした時間は30-15=15時間
たろう君が仕事をした時間は0+15=15時間。
つるかめ算の応用問題「弁償算のつるかめ算(面積図でのとき方)」
太郎くんとももこさんで、すごろくをします。
ジャンケンに勝つと、3マスすすめます。ジャンケンに負けると、2マスもどります。
ジャンケンを7回したところ、太郎くんは1マス進むことができました。
太郎くんは何回勝ち、何回負けましたか。
ただし、あいこは無かったとします。
この問題では、ジャンケンに勝つと3マスすすめるけれど、負けると2マス戻らなくてはいけないよね。
ほかにも「お皿を1まい運ぶと200円もらえるけれど、割ってしまうと100円払わなければならない」など、「あることをするとプラスだけれど、あることをするとマイナスになる」ような問題を「弁償算」と呼ぶよ。
弁償算はマイナスがあるので、面積図で考えるときにはちょっとコツがひつようなんだ。
マイナスを図であらわすために、基本のつるかめ算では上にのせた長方形を、下にくっつけるよ。
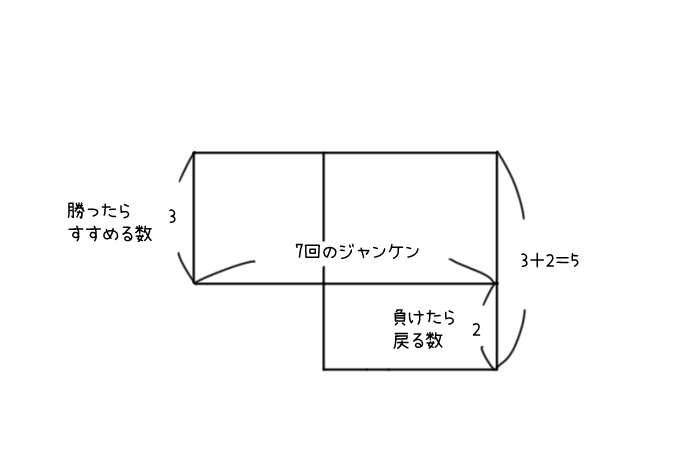
横はばは、基本のつるかめ算のときとおなじように、勝った数+負けた数の合計回数「7」にするよ。
縦は、プラスになる数である「勝ったらすすめる数」の「3」をとるよ。
もう片方は「負けたら戻る数」なので、マイナスをあらわすために、下向きに「2」をとるんだ。
このとき、下につける長方形の横はばは、やっぱり今はわからないので、めやすでOKだよ。
そうすると、右がわの縦の長さは、「勝ったらすすめる数の3」と「負けたら戻る数2」を足した「5」になるよね。
こうやって描けた図形のうち、かこまれている部屋をそれぞれ「A」「B」「C」とするよ。
このとき、AとBとCの関係をあらわすと、つぎのようになるんだ。
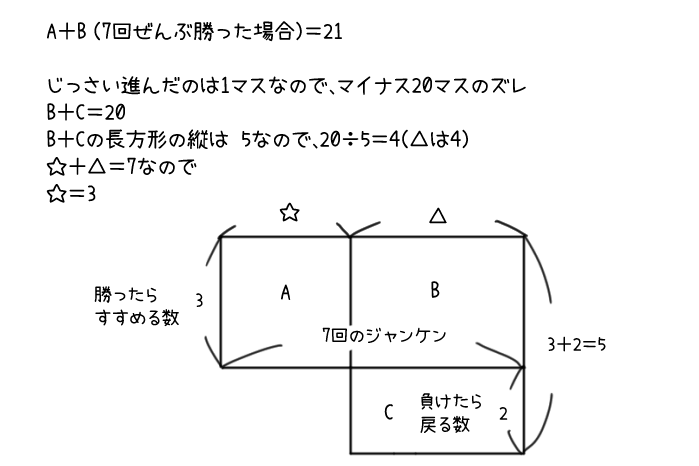
AとBをたした長方形は、横7×縦3、つまり「7回ぜんぶ勝ったばあいにすすめる数」をあらわしていて、「21」になるよ。
じっさいに進んだのは1マスだったので、ズレは「-20」だね。
つまり、負けてしまったことによってのマイナス分が「20」あるんだ。
この「20」は、長方形BとCをたしたものになるよ。
どうして、「BとCをたすの?」とふしぎに思うかもしれないね。
なぜなら、「勝ったら3すすめる」のに、「負けたら2もどらなくてはいけない」というとき、2つの差は「5」になるから。
「負けたことで3すすめない=3を失う」「2もどらなくてはいけない=さらに2失う」ので、合計5つ分失うことになるからだね。
長方形BとCをたした面積が「20」になるということは、縦は5なのだから、
20÷5=4で
横は「4」だということがわかるね。
なので、負けた数は4回、
勝った数は3回だよ。
つるかめ算と方程式
小学校で学習するつるかめ算だけれど、これってじつは中学校数学で学習する「方程式」のひとつなんだ。
「方程式」とは、「いくつなのかわからないもの」を「X」や「Y」などの文字でかりにあらわしてあげて、○○=××という「イコールの関係(等式というよ)」からそれぞれの「いくつなのかわからないもの」をもとめる式のこと。
つるかめ算の説明をするときにも、「✩」とか「△」を使ったよね。
この「✩」とか「△」のかわりに「X」や「Y」などの文字を使っているだけだよ。
そして、「つるとかめが合わせて11ぴき」のことを、何匹いるのかわからないつるを「X」、何匹いるのかわからないかめを「Y」として、
x+y=11
とするんだ。これが等式だよ。
さらに、「つるとかめの足の数を合わせると28本」のことを、「2本足のつるがX匹(2×X)」、「4本足のかめがY匹(4×Y)」として、
2X+4Y=28
とするよ。これがもうひとつの等式になるよ。
中学校の数学では、このように2つの等式があって、それぞれおなじ「X」と「Y」でできているばあい、2つの等式を組み合わせて「連立方程式(れんりつほうていしき)」というやりかたで「X」と「Y」をパパっともとめてしまうことができるんだ。
じっさいにやってみるね。
ただ、これは中学校で学習する内容なので、こまかいところまで説明すると大変なことになってしまうので、ざっくりと説明するよ。
2x+4y=28
x+y=11
上の等式から下の等式を引いて、「x」をなくしてしまうために、下の等式全体に2をかけるよ。
2x+4y=28
2x+2y=22
上の等式から下の等式を引くよ。
2x+4y=28
-)2x+2y=22
2y=6
y=3
xをどちらも「2x」にしたことで、上の等式から下の等式を引くと、「2x-2x」になって、xはなくなるんだ。
yは「4y-2y」で「2y」、「28-22」は「6」になるよ。
こうすることで、「2y=6」になって、「yに2をかけると6になる」ということは、「yは3である」ことがわかるんだ。
yが3なので、xは「11-3=8」で8だということがわかるね。
どうだろう?連立方程式をつかうと、つるかめ算はあっという間にとくことができるね。
中学受験で、つるかめ算を方程式を使ってといてもいいのか?
中学受験をするばあい、むずかしいつるかめ算が問題に出る可能性は高いよね。
そんなとき、いっそのこと方程式を使ってしまえばかんたんになる場合もあるよね。
結論からいうと、受験のときに「方程式を使ってはいけない」とハッキリ禁止している学校はないんだ。(2024年4月現在)
なので、方程式のやりかたを覚えてしまうのもひとつのワザかもしれないね。
ただ、方程式で考えようとすると逆にややこしくなったり、そもそも方程式を理解するのが大変すぎたりすることもあるので、そこは注意したいところ。
「どうしてそういう計算でもとめることができるのか」といういちばん大切なことをきちんと理解するためにも、まずは つるかめ算をしっかりとマスターすることも必要だね。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。



