「長方形のたての長さと面積の関係」周が同じでも面積が変わる理由
小学校4年生の算数で学習する「面積」について、長方形と正方形の周りの長さと面積にはどういう関係があるのかをわかりやすく解説するよ。
周りの長さが同じでも、四角形が正方形に近づくにつれて面積が増えるのはなぜか、くわしく紹介しているよ。
周りの長さが同じ四角形の面積
長方形と正方形の面積の求め方を学習したね。
このページでは、長方形と正方形の周りの長さと、面積にはどういう関係があるかを学習するよ。
次の3つの長方形を見てみよう。
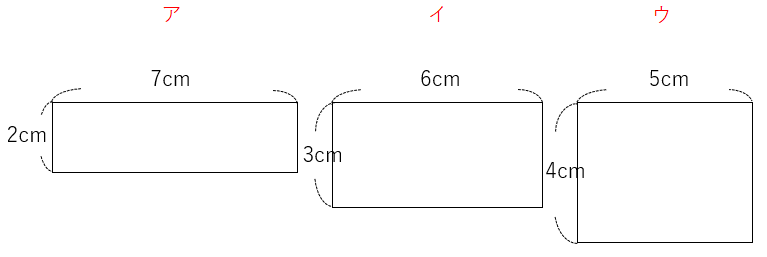
長方形アの周りの長さは2+7+2+7=18cm
長方形イの周りの長さは3+6+3+6=18cm
長方形ウの周りの長さは4+5+4+5=18cm
3つとも、「周りの長さが18cm」で同じだね。
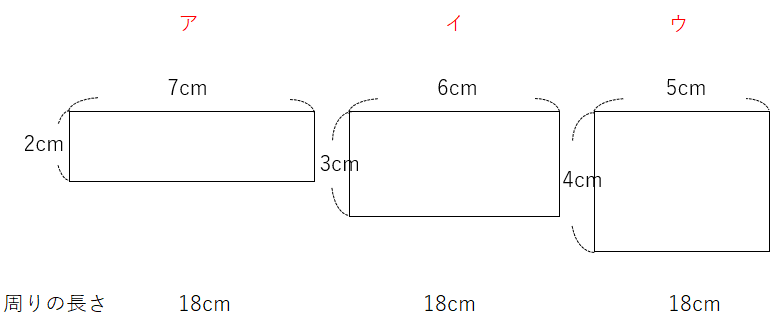
では、この3つの長方形の面積を計算してみよう。
周りの長さが同じなんだから、もちろん面積も同じだと思うよ。
長方形の面積は「たて×横」で求めることができるよね。
長方形アの面積は2×7=14cm2
長方形イの面積は3×6=18cm2
長方形ウの面積は4×5=20cm2
なんと周りの長さが同じなのに、面積はちがうんだ。
3つの長方形の周りの長さと面積の関係をまとめると次のようになるよ。
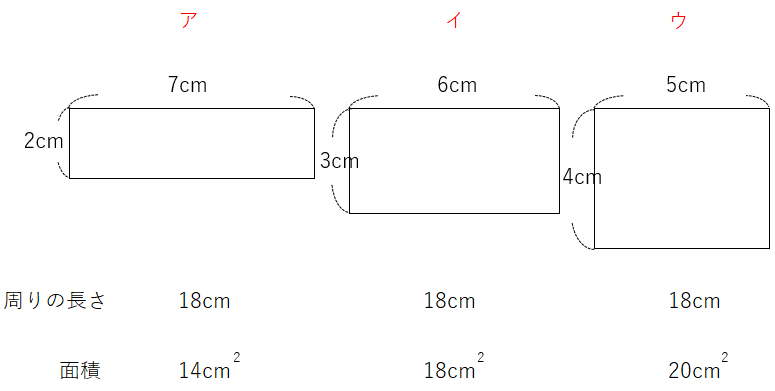
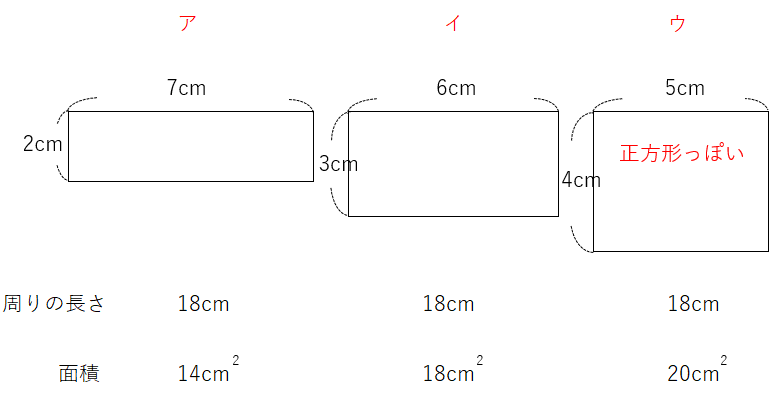
3つの長方形の周りの長さと面積の関係から、次のことがわかるよ。
長方形の「たて」と「横の長さ」が同じくらいになっていくと、だんだん面積は大きくなる。
もっとわかりやすくいうと、
周りの長さが同じでも、「正方形っぽく」なるにつれて、面積は大きくなっていくんだ。
今度は、長方形と正方形では「周りの長さと面積の関係」がどうなっているのかを求めてみよう。
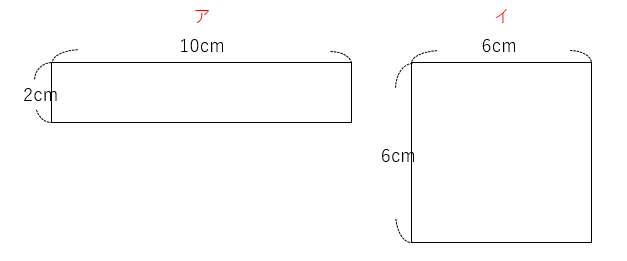
アの周りの長さは2+10+2+10=24cm
イの周りの長さは6+6+6+6=24cm
アは長方形で、イは正方形だけれど、2つとも周りの長さは24cmでおなじだね。
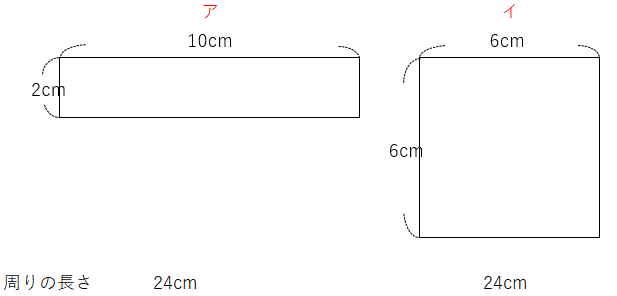
それでは2つの図形(長方形と正方形)の面積を計算してみよう。
長方形の面積は「たて×横」、正方形の面積は「1辺×1辺」で求めることができるから、
アの面積は2×10=20cm2
イの面積は6×6=36cm2
周りの長さはおなじでも、やっぱり面積はちがうんだね。
2つの図形の周りの長さと面積の関係をまとめると次のようになるよ。
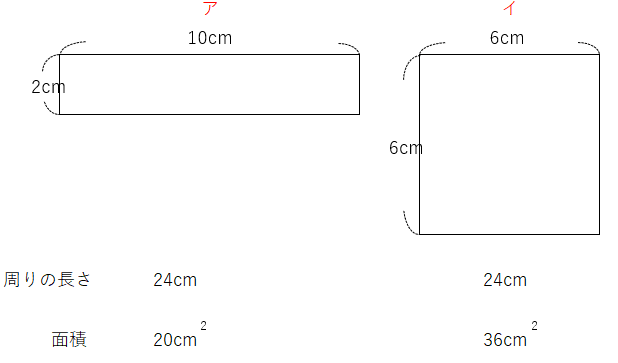
2つの図形の周りの長さと面積の関係から、次のことがわかるよ。
「たて」と「横の長さ」が同じになると面積は大きくなる。
もっと、わかりやすくいうと、
周りの長さが同じでも、正方形になると、面積は大きくなっていく。
やっぱり、さっき説明した関係がなりたっていることがわかるね。
長方形の長さと面積の関係
- 周りの長さが同じでも、正方形に近づくにつれて面積は大きくなる
正方形に近づくと面積が大きくなる理由
周りの長さが同じでも、正方形に近づくにつれて面積が大きくなることがわかったけれど、なぜそうなるのかフシギだよね。
少しむずかしい説明にってしまうのだけれど、なぜ正方形に近づくと面積が大きくなるのかを説明するよ。
長方形の面積を、1cm2の正方形であらわしてみるよ。
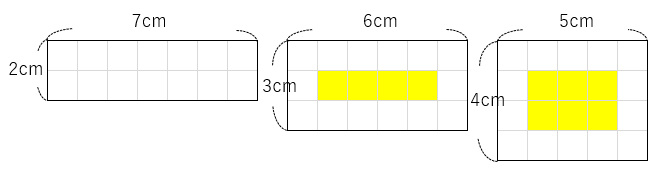
長方形の周りの部分の正方形を白い正方形だとすると、「周りの長さが同じ」というのは、「白い正方形の数が同じ」ということだよね。
ただ、図を見てわかるとおり、周りの長さが同じでも形が正方形に近づくにつれて白の長方形にかこまれている「黄色の正方形」の数がふえていくよね。
黄色の正方形の部分が増えるほど、面積も大きくなっているということだよね。
だから、正方形に近づくにつれて面積が大きくなるんだよ。
正方形に近づくと、周りに囲まれる部分が増えるから面積が大きくなるんだね。
長方形と正方形で比べても、同じことがいえるよ。
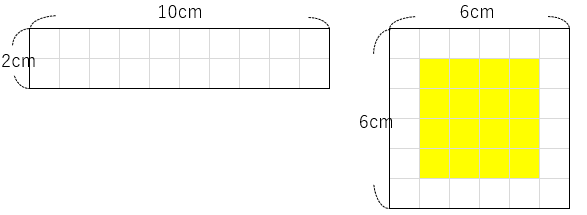
周りの長さ(白い正方形の数)が同じでも、正方形は周りに囲まれる部分(黄色い正方形の数)が増えていることがわかるね。
長方形の長さと面積の関係を使った問題
運動場に長さが20mのひもで長方形または正方形のコートを作ります。一番面積が大きくなるのは、たてと横の長さがそれぞれ何mのときになるかを答えなさい。
周りの長さが同じでも、正方形に近づくにつれて面積が大きくなるのだから、
できるだけ正方形になるように、たてと横の長さを考えればいいんだよね。
20mのひもで長方形または正方形のコートを作るということは、できあがるコートの周りの長さは20mになるということだよね。
長方形も正方形も4辺あるので、周りの長さを4で割ればいいね。
20÷4=5で割り切れるので、
1辺は5mになるね。
4辺がおなじ長さなので、できあがるコートは正方形だね。
問題では「コートの面積が一番大きくなるのは、たてと横の長さがそれぞれ何mのときか」ときかれているので、答えは「たて5m、横5mのとき」だね。
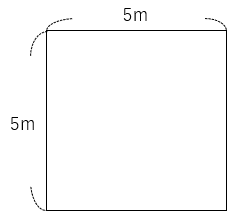
ちなみに面積は5×5=25cm2とわかるよ。
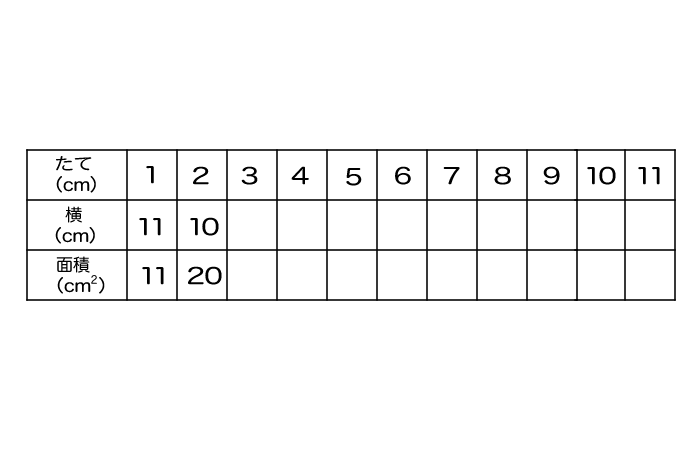
周りの長さが24cmになるように、長方形や正方形をつくります。
下の表をうめなさい。
たての長さがわかっているので、それをもとに横の長さと面積を求めればいいんだね。
長方形と正方形は、向かい合う辺の長さはおなじだから、「たてが3cm」だったら、たての辺が2辺で、3×2=6cmになるね。
周りの長さが24cmだから、たての2辺ぶんの6cmを引くと、
24-6=18で、横の長さは2辺合わせて18cmということがわかるね。
ということは、1辺の横の長さは、18÷2=9cmだよね。
さらに長方形の面積は「たて×横」で求められるから、
3×9=27cm2とわかるよ。
あとは、たてが4cm~11cmも同じように計算すると、表は次のようになるよ。
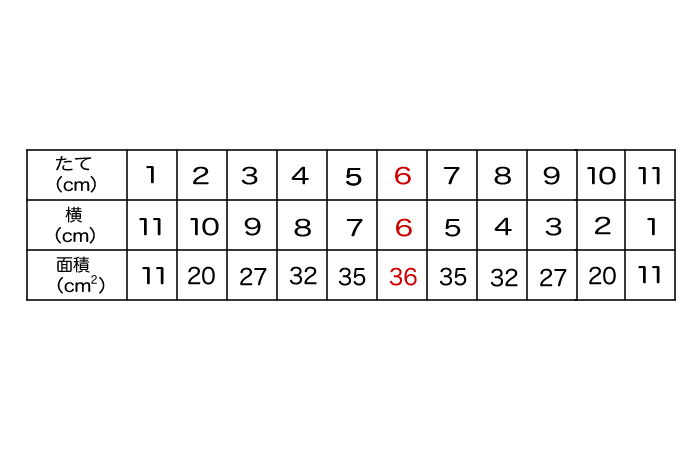
この表を見ても、やっぱり「たて6cm、横6cm」の正方形ときが一番面積が大きくなっているね。
逆に、長方形が細長い形(たて長または横長)になればなるほど、面積は小さくなっているね。
ちなみに今回は平面な図形(ぺたんこで、高さがない図のこと)だったけれど、もうすこし先に学習する立体な図形(サイコロや箱のように、たて・横・高さがある図形のこと)ではどうだろう?
たとえば下の2つの立体図形が、周りの長さが同じだったとしたら、どっちのほうが「大きい(たくさん入る)」と思うかな?
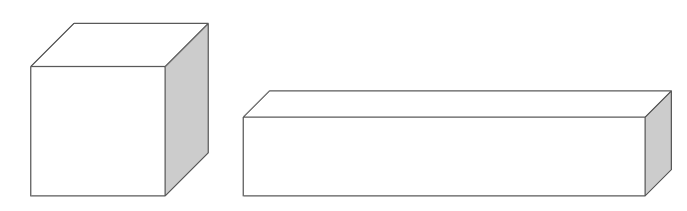
答えは、左の正方形のような形のほうが大きいんだ。
平面な図形のときとおなじで、「周りの長さが同じでも、正方形の形に近づくにつれて大きくなっていく」んだね。
「長方形の長さと面積の関係」まとめ
「長方形の長さと面積の関係」
- 周りの長さが同じでも、たてと横の長さが同じになっていくにつれて面積は大きくなっていく。
- 周りの長さが同じでも、正方形に近づくにつれて面積は大きくなっていく。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。




非常にわかりやすかったです。
長年モヤモヤしてたものが
スーと落ちて行きました。笑