「１０倍した数と１０分の１にした数」整数の表し方を考えてみよう

小学校４年生の算数で学習する「整数の表し方」について、整数を１０倍にしたとき、位がどのように変わるのか、整数を１０分の１にしたときに位がどのように変わるのか、数字を使って整数を表すときの考え方などをわかりやすく解説するよ。

「１０倍した数と１０分の１にした数」 整数の表し方を考えてみようのPDF（13枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 整数を１０倍にしてみよう
• 整数を１０分の１にしてみよう
• 整数の表し方
• まとめ

整数を１０倍にしてみよう

整数を１０倍した数について求めて、位くらいがどのように変わるのかを考えていこう。

まず、２５０億を次のように表そう。
「２５０億」を数字で表すと、「２５０００００００００」だね。

四角の中に書くのが大切というわけではなくて、「大きな数のしくみ」で学習したとおり、大きな数は「一・十・百・千」の４つをくりかえしていて、その後ろにつくのが「万」「億」「兆」なので、「２５０億」を右から４つずつ区切って表すことがポイントだよ。

さて、話はもどって、数を「１０倍する」ということは、「０」が１つふえるだけだね。
例えば、「２０」を１０倍したら「２００」になるよね。

では、「２５０億（２５０００００００００）」に、０を１つふやしてみよう。

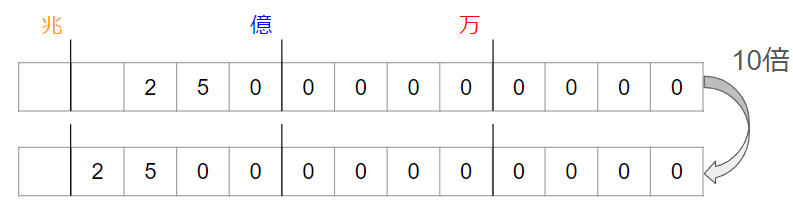
上の図から、２５０億を１０倍した数は２５００億になることがわかったね。

１０倍するということは、「０」が１つふえるだけだから、３０億を１０倍した数は３００億になることがわかるよ。

たろう

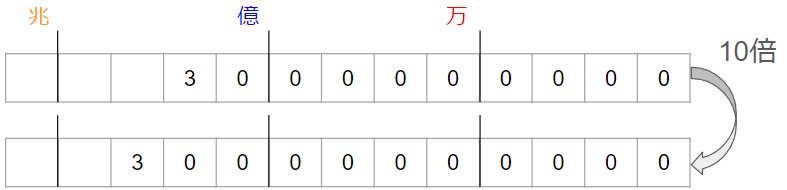
１０倍するときは「０」を１つふやすだけと覚えていれば、かんたんな問題なんだね。

ただ、気をつけなくてはいけない場合もあるんだ。

さっきの考え方だと、「０」が１つふえるだけだから、
「３０００億を１０倍した数は３００００億かな？」
と思ってしまう人もいるかもしれないね。

下の図を見てたしかめてみよう。
※図に書けなくても、右から「４ケタずつ区切って」考えてみてね。

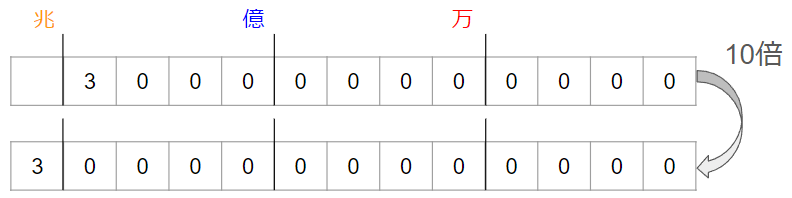
「一・十・百・千」をくりかえしているから、３０００億のつぎの位は、「兆」になってしまうよね。

だから、３０００億の１０倍は、「３００００億」ではなくて、「３兆」になるよ。

数を１０倍するときは、ただ「０」を１つふやすだけではなく、「万」「億」「兆」の区切りも変わらないかどうかも考えるようにしよう。

整数を１０倍したときの位

「１０倍にする」ことを、「０が１つふえる」と説明してきたけれど、これはつまり「位が１けた上がる」ということだよね。

整数を１０倍すると、位は１けた上がるんだね。
さっきやった２問をもう一度見てみよう。

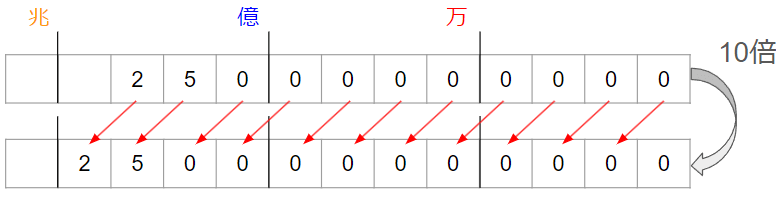
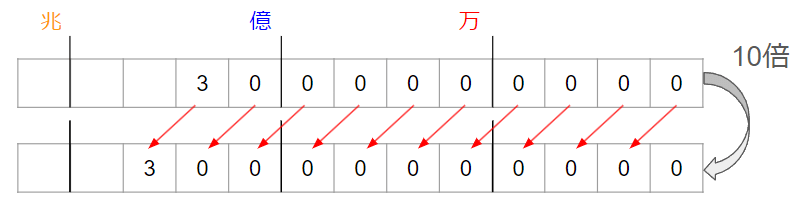
すべての位の数が左に動いていることがわかるね。
左に動くというのは、「位が１けた上がること」だよ。

ちなみに、
整数を「１００倍」すると、位は「２けた上がる」よ。
整数を「１０００倍」すると、位は「３けた上がる」よ。
よゆうがあったら覚えておこうね。

整数を１０倍したときのポイント

整数を１０分の１にしてみよう

それでは今度は、整数を\(\frac{１}{１０}\)にした数について求めて、位がどのように変わるのかを考えていこう。

２５０億は、数字に表すと「２５０００００００００」だったね。
区切りに注目して表してみるよ。

「\(\frac{１}{１０}\)する」ということは、「１０でわる」ことと同じだね。
「１０でわる」ということは、「０」が１つへるだけだね。
例えば、「２０」を１０でわったら「２」になるよね。

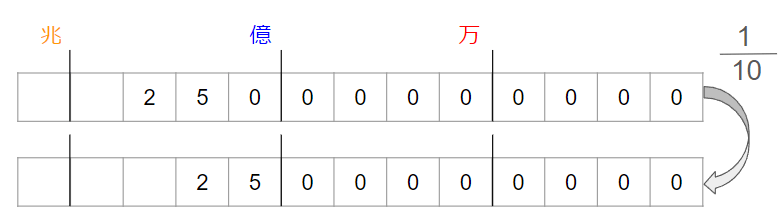
上の図から、２５０億を\(\frac{１}{１０}\)にした数は２５億になることがわかったね。

「\(\frac{１}{１０}\)にする」ということは、「０」が１つへるだけだから、
４０億を\(\frac{１}{１０}\)にした数は４億になることがわかるよ。

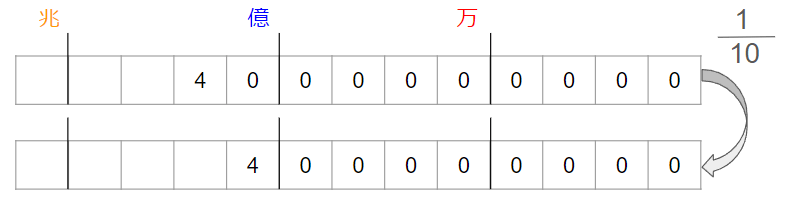
\(\frac{１}{１０}\)にするときは「０」を１つへらすだけと覚えていれば、
かんたんな問題だよね。

\(\frac{１}{１０}\)にするときも、「４つの区切りが変わらないか」は注意しておこうね。
たとえば、４０億を\(\frac{１}{１０}\)にした数は４億になるけれど、
４億を\(\frac{１}{１０}\)にした数は「億」から区切りが変わって、４０００万になるので気を付けよう。

整数を１０分の１にしたときの位

「\(\frac{１}{１０}\)にする」ことを、「０が１つへる」と説明してきたけれど、これはつまり「位が１けた下がる」ということだよね。

整数を\(\frac{１}{１０}\)にすると、位は１けた下がるんだ。
さっきやった２問をもう一度見てみよう。

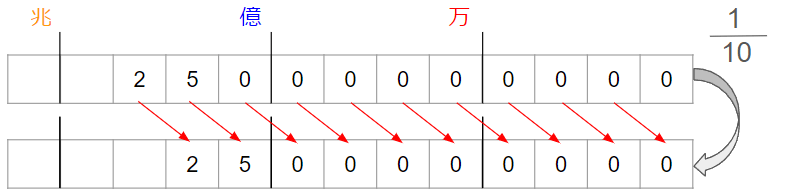
すべての位の数が右に動いていることがわかるね。
「右に動く」というのは、「位が１けた下がる」ということだよ。

ちなみに、
整数を「\(\frac{１}{１００}\)」にすると、位は「２けた下がる」よ。
整数を「\(\frac{１}{１０００}\)」にすると、位は「３けた下がる」よ。
よゆうがあったら覚えておこう。

整数を１０分の１にしたときのポイント

整数の表し方

今まで、整数を１０倍や\(\frac{１}{１０}\)にしたときの表し方を学習してきたね。

今度は、数字を使って整数を表すときについて考えてみよう。

整数は、どんな大きな整数でも０、１、２、３、４、５、６、７、８、９の１０この数字を使えば表すことができるんだ。

くまごろう

だから、電たくも０～９の数字のボタンが１つずつあるんだよ。

では、次の整数の表し方についての問題にちょうせんしてみよう。

「１０けたの整数」だということは、次のように赤でかこったところまで数字が入るってことだよ。
右から数えたときに、１０こ目になるところまでだね。

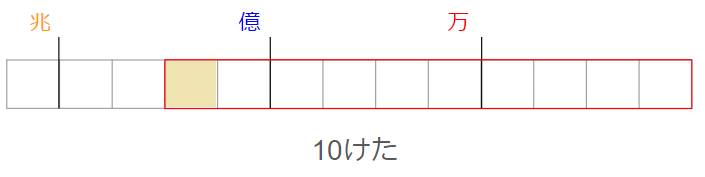
「５番目に大きい数」を探さなくてはいけないので、まずは１番大きい数から見つけていこう。

１０けたの整数を作るので、まずは一番最初（左）の数から決めていくよ。
黄色にぬったところだね。

１番大きい数を見つけなければいけないので、ここに入る数をできるだけ大きくする必要があるね。

使えるのは「０～９」までの数字なので、「０～９」の中で一番大きい「９」が入るよ。

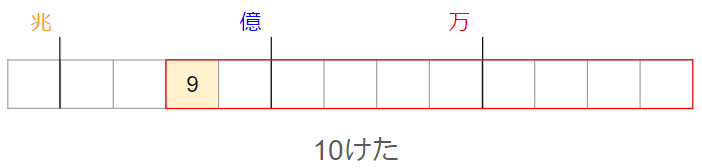
他のけたに入れる数字も同じように考えると、「０～９」の中で一番大きい「９」を入れていけばよいよね。

そうすると、１０けたの整数で１番大きい数は
「９９９９９９９９９９」になるよ。

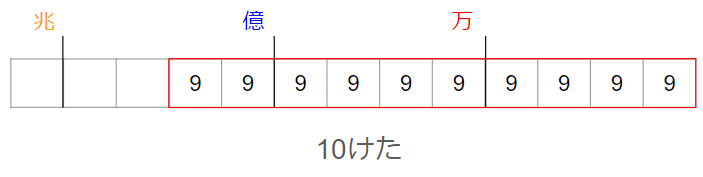
今回の問題で探さなくてはいけないのは、「５番目に大きい数」だったね。

「９９９９９９９９９９」が一番大きい数なのだから、あとは一の位が小さくなると、１０けたの整数もだんだん小さくなっていくから５番目に大きい数は次のようになるよ。

答えは９９９９９９９９９５だね。

では、少しむずかしい問題にちょうせんしてみよう。

「０」から「９」までの数字カードが１まいずつあります。

１０まいのカードをならべて、１０けたの整数を作るとき、一番大きい数と、一番小さい数を答えなさい。

さっきの問題とちがうのは、０～９の数字が１回ずつしか使えないということなんだ。
だから、「９９９９９９９９９９」を作ることはできないね。

一番大きい数を探してみよう

さっきの問題と同じで、
１０けたの整数で大きい数を作るときは、黄色に入る数ができるだけ大きくする必要があるね。
なので、黄色には「９」が入るよ。

次は緑に入る数を考えるんだけど、さっきと違うのは、もう「９」が使えないということだね。
なので、残った０～８の中で一番大きい「８」が入るよ。

他のけたでも同じように考えると、１０けたの整数で一番大きい数は
９８７６５４３２１０になるよ。

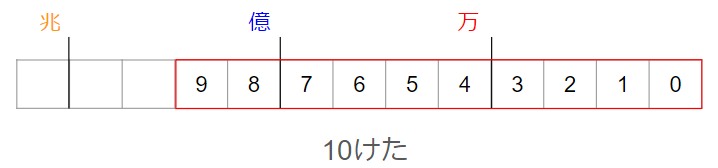
一番初め（左）から、できるだけ大きい数から順番に使っていけばいいんだね。

一番小さい数を探してみよう

一番小さい数を探すには、一番大きい数を探したときと「ぎゃく」で考えたらいいと思うかもしれないね。
でも、１つ気をつけなくてはいけないことがあるんだ。
それは、１０けたの「整数」を作るので、「０」から始めてはいけないということ。整数は「０」から始まらないからね。

「０」が使えないということは、始めの数は、「０」の次に小さい数の「１」になることがわかるね。

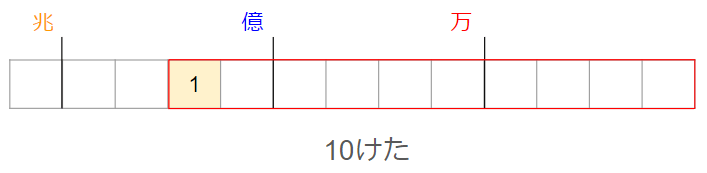
次は緑に入る数を考えるんだけれど、ここも注意するポイント。
「１」次に小さい「２」が入るんだ！とあせってはいけないよ。

なぜなら、２番目のけたなら「０」が使えるから。
使えるのであれば、できるだけ小さい数を使いたいので、ここで「０」が入るよ。

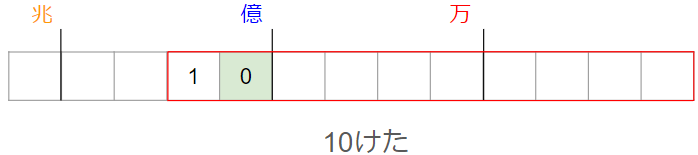
次こそ「２」が入って、その次は「３」が入って・・・

他のけたでも同じように考えていくと、１０けたの整数で一番小さい数は
「１０２３４５６７８９」になるよ。

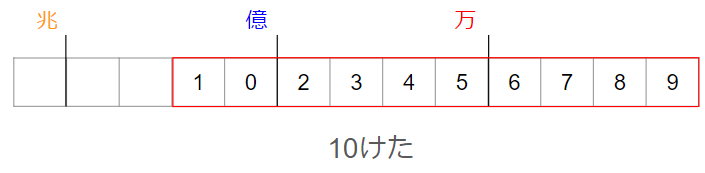
「１回ずつしか使えない」というルールがあったり、「０から始めてはいけない」など、問題をよく読んで、おちついて考えれば大丈夫。
いろいろな問題のパターンになれておくと、あんしんだよ。

「１０倍にした数、１０分の１にした数」「整数の表し方」まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。