面積の求め方の工夫（複合図形の面積の求め方）をわかりやすく解説

小学校４年生の算数で学習する「複合図形の面積の求め方」について、いくつかの図形が組み合わさった図形の面積を、長方形と正方形の面積の求め方を使って工夫して求める方法をわかりやすく解説するよ。

面積の求め方の工夫（複合図形の面積の 求め方）をわかりやすく解説のPDF（7枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

面積の求め方のくふう（複合図形の面積の求め方）

長方形の面積の求め方と、正方形の面積の求め方を学習したね。

長方形の面積の公式

・たて×横

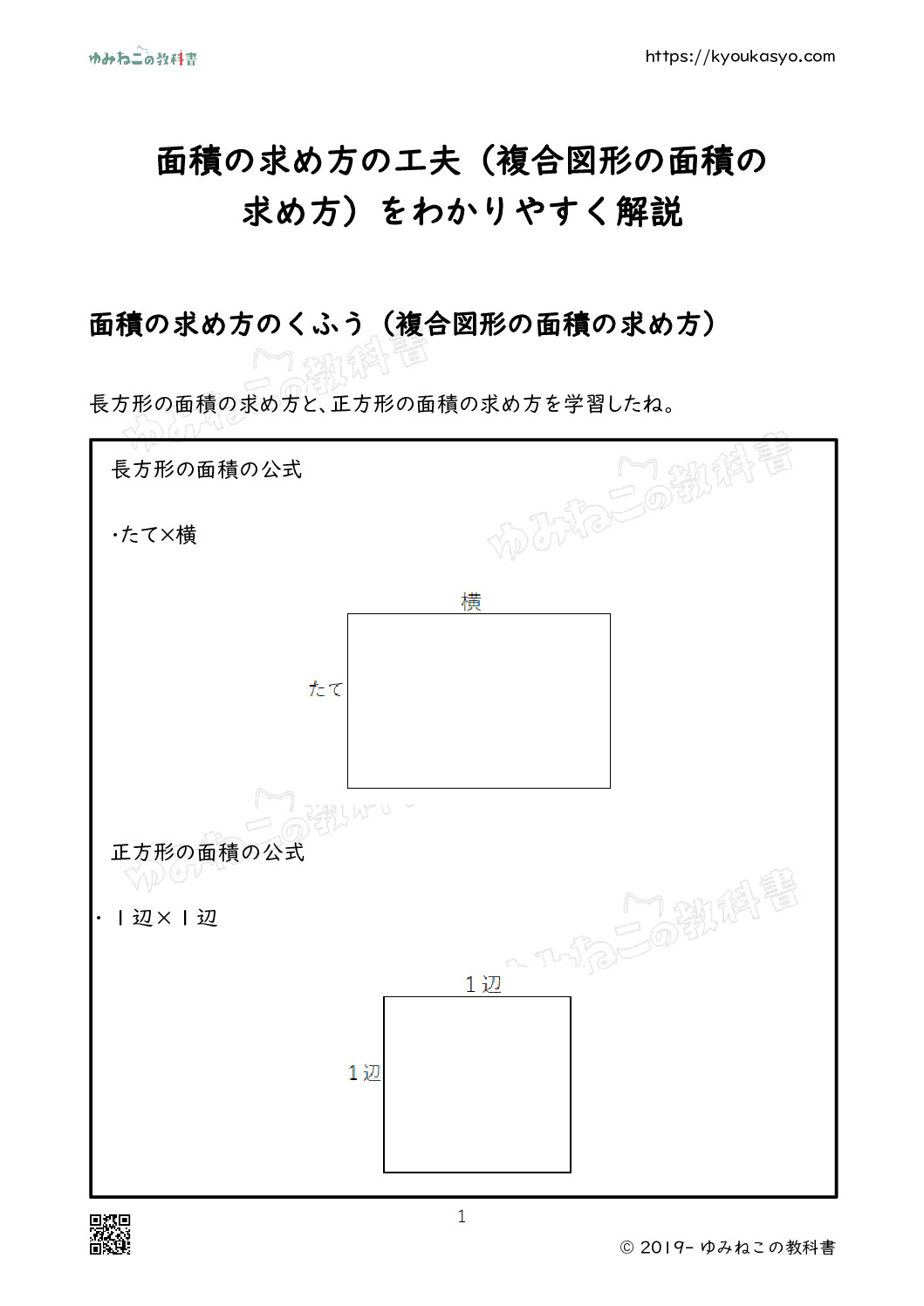
正方形の面積の公式

・１辺×１辺

長方形と正方形の面積の求め方がわかれば、くふうして、すこし変わった形の図形の面積が求められるようになるんだ。
※このようなすこし変わった形の図形を、複合図形というよ。

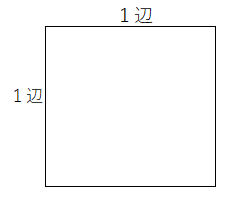
たとえば、つぎの図形の面積を求める問題を考えてみよう。

次の面積を求めなさい。

たろう

長方形でもないし、正方形でもない図形だから、どうやって求めるのかわからないよ。

くまごろう

長方形の面積の求め方を使ってくふうすれば、求めることができるよ。

くふうのやり方には、おおきくわけて２つの方法があるよ。
１つは「図形と図形をたす」やり方、もう１つは「図形から図形を引く」やり方だよ。

図形と図形をたして面積を求めるやり方

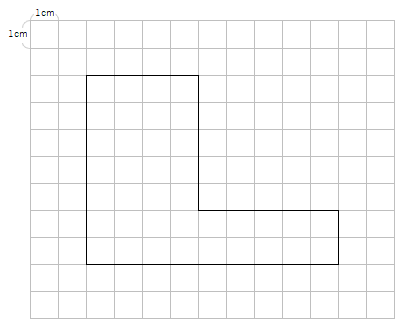
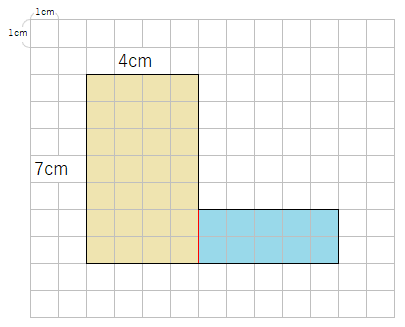
問題の図形を、黄色の長方形と、青の長方形にわけてみたよ。
これならどうかな？
※わけかたは、他にもあるよ。ポイントは、「わけたあとの図形が、ぜんぶ長方形か正方形になっているようにする」ことだよ。

黄色の長方形の面積と、青の長方形の面積はそれぞれ「たてと横」がわかるから、長方形の面積の公式を使って面積を求めることができるよね。

それぞれの長方形の面積を求めたら、２つの面積を合わせれば、もとの図形の面積になるよね。

それでは、それぞれの面積をじっさいに求めてみよう。

黄色の長方形の面積を求めよう

黄色の長方形は、たてが７ｃｍ、横が４ｃｍだから、
長方形の面積の公式「たて×横」を使って、
面積は７×４＝２８ｃｍ^２と求めることができるね。

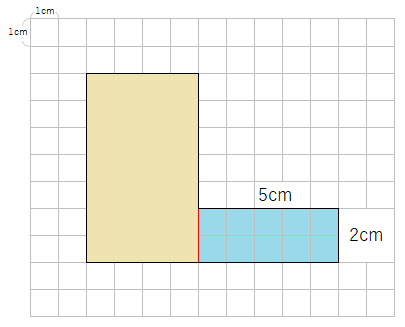
青の長方形の面積を求めよう

青の長方形は、たてが２ｃｍ、横が５ｃｍだから、
面積は２×５＝１０ｃｍ^２と求めることができるね。

求めた２つの長方形の面積を合わせよう

黄色の長方形（２８ｃｍ^２）と青の長方形の面積（１０ｃｍ^２）をたすと、
２８＋１０＝３８ｃｍ^２
と求めることができるね。

答え：３８ｃｍ^２

図形から図形を引いて面積を求める方法

今度は、図形から図形を引く方法をしょうかいするね。

次の面積を、先ほどとはちがう方法で求めなさい。

この図形って、かけているところ（へこんでいるところ）をなくしたら、大きな長方形になるよね。

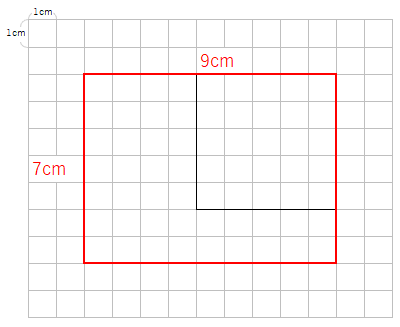
今回の問題で求めなければいけないのは、黄色でぬった部分だから、赤い長方形から、右上の白い部分の面積を引けばいいよね。
赤い長方形も、白い部分も、「たて」と「横」が分かっているから、面積を求めることができるね。

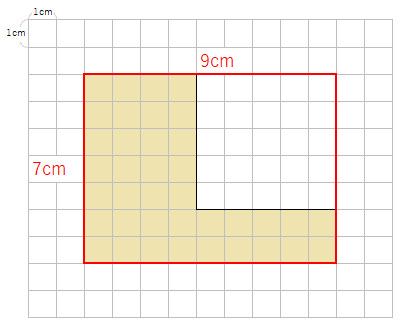
赤い長方形の面積を求めよう

赤い長方形は、たてが７ｃｍ、横が９ｃｍだから、
７×９＝６３ｃｍ^２で、
赤い長方形の面積は６３ｃｍ^２だとわかったね。

白い部分の面積を求めよう

白い部分は、１辺が５ｃｍの正方形だから、
５×５＝２５ｃｍ^２で、
白い部分の面積は２５ｃｍ^２だとわかったね。

赤い長方形の面積から、白い部分の面積を引こう

赤い長方形の面積（６３ｃｍ^２）から、白い部分の面積（２５ｃｍ^２）をひけば、黄色い部分の面積になるから、
６３－２５＝３８ｃｍ^２
と求めることができるね。

答え：３８ｃｍ^２

面積の求め方のくふう（複合図形の面積の求め方）まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。