「およその数（がい数）」とは？表し方と求め方（練習問題）

小学校４年生の算数で学習する「およその数（がい数）」について、およその数とは何か、どういう時に使うのか、およその数の表し方と求め方をわかりやすく解説するよ。

四捨五入のやり方、以上・以下・未満の言葉の意味と練習問題も紹介しているよ。

「およその数（がい数）」とは？ 表し方と求め方（練習問題）のPDF（15枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 「およその数」とは（がい数）
• 「およその数」を使う場面
• 「およその数」での表し方
• 「四捨五入」とは
• 「およその数」の練習問題
• 「以上・以下・未満」とは
• 「以上・以下・未満」の練習問題
• まとめ

「およその数」とは（がい数）

小学校４年生では、「およその数（がい数）」という言葉を学習するよ。
「およそ」は、漢字だと「凡そ」と書くんだ。
「凡」という漢字には、「いいかげん」という意味があるよ。

つまり、「およその数」とは、「ザックリ表した数」のことなんだ。

くまごろう

「がい数」は、漢字だと「概数」と書くよ。
「概」という漢字には「だいたい」という意味があるよ。

ふだんの生活でも、「およそ２００００円」「だいたい４０%」「ほぼ１０００人くらい」なんて言葉を聞いたことがあるよね。

どれも正かくな数ではなくて、およその数だね。

「およその数」を使う場面

およその数（がい数）を使う場面は、大まかに「数の大きさ」を表したい時だよ。

たとえば、別の小学校の友達に「あなたの小学校の人数は何人？」と聞かれたときに、
正確に「２３１２人」
と答えるよりも、
「およそ２０００人」
と言った方がわかりやすいときもあるよね。

だって、別の小学校の友達は正かくな人数を知りたいわけではないからね。

「およその数」での表し方

数をザックリと伝えるといっても、本当に適当に伝えてしまったら良くないよね。
たとえば、本当は２３１２人なのに、
「うーん・・まあ１０００人くらいかな」
なんて伝えてしまったら、本当の数を知った友達は、
「全然ちがうじゃん！」と怒るかもしれないね。

では、「およその数」で表すには、どうすればいいのかな？

たとえば、「２３１２」という数字を数直線で考えてみよう。
２３１２は、２０００と３０００の間にあって、３０００よりも２０００の方に近いよね。

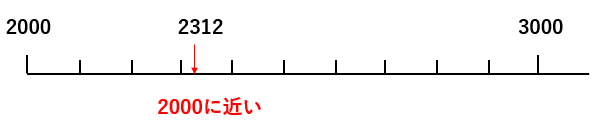
だから、「２３１２人」は「およそ２０００人」と言えるんだね。

ちなみに、もし「２６５３人」だったらどうだろう？
２６５３は２０００と３０００の間にあって、３０００の方が近いね。

なので、「２６５３人」のおよその数は３０００人と言えるんだね。

ここまでは「ふんふん、そうだよね。」となっとくできるよね。
では、「２５００人」だったらどうだろう？
「およそ２０００人」なのかな？それとも、「およそ３０００人」かな？

「２５００」は、「２０００」と「３０００」のちょうど真ん中だよね。
これでは、どっちを選んでいいのかこまってしまうね。

そんなときに大切な考えかたが「四捨五入ししゃごにゅう」なんだ。

「四捨五入」とは

「四捨五入」と聞くと、なんだかとっても難しそうだよね。
でも、どういうことなのか、漢字が意味をわかりやすく表してくれているよ。

「四捨ししゃ」・・・４は捨すてる＝４までは切り捨て
「五入ごにゅう」・・・５は入いれる＝５からは切り上げ

ここで「切り捨て」、「切り上げ」という言葉がでてきたね。

イメージがつきにくいと思うから、じっさいに問題をみてみよう。

たとえば「２０００」、「２１００」、「２２００」、「２３００」、「２４００」という５つの数字を百の位で四捨五入するとするよ。

それぞれ百の位の数字は「０」「１」「２」「３」「４」だね。
四捨五入は、「４までは切り捨て」だったよね。
だからぜんぶ「切り捨て」になって、指定された「百の位」と、その下の「十の位」と「一の位」が「０」になって、どれも「２０００」になるよ。

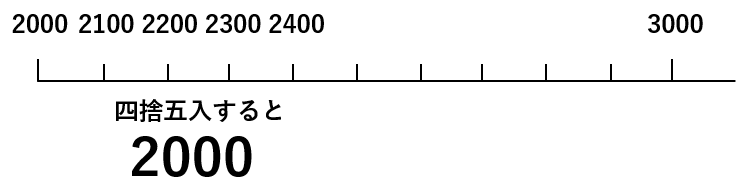
では、「２５００」、「２６００」、「２７００」、「２８００」、「２９００」の５つの数字はどうだろう。

それぞれの百の位の数字は「５」「６」「７」「８」「９」だね。
四捨五入は、「５から切り上げ」だったね。
だからぜんぶ「切り上げ」になって、１つ上の「千の位」に１を加えて、指定された「百の位」とその下の「十の位」と「一の位」は「０」になるよ。
つまり、ぜんぶ「３０００」になるんだ。

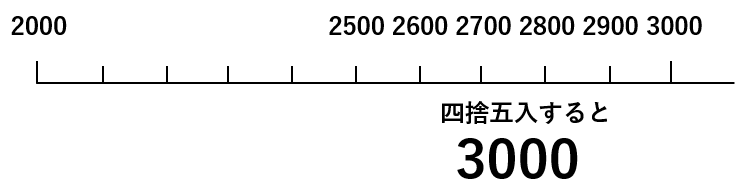
四捨五入についてまとめると次の通りだよ。

「およその数」の練習問題

では、四捨五入を使って、「およその数」の練習問題にちょうせんしよう。

四捨五入の時に気をつけることは、どの位を四捨五入するかだよ。
問題をときながら、かくにんしていこう。

「その位を四捨五入する」問題

「〇〇の位を四捨五入しなさい。」と、四捨五入する位を指定しているパターンの問題のときかたを練習しよう。

四捨五入するのは、「百の位」だね。
「３２５３」の百の位は「２」だよね。

「２」を四捨五入すると、「４までは切り捨て」だから、「２」は切り捨てだね。
指定された位（百の位）の「２」を「０」にしよう。

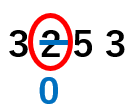
さらに、指定された位の下の位も「０」にしなくてはいけなかったね。
なので、四捨五入したけたの右にある数をぜんぶ「０」に変えよう。

３２５３の百の位を四捨五入すると、３０００になることがわかったね。

８６９４３の百の位は「９」だよね。

「９」を四捨五入すると、「５から切り上げ」だから、「９」は切り上げだね。
指定された百の位の上の位（千の位）に１を加えて、指定された百の位の「９」を「０」にしよう。

さらに、指定された位の下の位も「０」にしなくてはいけなかったね。
なので、四捨五入したけたの右にある数をぜんぶ「０」に変えよう。

８６９４３の百の位を四捨五入すると８７０００になることがわかったね。

「１つ下の位を四捨五入する」問題

「〇〇の位までのがい数にしなさい。」という問題は、「〇〇の位」の１つ下の位を四捨五入しよう。

「〇〇の位までのがい数にしなさい。」だなんて、むずかしい言い方で、ちょっとわかりづらいよね。
これは、つまり「○○の位までが知りたいよ。その下の位は、だいたいでいいよ。」という意味なんだ。

たとえば、あるゲームのソフトを買おうとしてるとするよ。
ゲーム屋さんに行くまえに、「いくらお金をもっていけばいいかな？」と思うよね。
それで、友達に「だいたい何千円かな？」と聞いたとするよ。
これって、「千円の位まで」が知りたいんだよね。何百円かまでは聞いていないよね。

もしゲームのソフトが３６８０円だったら、お友達はきっと「だいたい４千円だよ。」と答えてくれるよね。
「３６００円だよ。」だと細すぎるし、「１００００円だよ。」だと上の位すぎるよね。

「だいたい４千円」という数字は、「千円の位までが知りたいから、千円より下の百円の位を四捨五入」して表した数字だね。

さて、今回の問題は「５３４３４を四捨五入して、一万の位までのがい数」にするんだったね。

「一万の位まで」を知りたいのだから、その１つ下の千の位を四捨五入したらいいんだね。

５３４３４の、千の位は「３」だよね。

「３」を四捨五入すると、「４までは切り捨て」だから、「３」を「０」にしよう。

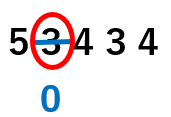
さらに四捨五入したけたの右にある数をぜんぶ「０」に変えよう。

５３４３４を一万の位までのがい数にすると５００００になることがわかったね。

「上から１つ目までのがい数にしなさい」という問題もさっきとやり方は同じだよ。
さっきは、「一万の位まで」とハッキリ教えてくれたけど、それを「上から１つ目まで」と言いかえているだけなんだ。

「一万の位まで」と言われたら、その１つ下の位を四捨五入するんだったね。
これが「上から１つ目まで」と言われても同じ。
つまり、その１つ下の位を四捨五入すればいいんだ。つまり、上から２つ目の位に注目しよう。

５７４３７の、上から２つ目の位は「７」だよね。

「７」を四捨五入すると、「５から切り上げ」だから、上の位に１を加えて、「７」を「０」にしよう。

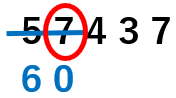
さらに四捨五入したけたの右にある数をすべて「０」に変えよう。

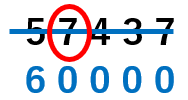
５７４３７を上から１つ目の位までのがい数にすると６００００になることがわかったね。

四捨五入する問題のポイント

問題によって、「その位を四捨五入する場合」と「１つ下の位を四捨五入する場合」があるから、まちがえないようにしよう。

ポイントは次の通りだよ。

「以上・以下・未満」とは

もうひとつ、あたらしい言葉を学習するよ。

遊園地に行ってジェットコースターに乗るときなどに、「１２０ｃｍ以上の人は乗れます。」「１２０ｃｍ以下の人は乗れません」「１２０ｃｍ未満の人は乗れません。」というような注意書きを見たことはないかな？

この「以上」「以下」「未満」はそれぞれ意味がちがうんだ。

「以上」とは

「以上」の「以」には次の意味があるよ。

だから、「以上」っていうのは
「あるところを始まりの場所として、それよりも上」のことなんだ。

つまり「１２０cm以上の人は乗れます。」と書かれていたら、１２０cmを始まりの場所として、それよりも身長が高い人は全員乗れるんだよ。
１２０cmを始まりの場所としているんだから、１２０cmの人も乗れるよ。

つまり、「１２０cm以上」という言い方の場合、「１２０cmの人もふくまれる」んだ。

「以下」とは

「以上」の「上」が「下」になっただけだから、かんたんだよ。

「１２０cm以下の人は乗れません。」だったら、１２０cmを始まりの場所として、それより低い人は全員乗れないんだ。（つまり１２０cmの人は乗れないよ）

「１２０cm以下」という言い方の場合、「１２０cmの人もふくまれる」んだね。

「未満」とは

「未満」と「以下」は、すごく意味が似ているからまちがえないようにしよう。

「未満」の「未」には次の意味があるんだ。

つまり、「１２０cm未満」だったら、「１２０cmになっていない」という意味になって、１２０cmの人はふくまれないんだ。

もし、「１２０cm未満のおこさまは、入場料が無料！」なんてサービスがあったとしたら、１２０cmになっていたら、無料にならないよ。

以上・以下・未満のまとめ

「以上・以下・未満」の練習問題

じっさいに、順番に一の位を四捨五入してたしかめてみよう。

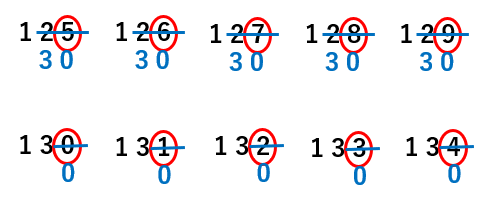
たしかに、「１２５」から「１３４」までの一の位を四捨五入してみると、「１３０」になったね。

問題文には「１３５以下」と書いてあるから、「１３５も四捨五入すると、１３０になる」と言っているんだよね。
でも、１３５は四捨五入すると、「５」は切り上げだから１４０になっちゃうよね。

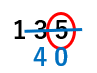
だから、「一の位を四捨五入して１３０になる範囲は、１２５以上１３５以下です。」という文章は「１３５以下です」という部分が正しくないことがわかったね。

では、どういう文章だったら正しいのかな？

「一の位を四捨五入して１３０になる範囲はんいは１２５以上１３４以下です。」だったら正しいのでは？と考えた人もいるかもしれないね。

ただ、これでもちがうんだ。
小数点以下まで考えてみよう。

たとえば、１３４.９という数を考えてみよう。
「１３４以下」とは、１３４を含む、それよりも少ない数のことだよね。
だから、１３４.１よりも大きい数は、「１３４以下」には入らないね。

でも、１３４.９は、一の位の「４」で四捨五入すると、１３０になるよね。

１３４.９９９という数を考えてみよう。
やっぱり、一の位の「４」で四捨五入すると、１３０になるよね。

つまり、１３４以下でなくても、１３５にさえならなければ、一の位で四捨五入したときに１３０になるんだ。

「１３５より大きくない数」は、どうやって言い表したらいいかな？

そう、「１３５には未だ満たない数」、「未満」を使えばいいんだよ。

だから、さっきの文章を正しくすると次のようになるよ。

「一の位を四捨五入して１３０になる範囲は１２５以上１３５未満です。」

これなら、１３５はふくまれないことになるよね。

「およその数の使い方と表し方」のまとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。