「平面上の点と空間にある点の位置の表し方」をわかりやすく解説位置の表し方
小学校4年生の算数で学習する「位置の表し方」について、平面上の点の位置の表し方と、空間にある点の位置の表し方をわかりやすく解説するよ。
「横」「たて」「高さ」をつかって、点の位置を表す方法を確認しよう。
平面上の点の位置の表し方
教科書で「位置の表し方」のページを見ると「なんだかむずかしそうだなー」と感じる人も多いと思う。
だけど、すごくかんたんな内ようだから安心してね。
「位置の表し方」は、かんたんに言うと「○○は、どこにあるかを説明しよう」ということなんだ。
「平面上の点の位置の表し方」は、「ペタンコの平らな面にある点が、どこにあるかを説明しようね」ということ。
ただ、その説明の方法にルールがあるので、そのルールを覚えればいいだけだよ。
平面上の点の位置を表すときには、( )をつかうんだ。
( )の中に何が入るのかというと、「横の長さ」や「たての長さ」が入るよ。
たとえば、じっさいの問題を見てみよう。
点Aをもとにすると、点Bの位置はどのように表せるか。
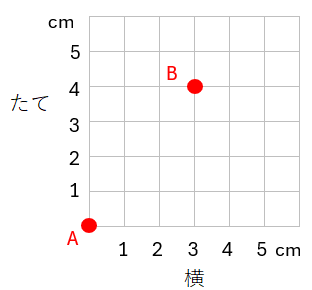
この問題では、「点Aから点Bまでどうやって行ったらいいか」を考えればOKだよ。
下のように、てきとうに行ってはいけないよ。
「平面上の点の表し方」では、「横」→「たて」の順にしか、行くことができないルールになっているんだ。
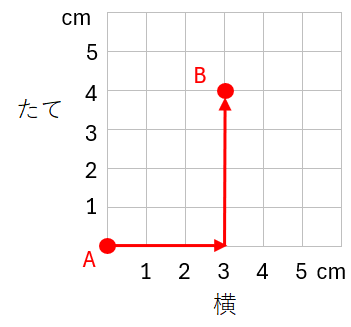
点Aから点Bに行くには、
まず、横に3cm行って、
そのあと、たてに4cm行けばいいよね。
だから、
点Aをもとにすると、点Bの位置は(横3cm、たて4cm)と表すことができるんだ。
横、たての順番をまちがえないようにしようね。
点Cをもとにすると、点Dの位置はどのように表せるか。
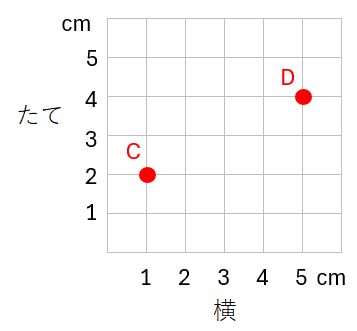
この問題では、「点Cから点Dまでどうやって行ったらいいか」を考えればOKだよ。
点Cから点Dに行くには、
まず、横に4cm行って、
そのあと、たてに2cm行けばいいよね。
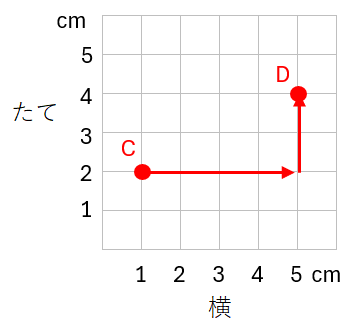
だから、点Cをもとにすると点Dの位置は(横4cm、たて2cm)と表すことができるんだ。
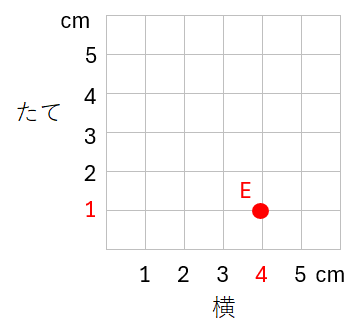
点E(横4cm、たて1cm)を下の図に書き入れなさい。
今までの問題とはちがうね。
点の位置が問題に書いてあるから、その点を書いたらいいんだ。
点Eは(横4cm、たて1cm)だから、
横が4cm、たてが1cmのところに点Eを書こう。
空間にある点の位置の表し方
「平面」はペタンコの平らな面だったから、「横とたて」だけでよかったよね。
それに対して「空間」ということは、「横とたて」にプラス「高さ」がふえるんだ。
でも、「どこに点があるかを説明する」ことはおなじだよ。
平面上の点の位置を表すときには( )をつかって、「(横、たて)」というふうに表したよね。
空間にある点の位置を表すときは、「(横、たて、高さ)」の順に表すよ。
点Aをもとにすると、点Bの位置はどのように表せるか。
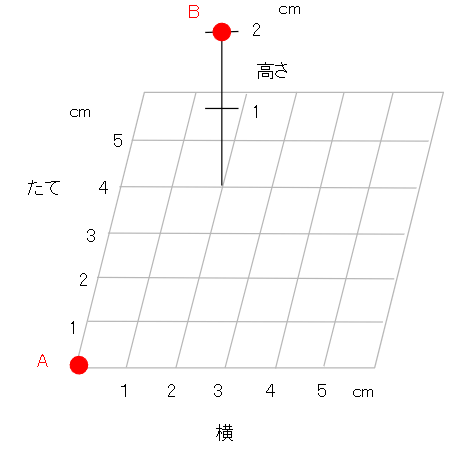
この問題では、「点Aから点Bまでどうやって行ったらいいか」を考えればいいね。
空間にある点の位置を表すときは、「(横、たて、高さ)」の順に表せばいいから、まずは、「横とたて」の順で、点Bの下の場所まで行こう。
横に2cm行って、たてに4cm行けば点Bの下の場所まで行けるね。
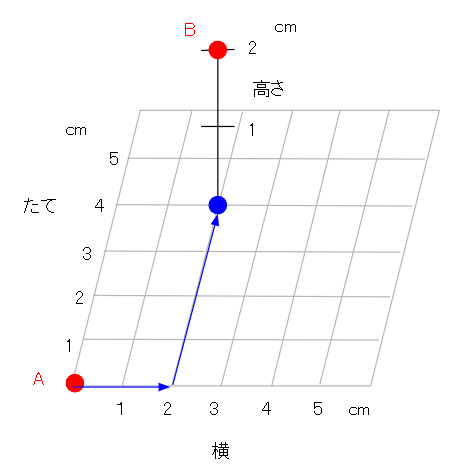
点Bの下の場所まで行ったら、あとは上に2cm行けば点Bのところに行けるね。
空間にある点の位置を表すときは、「(横、たて、高さ)」の順だから、
点Aをもとにすると、点Bの位置は(横2cm、たて4cm、高さ2cm)と表せるよ。
点Cをもとにすると、点Dの位置はどのように表せるか。
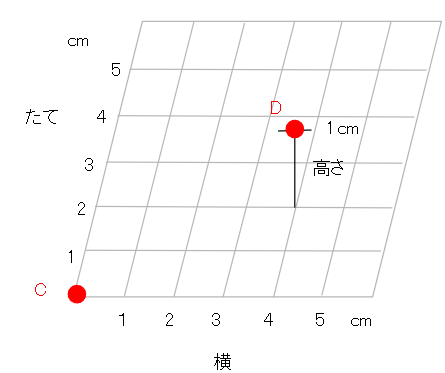
この問題では、「点Cから点Dまでどうやって行ったらいいか」を考えればいいね。
まず点Dの下の場所まで行こう。
横に4cm行って、たてに2cm行けば点Dの下の場所に行けるね。
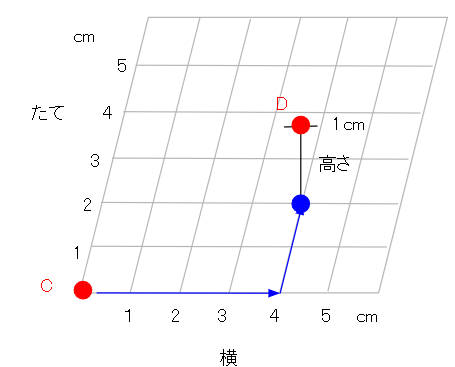
点Dの下の場所まで行ったら、あとは上に1cm行けばいいよね。
空間にある点の位置を表すときは、「(横、たて、高さ)」の順だから、
点Cをもとにすると、点Dの位置は(横4cm、たて2cm、高さ1cm)と表せるよ。
「位置の表し方」まとめ
「位置の表し方」まとめ
- 平面上の点を表すときは、(横、たて)の2つの長さの組で表せばよい。
- 空間上の点を表すときは、(横、たて、高さ)の3つの長さの組で表せばよい。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。



