「真分数・仮分数・帯分数」とは？分数の表し方をわかりやすく解説

小学校４年生の算数で学習する「分数の表し方」について、真分数・仮分数・帯分数とはなにか、仮分数を帯分数に直す方法、帯分数を仮分数に直す方法、帯分数を仮分数に直す裏ワザなどをわかりやすく解説するよ。

「真分数・仮分数・帯分数」とは？ 分数の表し方をわかりやすく解説のPDF（17枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• ３年生で学習した分数の復習
• 真分数とは
• 仮分数とは
• 帯分数とは
• 分数の表し方の練習問題
• 仮分数を帯分数に直す方法
• 帯分数を仮分数に直す方法
• まとめ

小学３年生のときに「分数」が登場したよね。
分数っていうのは、\(\frac{▢}{〇}\)のような形で表すことができる数のこと。

３年生で勉強した分数のふくしゅうをしておこう。

３年生のふくしゅう

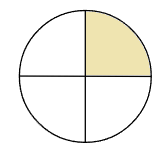
分数\(\frac{１}{４}\)だったら、
１このケーキを「４等分」した「１こぶん」になるよ。

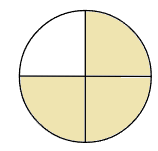
分数\(\frac{３}{４}\)だったら、
１このケーキを「４等分」した「３こぶん」になるよ。

今度はケーキではなく、テープの長さで考えてみよう。
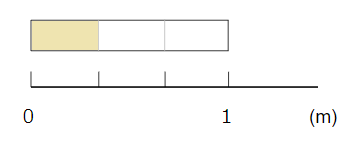
分数\(\frac{１}{３}\)だったら、
１ｍのテープを「３等分」した「１こぶん」になるよ。

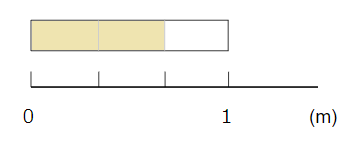
分数\(\frac{２}{３}\)だったら、
１ｍのテープを「３等分」した「２こぶん」になるよ。

分数とは何かを思い出せたかな？
実は分数は３つにわけることができるんだ。
じゅんばんにしょうかいしていくね。

真分数とは

まず１つ目の分数が「真分数しんぶんすう」だよ。
実は３年で勉強してきたのは「真分数」なんだ。

たろう

１より小さいってどういうことかな

真分数っていうのは、\(\frac{１}{４}\)のように、分子の方が分母より小さい分数のことだよね。

たとえばケーキで考えると、「ケーキ１こを４等分したうちの１こぶん」のことだよね。

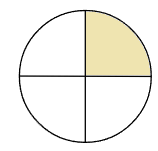
ケーキ１こをいくつかに分けたうちの何個かのことなんだから、分ける前のケーキ１こぶんよりは必ず小さくなるよね。
だから、真分数っていうのは必ず１より小さくなるんだ。

仮分数とは

４年生で初めて登場するのが「仮分数かぶんすう」だよ。

たろう

１と等しいか、１より大きいってどういうことかな

１と等しい仮分数とは　

たとえば\(\frac{４}{４}\)のような仮分数は、分子と分母が等しい分数だから、
ケーキで考えると、次のように「４等分したうちの４こぶん」なるよね。

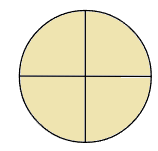
ケーキ１こを４等分したものが４つあったら、ちょうどもとのケーキ１こぶんになるよね。
だから、分子と分母が等しい仮分数は、「１と等しい」といえるんだ。

１より大きい仮分数とは

たとえば\(\frac{１１}{６}\)のような仮分数は、分子が分母より大きい分数だから、テープで考えると次のように「１ｍを６等分したうちの１１こぶん」になるよね。

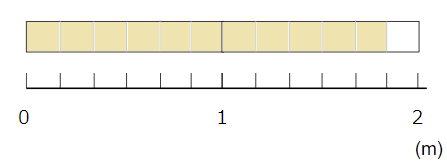
１ｍを６等分したものが６つあれば、ちょうどもとの１ｍになるよね。
でも分子は１１なので、さらにそれよりも多いということだね。
つまり、もとの大きさをこえてしまうんだね。だから、分子が分母より大きい仮分数は、「１より大きい」といえるんだ。

このように、仮分数は１と等しいか、１より大きい分数なんだね。

帯分数とは

帯分数たいぶんすうっていうのは、仮分数と仲良しなんだ。
さっきのテープの長さを見てみよう。

上のテープの長さは
\(\frac{１１}{６}\)と表すことができたよね。

ただ、この長さって、次のようにも言ってもいいよね。
「１ｍと\(\frac{５}{６}\)ｍ」

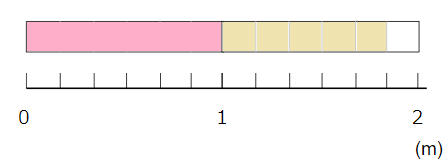
「１ｍと\(\frac{５}{６}\)ｍ」をあわせた長さは
「１\(\frac{５}{６}\)ｍ」と書いて、「１と６分の５メートル」と読むことができるよ。

これが帯分数だよ。
つまり、仮分数を違う書き方であらわしたものなんだね。

たろう

１より大きくなるってどういうことかな

帯分数って必ず、
〇\(\frac{５}{６}\)みたいな形になって、
〇には１より大きい数が入るんだ。

だから、帯分数は必ず１より大きくなるんだよ。
仮分数のときは、「１と等しい」ときもあったよね。でも帯分数の場合は、「整数と真分数の和で表される分数」なので、整数だけになることはないからね。

分数の表し方の練習問題

４年生で勉強する分数は次の３つだったね。

では、次の長さは、真分数・仮分数、帯分数のどれかな？

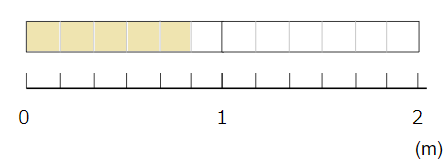
１より小さいから、真分数だよ。
１ｍを６等分した５こぶんだから、\(\frac{５}{６}\)とあらわせるね。

長さを仮分数・帯分数で表す問題

次のテープの長さを、仮分数・帯分数で表してみよう。

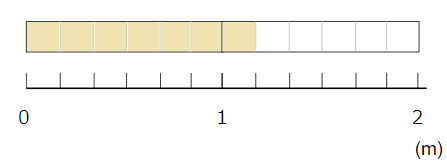
１ｍを６等分した７こぶんということは、１よりも大きいから仮分数と帯分数で表すことができるね。

仮分数で表すと、
１ｍを６等分した１こぶんが７つあるから、\(\frac{７}{６}\)とあらわせるね。

帯分数で表すと、
１ｍと\(\frac{１}{６}\)ｍだから、１\(\frac{１}{６}\)とあらわせるね。

仮分数を帯分数に直す方法

仮分数と帯分数は、同じ大きさの分数をちがう書き方であらわしたものだったよね。
だから、仮分数を帯分数の書き方に直したり、逆に帯分数を仮分数の書き方であらわしたりすることができるんだ。

仮分数と帯分数は同じ大きさの分数をあらわしているけれど、場合によって仮分数で表す方がわかりやすかったり、帯分数であらわしたほうがわかりやすかったりするよ。

たとえば、「ピザが\(\frac{２３}{６}\)枚あります。」と言われても、「・・・それって、どのくらいの量だろう？」と、いまひとつピンとこないよね。

でもこの「\(\frac{２３}{６}\)枚」を帯分数に直すと、
「４\(\frac{５}{６}\)枚」になるんだ。

これなら「ピザが４枚と\(\frac{５}{６}\)枚あるんだな」と、
どのくらいの量かがイメージしやすいよね。

それでは、仮分数を帯分数に直す方法を、問題をときながらみていこう。

仮分数を帯分数に直す練習問題①

\(\frac{１３}{６}\)っていうのは、
\(\frac{１}{６}\)が１３こあるっていう意味だよね。
テープの長さで考えると次のようになるよ。

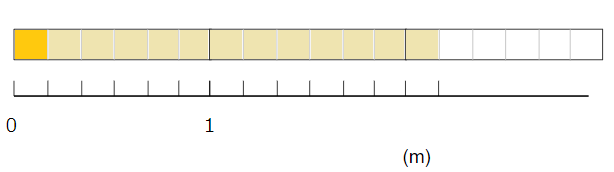
\(\frac{１}{６}\)が６こあると１ｍ
\(\frac{１}{６}\)が１２こあると２ｍ
になるから、

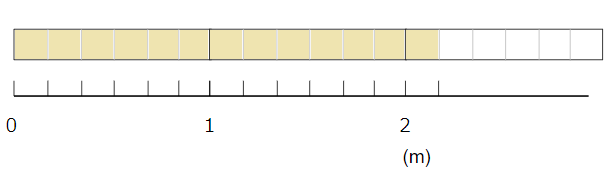
上の図を帯分数で表すと、
「２ｍと\(\frac{１}{６}\)ｍ」だから「２\(\frac{１}{６}\)ｍ」と求められるね。

割り算を使って仮分数を帯分数に直す方法

\(\frac{１３}{６}\)の中に\(\frac{６}{６}\)がいくつ入るか考えよう。
分子に注目すると、
１３の中に６がいくつ入るか考えればいいよ。

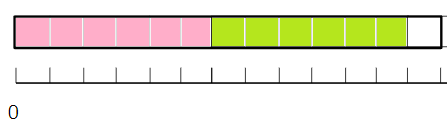
１３÷６＝２あまり１になるから、
\(\frac{６}{６}\)が２こ、\(\frac{１}{６}\)が１こだとわかるね。

\(\frac{６}{６}\)って「１」のことだから、
「２\(\frac{１}{６}\)ｍ」と求められるね。

仮分数を帯分数に直す練習問題②

\(\frac{８}{３}\)っていうのは、
\(\frac{１}{３}\)が８こあるっていう意味だよね。
テープの長さで考えると次のようになるよ。

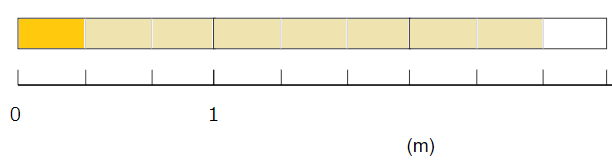
\(\frac{１}{３}\)が３こあると１ｍ
\(\frac{１}{３}\)が６こあると２ｍ
になるから、

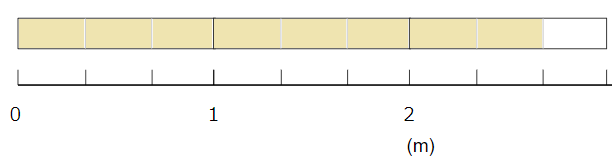
上の図を帯分数で表すと、
「２ｍと\(\frac{２}{３}\)ｍ」だから「２\(\frac{２}{３}\)ｍ」と求められるね。

割り算を使って仮分数を帯分数に直す方法

\(\frac{８}{３}\)の中に\(\frac{３}{３}\)がいくつ入るか考えよう。
分子に注目すると、
８の中に３がいくつ入るか考えればいいよ。

８÷３＝２あまり２になるから、
\(\frac{３}{３}\)が２こ、\(\frac{２}{３}\)が１こだとわかるね。

\(\frac{３}{３}\)って「１」のことだから、
「２\(\frac{２}{３}\)ｍ」と求められるね。

帯分数を仮分数に直す方法

今度はさっきの反対で、帯分数を仮分数に直すよ。

帯分数は、どのくらいの量かがわかりやすくなるんだけど、
帯分数のままだと計算しにくい時があるんだ。
そんなときは、帯分数を仮分数に直して計算するよ。

帯分数を仮分数に直す練習問題①

帯分数を仮分数に直すときは、帯分数の整数の部分「３」に注目しよう。

ポイントは、「３」が\(\frac{１}{２}\)なんこ分になるかを考えること

\(\frac{２}{２}\)が「１」と同じだから、「３」は\(\frac{１}{２}\)６こ分になるよね。

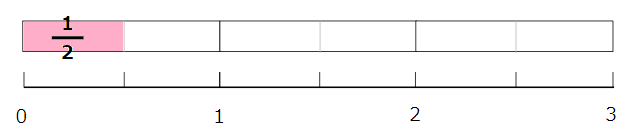
だから、３\(\frac{１}{２}\)っていうのは\(\frac{１}{２}\)が６こ分と\(\frac{１}{２}\)が１こ分

つまり\(\frac{１}{２}\)が（６＋１）＝７こ分になるよね。

仮分数にすると\(\frac{７}{２}\)と求められるよ。

帯分数を仮分数に直すときは、帯分数の整数の部分「２」に注目しよう。

ポイントは、「２」が\(\frac{１}{３}\)なんこ分になるかを考えること

\(\frac{３}{３}\)が「１」と同じだから、
「２」は\(\frac{１}{３}\)６こ分になるよね。

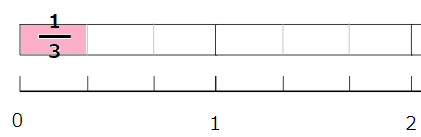
だから、２\(\frac{２}{３}\)っていうのは\(\frac{１}{３}\)が６こ分と\(\frac{２}{３}\)が１こ分

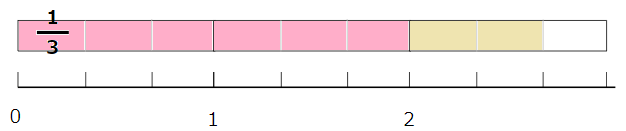
上の図を見ると
\(\frac{１}{３}\)が（６＋２）＝８こ分になるよね。

仮分数にすると\(\frac{８}{３}\)と求められるね。

帯分数を仮分数に直す「うらワザ」

今までやってきた方法だと、どうしても仮分数にするのに時間がかかっちゃうよね。
そこで、仮分数に直すワザをしょうかいするよ。

帯分数って、仮分数に直しても「分母は変らない」はずだよね。
ということは。あとは「分子の数がわかればOK」ということだよね。

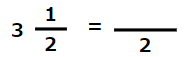
じつは仮分数の分子は、次のように
帯分数の「整数」×「分母」＋「分子」
で求めることができるんだ。

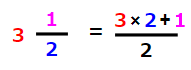
これを計算すると、
３\(\frac{１}{２}\)＝\(\frac{７}{２}\)になるよ。

「真分数・仮分数・帯分数とは（分数の表し方）」のまとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。