「面積」とは？単位と求め方をわかりやすく解説（広さの表し方）

小学校４年生の算数で学習する「面積」について、面積とはなにか、面積の単位（平方センチメートル）について、面積の求め方をわかりやすく解説するよ。

１平方センチメートル（１ｃｍ^２）をもとに、図形の面積を求める練習問題の考え方もくわしく紹介するよ。

「面積」とは？単位と求め方を わかりやすく解説（広さの表し方）のPDF（9枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 面積とは
• 平方センチメートル（ｃｍ^２）とは
• 面積を求める練習問題
• まとめ

面積とは

「面積」とは、図形の広さを数字で表したもののことだよ。

たとえば、下のように２つの図形があったとするよ。

この２つの図形の「どちらがどのくらい広いのか？」を数字で考えるときに、「面積」を使ってくらべるんだ。

くまごろう

もし「面積」がなかったら、「右の図形の方が大きいよ」「わたしは、左の方が少し大きいと思う」「ぼくは、右の方がかなり大きいと思う」というように、人によって意見がバラバラになってしまうよね。

「面積」という数字を使うことで「どちらがどのくらい広い（大きい）のか」を、みんなが同じように、調べることができるんだ。

「平方センチメートル（cm²)」とは

「平方へいほうセンチメートル（ｃｍ^２）」とは、「面積」の単位なんだ。

「長さ」に「ｃｍ（センチメートル）」という単位があったように、「面積」にも「平方センチメートル」という単位があるということだね。

平方センチメートルの記号は次のように書くよ。

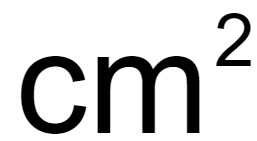
「ｃｍ」の右上に「２」がつくよ。
「ｃｍ」より少し小さめに「２」を書こう。
読み方は、面積の数字のあとに、「へいほうセンチメートル」をつけて読むよ。

「１平方センチメートル（１ｃｍ^２）」とは

「１ｃｍ^２（１平方センチメートル）」とは、「１辺が１ｃｍの正方形の面積」のことだよ。
図であらわすと、次のような大きさになるよ。

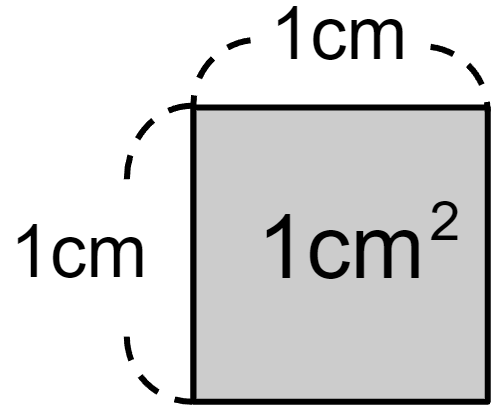
１ｃｍ^２（１平方センチメートル）は、だいたい指の「つめ」の広さとおなじくらいとイメージしておけばOKだよ。

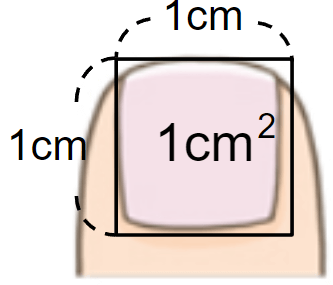
面積をあらわすときには、この「１ｃｍ^２（１平方センチメートル）」をもとに考えるんだ。

たとえば、５ｃｍ^２（５平方センチメートル）の面積だったら、「１ｃｍ^２（１平方センチメートル）が５こ分」の大きさということになるよ。

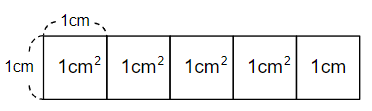
つまり、面積を求めるときには、「１ｃｍ^２（１平方センチメートル）がいくつあるか？」を考えればいいんだね。

面積を求める練習問題

では、じっさいに面積を求める問題にちょうせんしよう。

①と②の面積を求めなさい。

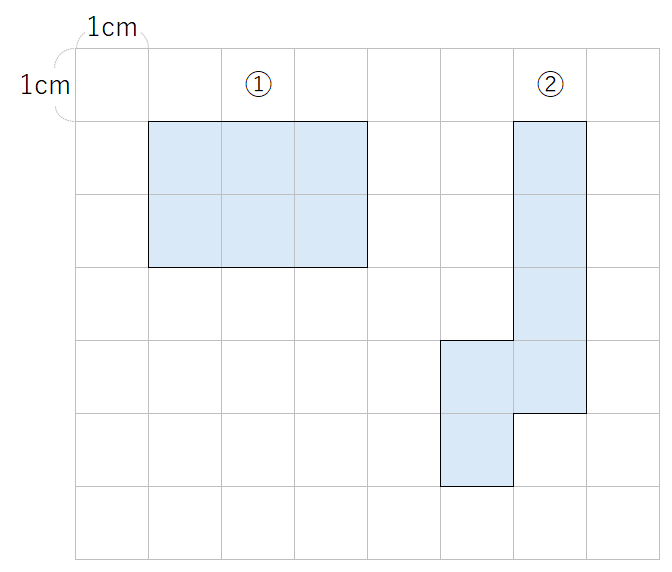
面積を求めるには、「１ｃｍ^２（１平方センチメートル）がいくつあるか？」を考えればいいんだったね。
だから、「１ｃｍ^２の正方形が何こあるか」を数えればOKだよ。

➀も➁も、どちらとも１ｃｍ^２の正方形が６こあるから、「６ｃｍ^２」と求めることができるね。

たろう

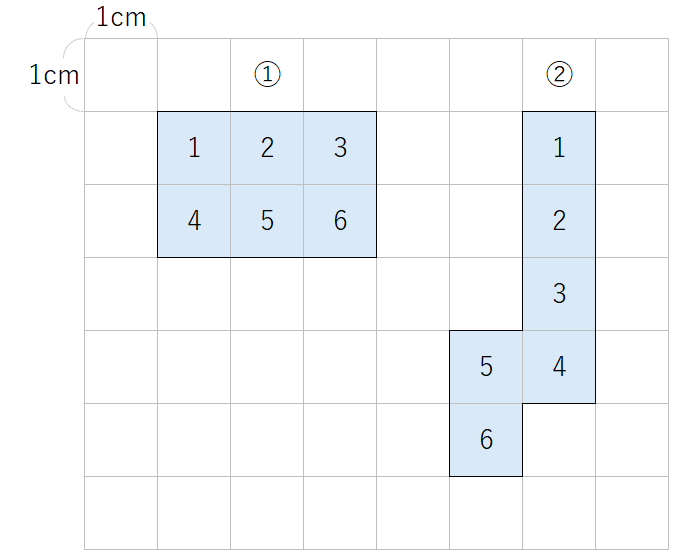
読み方は「６平方センチメートル」だね。

①と②の面積を求めよう。

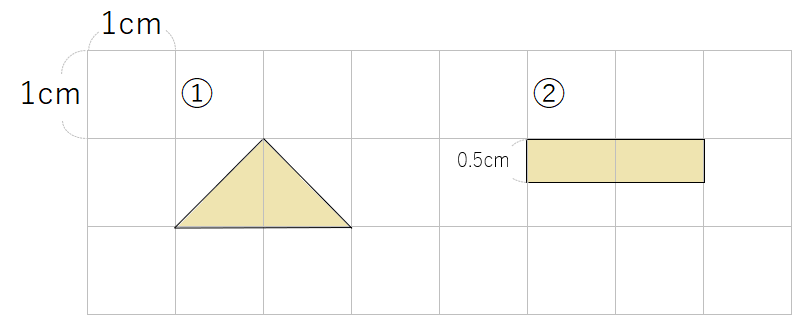
「あれ？？」とフシギに思った人もいるかもしれないね。

面積を求めるには、「１ｃｍ^２の正方形何こあるか」を考えればよかったのだけれど、この問題の図形には「正方形」が１つもないから、こまってしまうよね。

こういうときは、図形を切ったり動かしたりして、正方形を作ってしまえばいいんだ。

例えば、①の三角形だったら、水色の部分を下のように動かしてみよう。

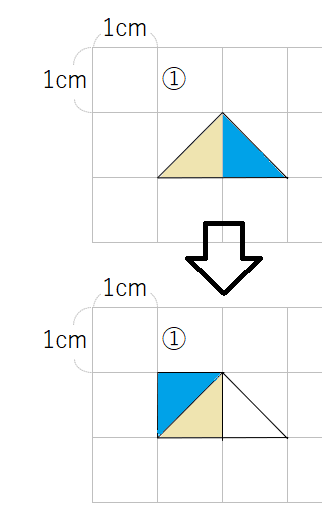
正方形を作ることができたね。
こうすると、１ｃｍ^２の正方形１つ分と同じになるから、面積は１ｃｍ^２だよ。

では今度は②を考えてみよう。水色の部分を下のように動かしてみるよ。

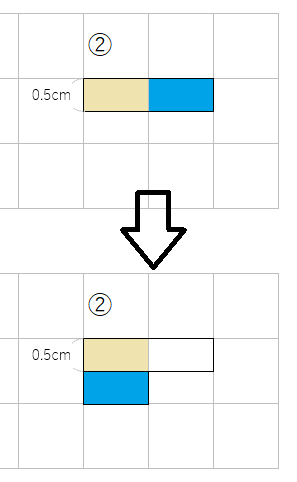
今度も正方形を作ることができたね。
こうすると、１ｃｍ^２の正方形１つ分と同じになるから、面積は１ｃｍ^２だね。

次の平行四辺形の面積を求めなさい。

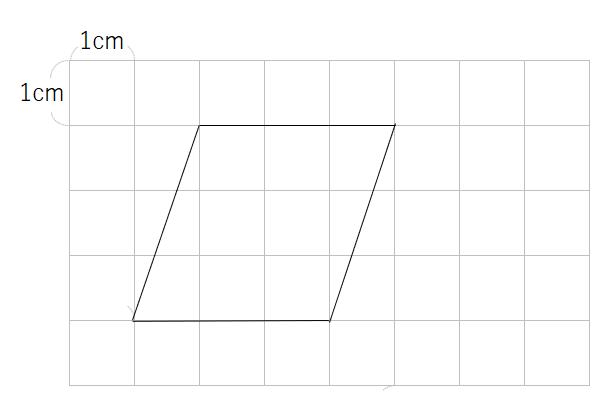
今度は、正方形の部分もあるけれど、そうでない部分もあるね。

まずは、１ｃｍ^２の正方形の部分から考えよう。

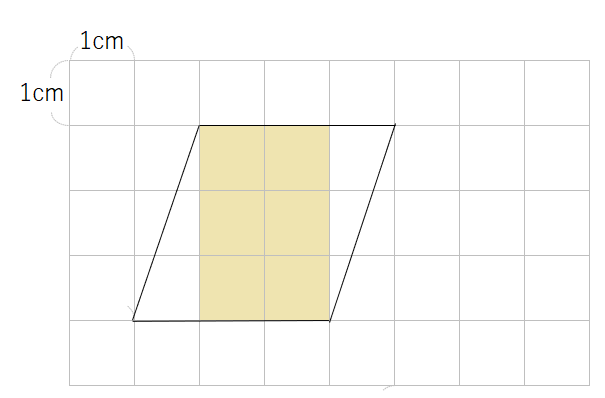
１ｃｍ^２の正方形は６つあるね。

次に、はんぱな形の面積を求めよう。

水色の部分を合体させたら、１ｃｍ^２の正方形になるよね。

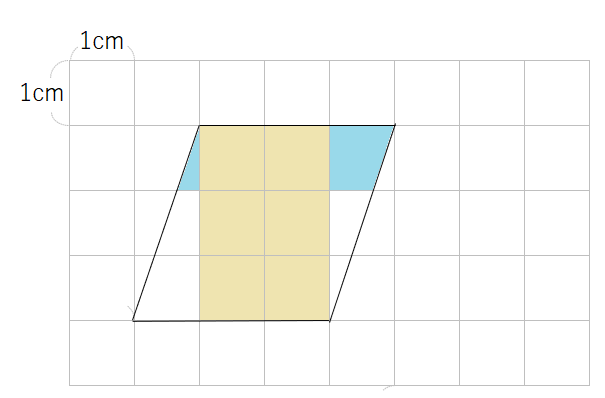
同じように、緑の部分を合体させても、１ｃｍ^２の正方形になるよね。

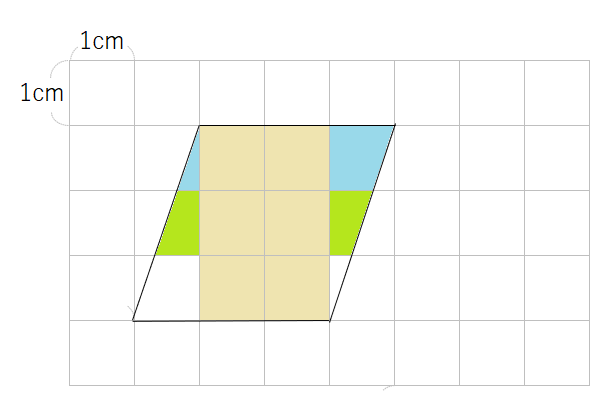
最後に、オレンジの部分を合体させても、１ｃｍ^２の正方形になるよね。

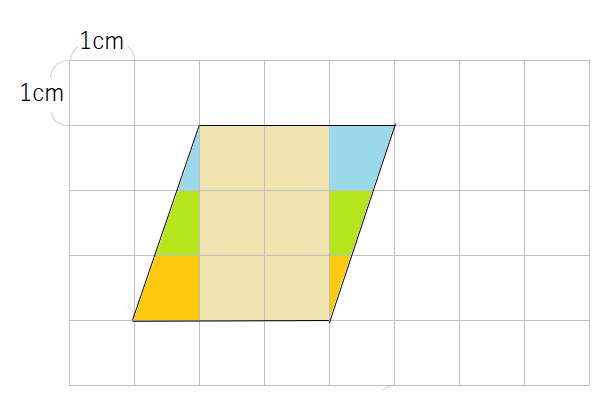
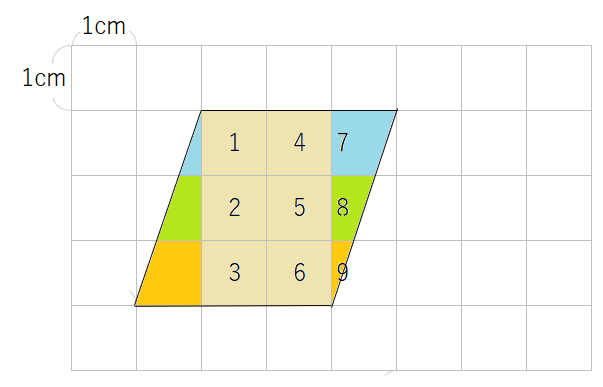
ということは、１ｃｍ^２の正方形が６つと、合体してできた１ｃｍ^２の正方形が３つということだね。

だから、この平行四辺形の面積は９ｃｍ^２と求めることができるよ。

面積の単位と求め方（広さの表し方）まとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。