「変わり方調べ」ともなって変わる量をわかりやすく(練習問題)
小学校4年生の算数で学習する「変わり方調べ」について、「ともなって変わる量」とは何か、表を見て変わり方を調べる考え方、変わり方の関係を式に表す方法、正三角形や正方形の変わり方調べの練習問題の解き方をわかりやすく解説するよ。
「ともなって変わる量」とは
「ともなって変わる」とは、2つのものの、かた方が変わると、もう一方も変わるということだよ。
「ともなって」とは、「一緒に」という意味なんだ。だから、「一緒に変わる(かた方が変わると、もう一方も変わる)」ということだね。
「ともなって変わる量」には、たとえば次のようなものがあるよ。
ともなって変わる量の例
- 「水そうにいれる水の量」と「深さ」
水そうにいれる水の量が増えたりへったりすれば、深さもあさくなったり深くなったりするよね。 - 「長方形の長さ」と「面積」
長方形の長さ(辺の長さ)がみじかくなったり長くなれば、面積も小さくなったり大きくなったりするよね。
それでは、「ともなって変わる量」がじっさいにどんなふうに変わるのか見てみよう。
たとえば1辺が1cmの「正三角形の数」と「周りの長さ」について考えてみるよ。
正三角形が1つのとき、周りの長さは1cmが3つ分だから「3cm」になるよね。
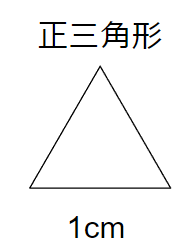
じゃあ、次のように正三角形が2つになったら、周りの長さはどうなるかな?
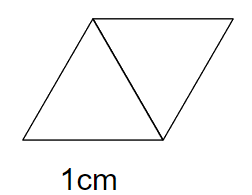
正三角形が2つの場合、周りの長さって赤線のところになるよね。
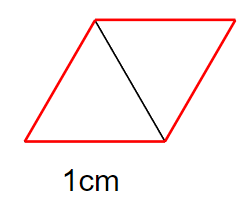
1cmが4つあるから「4cm」になるね。
じゃあ、正三角形が3こ、4こ・・・とふえていくと、周りの長さはどうなるかな?
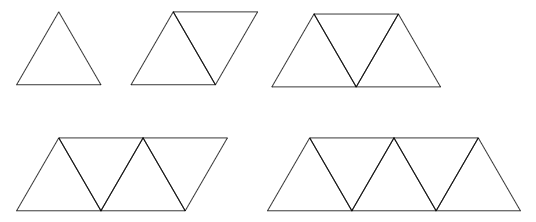
「変わり方調べ」表をたてや横に見て関係を見つけよう
1辺が1cmの「正三角形の数」と「周りの長さ」の関係を、表にまとめてみるよ。
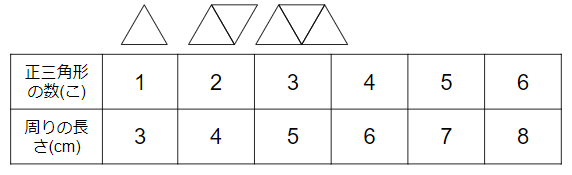
では、正三角形の数と周りの長さにはどんな関係があるか見ていこう。
表の関係を見るには、「たて」で見る方法と「横」で見る方法があるんだ。
表をたてに見る
表をたてに見ると、正三角形の数に「2」をたすと、周りの長さになっていることがわかるね。
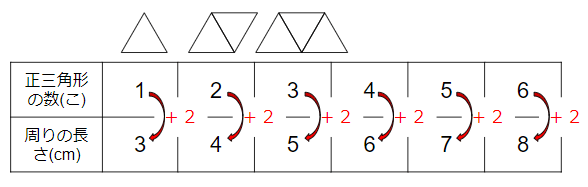
表を横に見る
表を横に見ると、正三角形の数が1こふえると、周りの長さも1cm長くなっていることがわかるね。
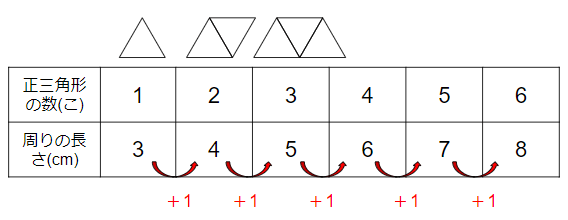
「変わり方調べ」関係を式に表そう
ともなって変わる量の関係を式にするコツは、「その関係を言葉にしてみる」こと。
正三角形の数と周りの長さの関係の表をたてに見たとき、「正三角形の数に「2」をたすと、周りの長さになっていたよね。
この関係を言葉にすると、
「正三角形の数」に2をたすと「周りの長さ」になる
だよね。

言葉にしたら、「2つのもの」をそれぞれ▢や〇におきかえてみるよ。
たとえば、「正三角形の数」を▢にして、「周りの長さ」を〇にすると、
▢+2=〇
という式で表すことができるね。
関係を式で表すといいこと
どうしてわざわざ、関係を式にするのか?というと、「ともなって変わる量」を式で表すと、いいことがあるんだ。
それは、「数が大きくなっても、すぐに答えを求められること」。
たとえば、もし式がなかったら、「正三角形が100このとき、周りの長さは何cmになるか?」と聞かれたら、じっさいに正三角形を100こも描いてみるのは大変だよね。
でも、式があれば、▢や〇の中に数字を入れるだけで、答えをもとめることができるんだ。
さっき作った「▢+2=〇」の▢に、100をいれてみよう。
そうすると、
100+2=102になって、
周りの長さは102cmとすぐに求めることができるね。
「変わり方調べ」練習問題
「変わり方調べ」では、どんな問題が出るのか確認をしてみよう。
1辺が1cmの正方形を、下の図のように1だん、2だん・・・とならべていきます。次の問題に答えなさい。
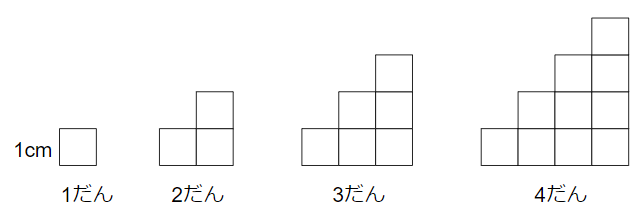
(1)「だんの数」と「周りの長さ」の関係を表で表しなさい。
(2)「だんの数」と「周りの長さ」の関係を式で表しなさい。
(3)だんの数が50このとき、周りの長さは何cmですか。
(4)周りの長さが80cmになるときは何だんですか。
(1)「だんの数」と「周りの長さ」の関係を表で表そう
1だんのときは、1cmが4辺ぶんあるので、周りの長さは「4cm」になるよね。
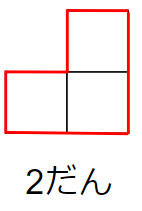
2だんのときは、赤線の部分が周りの長さになるから「8cm」になるよね。
3だん、4だんのときも、周りの長さを求めて、表にすると、次のようになるよ。
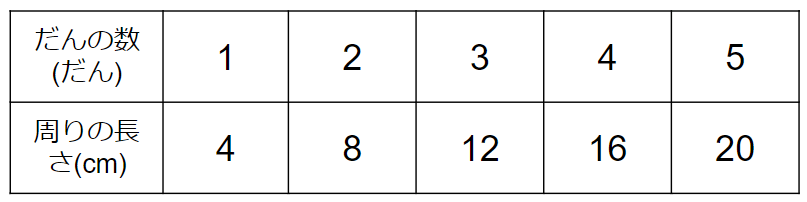
(2)「だんの数」と「周りの長さ」の関係を式で表そう
表をたてに見ると、「だんの数」を4倍にすると「周りの長さ」になっていることがわかるよね。
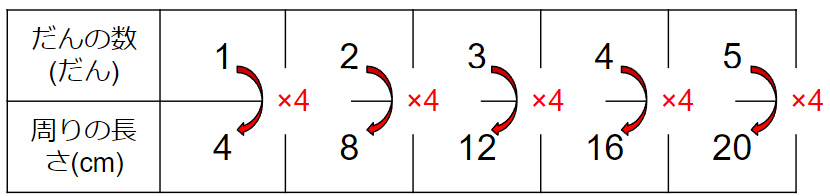
「だんの数」を▢、「周りの長さ」を〇としたら、
▢×4=〇
という式で表すことができるね。
(3)だんの数が50このとき、周りの長さは何cmか求めよう
「だんの数」を▢としたから、
▢×4=〇の「▢」に50をいれてみよう。
そうすると
50×4=200になって、
周りの長さが200cmとわかるよ。
(4)周りの長さが80cmになるときは何だんか求めよう
「周りの長さ」を〇としたから、
▢×4=〇の「〇」に80をいれてみよう。
そうすると
▢×4=80になるよ。
▢に4をかけると80になるから、
▢は20とわかるね。
▢は「だんの数」だったから、
周りの長さが80cmになるのは、「20だん」のときと求めることができるよ。
1辺が1cmの正三角形を、下の図のように1だん、2だん・・・とならべていきます。次の問題に答えなさい。
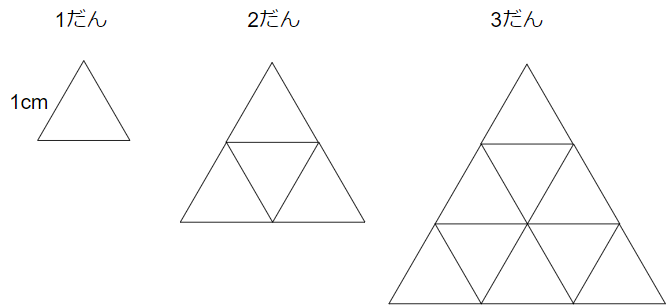
(1)「だんの数」と「周りの長さ」の関係を表で表しなさい。
(2)「だんの数」と「周りの長さ」の関係を式で表しなさい。
(3)だんの数が50このとき、周りの長さは何cmですか。
(4)周りの長さが90cmになるときは何だんですか。
(5)だんの数が2倍、3倍になると、周りの長さはどのようになっているか。
(1)「だんの数」と「周りの長さ」の関係を表で表そう
1だんのときは、1cmが3辺ぶんあるので、周りの長さは「3cm」になるよね。
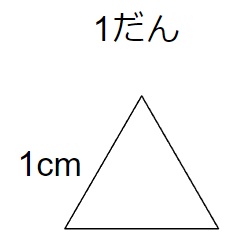
2だんのときは、赤線の部分が周りの長さになるから「6cm」になるよね。
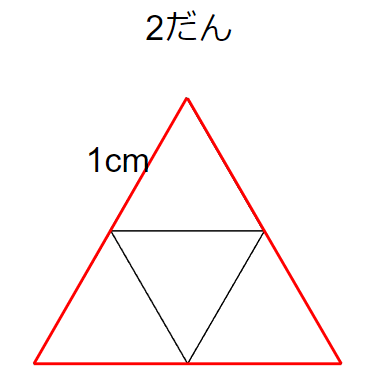
3だんのときは、赤線の部分が周りの長さになるから「9cm」になるよね。
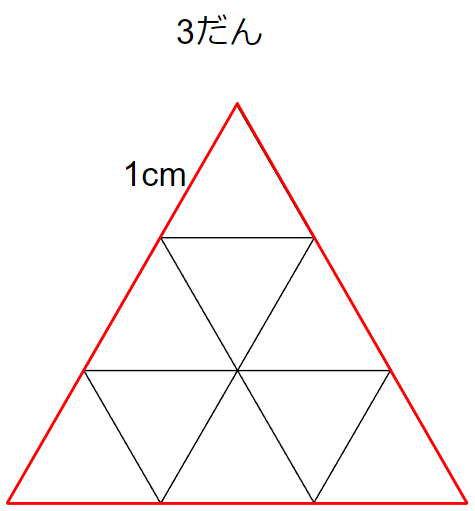
ここまでを表にすると、次のようになるよね。
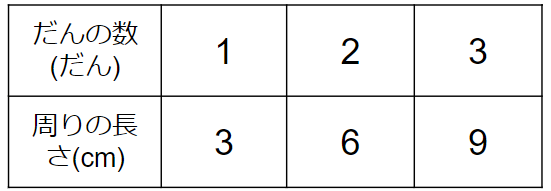
(2)「だんの数」と「周りの長さ」の関係を式で表そう
表をたてに見ると、「だんの数」を3倍にすると「周りの長さ」になっていることがわかるよね。
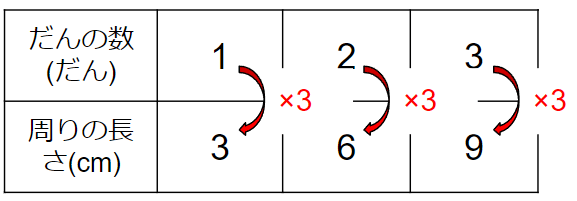
「だんの数」を▢、「周りの長さ」を〇としたら、
▢×3=〇
という式で表すことができるね。
(3)だんの数が50このとき、周りの長さは何cmか求めよう
「だんの数」を▢としたから、
▢×3=〇の「▢」に50をいれてみよう。
そうすると
50×3=150になって、
周りの長さが150cmとわかるよ。
(4)周りの長さが90cmになるときは何だんか求めよう
「周りの長さ」を〇としたから、
▢×3=〇の「〇」に90をいれてみよう。
そうすると
▢×3=90になるよ。
▢に3をかけると90になるから、
▢は30とわかるね。
▢は「だんの数」だったから、
周りの長さが90cmになるのは、「30だん」のときと求めることができるよ。
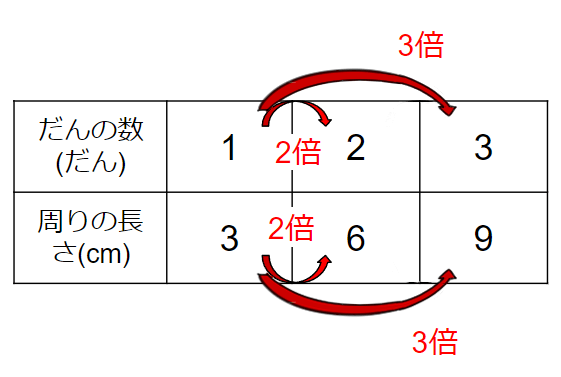
(5)だんの数が2倍、3倍になると、周りの長さはどのようになっているか求めよう
表を見てみると、だんの数が1から2で「2倍」になると、周りの長さも3から6で「2倍」、だんの数が1から3で「3倍」になると、周りの長さも3から9で「3倍」になっていることがわかるよ。
ちなみにこの関係のことを「比例」というよ。
「比例」は、小学5年生の算数で登場するよ。
「変わり方調べ(ともなって変わる量)」まとめ
変わり方調べ「ともなって変わる量」のまとめ
- 「ともなって変わる」とは、2つのものの、かた方が変わると、もう一方も変わること。
- 「ともなって変わる量」を表で表せたら、表をたてに見たり、表を横で見て変わり方を調べよう。
- 「ともなって変わる量」の関係は、式で表すこともできる。
式で表すことで、数が大きくなった時にすぐに答えを求められるようになる。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


