3けたのわり算の工夫・百の位に商がたたないわり算の筆算のやり方
小学校4年生の算数で学習する「3けたのわり算の筆算の工夫」のやり方やポイントと、「百の位に商がたたない場合のわり算の筆算のやり方」をわかりやすく解説するよ。
わり算の筆算の工夫をつかって、筆算をはやくとけるようにしよう。
3けたの割り算の筆算を速くする方法
3けたのわり算の筆算って、答えが求まるまでにすごくたくさんノートを使うよね。
たとえば、「619÷3」の筆算の場合をみてみよう。
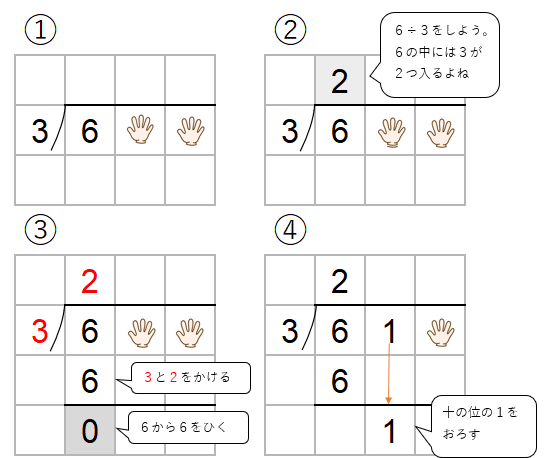
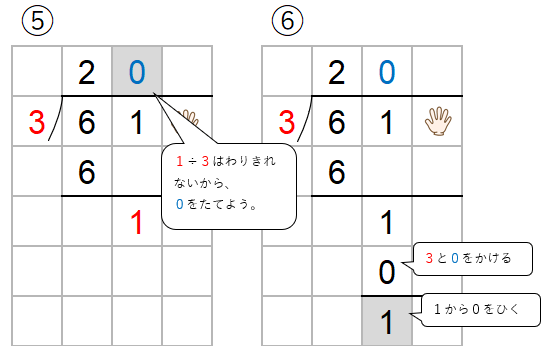
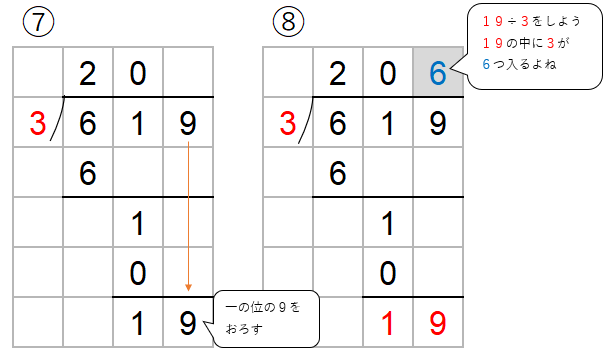
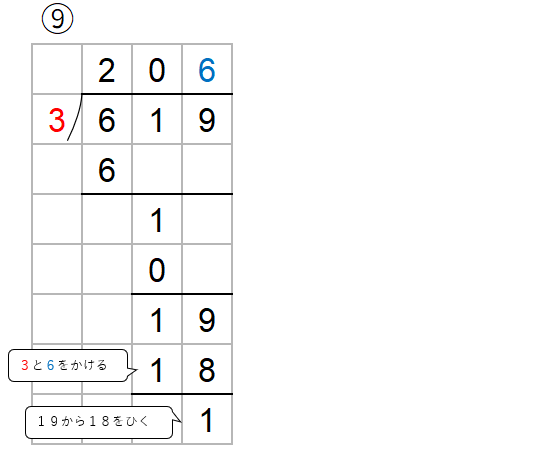
619÷3=206あまり1と求めることができたね。
ただ、ノートは8行も使ってしまったよね。
割り算の筆算の工夫
わり算の筆算のどこを工夫するかというと、ズバリ「商に0がたつところ」だよ。
さっきの筆算の手順⑥を見てみよう。
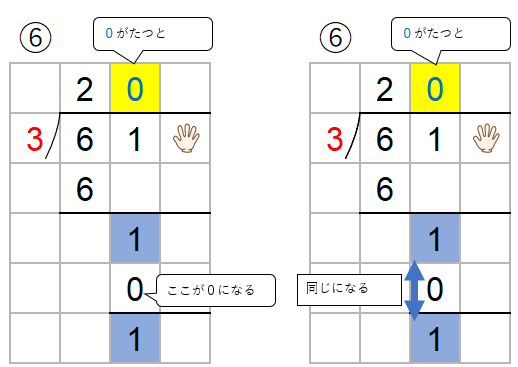
もし、商に0がたつと、たてた数0とわる数のかけ算は必ず0になるよね。
ということは、もし商に0がたつと、0をひくことになるから、上と下の数字「1」は同じになるよね。
だから、商に0がたったときは次のように筆算の一部をしょうりゃくすることができるんだ。
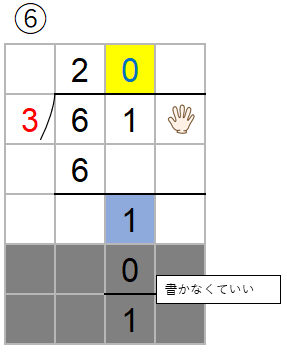
2行しょうりゃくすることができたから、次のような計算になるよ。
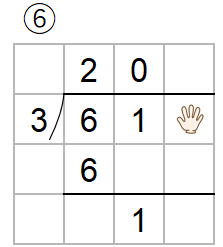
1÷3は計算できないなと思ったら、十の位に0をたてて、下のように一の位の「9」をおろせばOK。
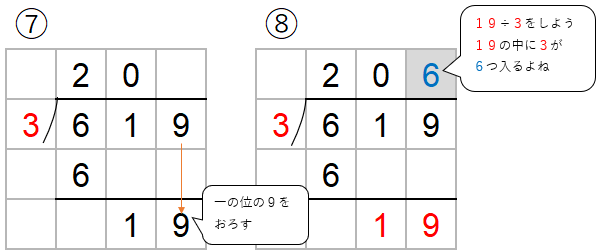
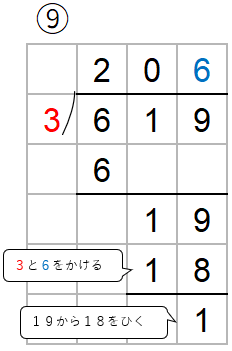
工夫しないときは8行も使ってしまったけれど、工夫すると6行で求めることができたね。
工夫するポイント
- 商に「0」がたつとき、
商とわる数のかけ算の答えは0になるから、書かなくてもいい。
百の位に商がたたないわり算の筆算
「百の位に商がたたないわり算」とはどういうことかというと、「百の位に0がたつ」ということだよ。
じっさいに問題を見ていこう。
256÷4を筆算を使って計算しなさい。
わり算の筆算は次のようになるよね。
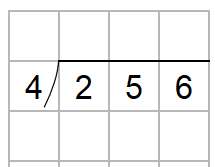
まずは、百の位だけをわり算するよ。
なので、十の位と一の位は「ちょっとまっていてね」と、手でかくしてしまおう。
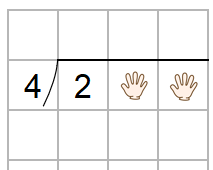
十の位と一の位をかくすと、2÷4になるね。
ステップ1:百の位をわる
百の位の「2」を「4」でわるよ。
2の中に4がいくつ入るか考えると…「あれ?入らないよ」ってなるよね。
そういう、わりきれないときは「0」をたてるんだったよね。
だから、百の位の屋根の上に「0」を書こう。
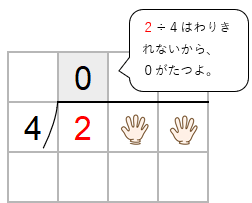
ステップ2:たてた数とわる数をかける
次に、わる数4と百の位の上にたてた0をかけた数を2の下に書くよ。
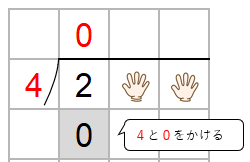
ステップ3:百の位でひき算をする
2から0をひくよ。
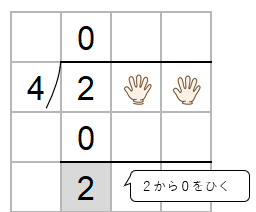
とやってもいいんだけど、商に「0」がたつときは工夫ができたよね。
ステップ2~5をしょうりゃくする
2÷4はわりきれないから、百の位に「0」がたって、
かくしていた十の位の「5」を見えるようにしよう。
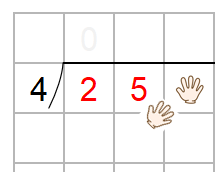
こうすることで、ステップ2~5をしょうりゃくすることができるんだ。
商に「0」がたつときはしょうりゃくできると覚えておこう。
ステップ1:十の位をわる
25の中に4がいくつ入るか考えると4つだね。
だから、十の位に「4」を書くよ。
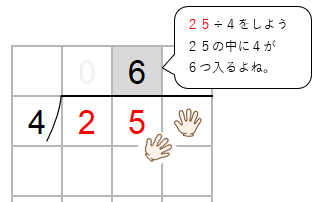
ステップ2:たてた数とわる数をかける
次に、わる数4と十の位の上にたてた6をかけた数を25の下に書くよ。
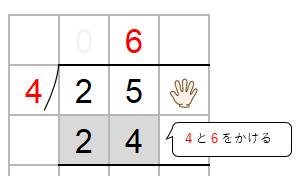
ステップ3:ひき算をする
25から24をひくよ。
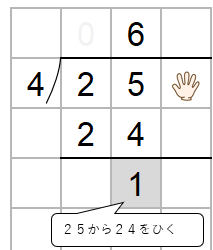
ステップ4:いちどチェックしよう
ここでチェックすることがあったね。
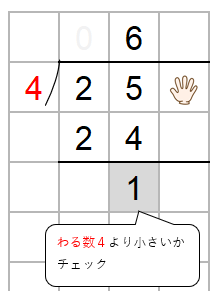
ひき算した数がわる数4より小さいかをかくにんしよう。
1は4より小さいからOKだね。
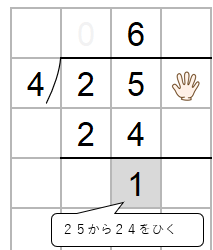
ステップ5:一の位をおろす
十の位のわり算はもうできることがないね。
だから、ここで「かくしていた一の位」の出番だよ。
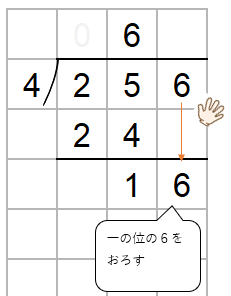
かくしていた一の位の「6」を下におろそう。
このステップを「一の位とわる数」でくりかえすよ。
ステップ1:一の位をわる
16の中に4がいくつ入るか考えると4つだね。
だから、一の位に「4」を書こう。
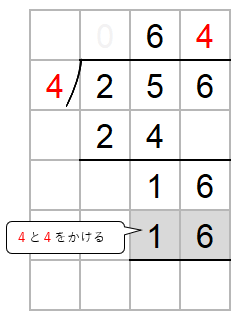
ステップ2:たてた数とわる数をかける
次に、わる数4と一の位の上にたてた4をかけた数を16の下に書くよ。
ステップ3:ひき算をする
16から16をひくよ。
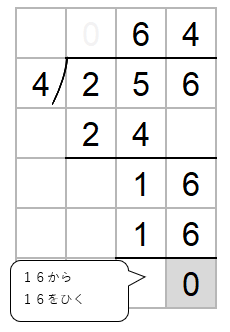
ステップ4:いちどチェックしよう
ここでチェックすることがあったね。
ひき算した数がわる数4より小さいかをかくにんしよう。
0は4より小さいからOKだね。
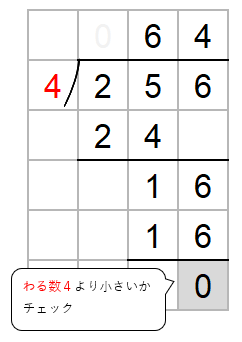
ステップ5は「おろす」なんだけれど、3けたのわり算なので、これ以上おろせるものは残っていないよね。
だから、これで256÷4の筆算は終わりになるよ。
屋根の上に乗っている64がわり算の答え
ここまでできたら、屋根の上に乗っている数字をみてみよう。
「064」なんだけど、0は考えなくていいよね。
だから
256÷4=64と求めることができたね。
百の位に商がたたないわり算の筆算の流れ
百の位に商がたたないわり算の筆算をまとめると次のような流れで計算を進めていくよ。
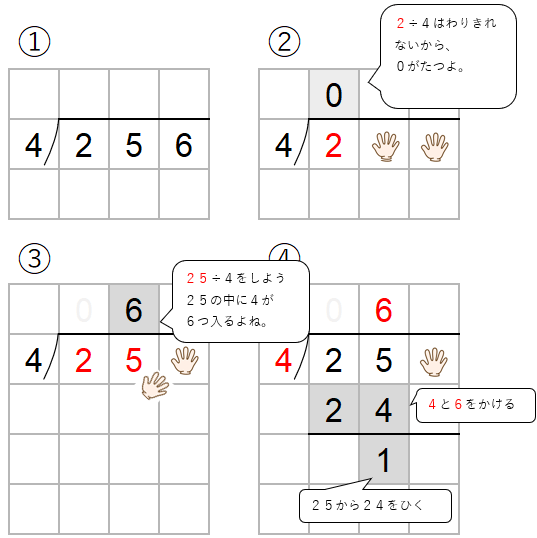
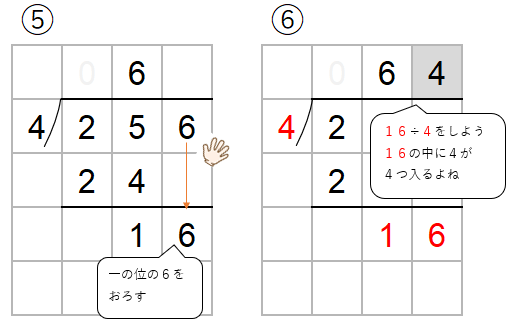
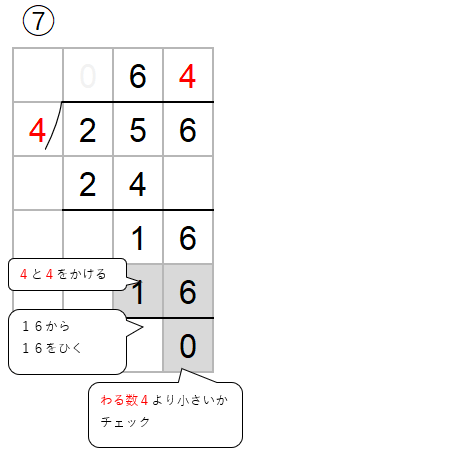
百の位に商がたたないわり算の筆算の流れ
- 「百の位に商がたたない」とは「百の位に0がたつ」と同じで、
わりきれないということ。 - 百の位に商がたたない場合は、十の位の数まで考えて、わりきれるかかくにんしよう。
ちなみに、十の位の数まで考えても、わりきれない場合は、「一の位の数」まで考えよう。
百の位に商がたたないわり算の筆算の練習
125÷4を筆算で計算しなさい。
今までと同じように計算していくと次のようになるよ。
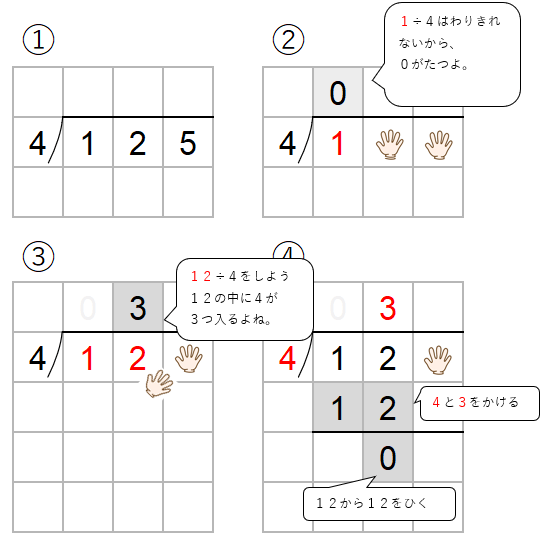
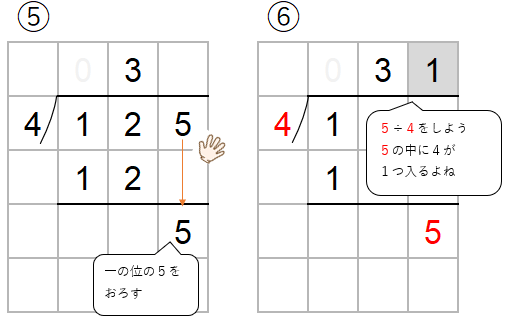
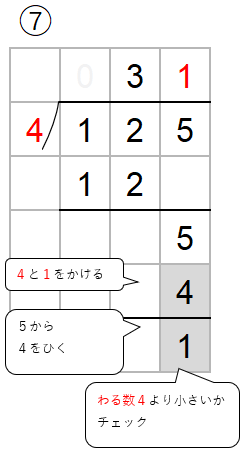
125÷4=31あまり1と求めることができるよ。
百の位に商がたたない筆算
どういうわり算のときに、百の位に商がたたないか考えてみよう。
今までの筆算をふりかえると次のようになるよ。
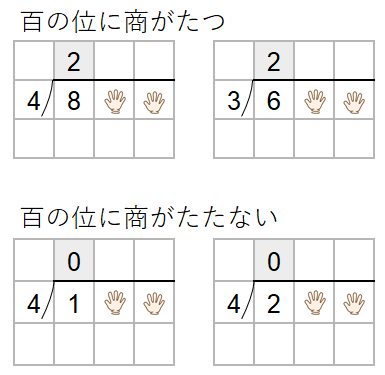
なんとなくわかると思うけど、「わられる数の百の位より、わる数の方が大きい」と、百の位に商がたたないんだね。
これはあたりまえだよね。
だって、わる数の方が大きいとわりきれないもんね。
百の位に商がたたない筆算
- わられる数の百の位より、わる数の方が大きいと、百の位に商がたたない。
- 下の図でいうと、〇より△の方が大きいと、百の位には商がたたない。
「3けたのわり算の工夫・百の位に商がたたないわり算の筆算」まとめ
「3けたのわり算の工夫・百の位に商がたたないわり算の筆算」まとめ
- 商に「0」がたつと、筆算の計算をしょうりゃくすることができる。
- 百の位に商がたたないときは、かくしていた十の位をみえるようにして考える。
- わられる数の百の位より、わる数の方が大きいと、百の位に商がたたない。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。