「分母がちがう分数の大きさ」分数の大きさ比べをわかりやすく解説

分数の大きさの比べ方は？分母がちがう分数の大きさはどうやって比べるのか？「分母がちがう分数の大きさ」の比べかたや、分母がちがっても同じ大きさの分数とはどんなものかなどをわかりやすく解説するよ。

「分母がちがう分数の大きさ」 分数の大きさ比べをわかりやすく解説のPDF（9枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

目次

• 分数の大きさをくらべてみよう
• 分母がちがっても大きさが等しい分数
• 「分数の大きさくらべ」の練習問題
• まとめ

分数の大きさをくらべてみよう

前回、分数の表し方について勉強したよね。
分数の表し方では、「真分数」や「仮分数」や「帯分数」という言葉が登場したと思うけれど、今回の「分数の大きさくらべ」では、真分数で考えていくよ。

真分数というのは、\(\frac{１}{４}\)、\(\frac{４}{５}\)、\(\frac{１}{７}\)、\(\frac{９}{１０}\)のような、分子が分母より小さい分数のことだったよね。

４年生の算数では、分数の大小をくらべることができるパターンは２つあるよ。

じゅんばんにしょうかいしていくね。

分母が同じ分数の大きさをくらべよう

分数の大きさをくらべられるパターン１つ目の
「分母が同じ分数」をみていこう。

れいだい①

\(\frac{１}{３}\)と\(\frac{２}{３}\)って、
どちらとも分母が「３」で同じだよね。

じゃあ、\(\frac{１}{３}\)と\(\frac{２}{３}\)ってどっちが大きいかな？
\(\frac{１}{３}\)と\(\frac{２}{３}\)を図で表してみよう。

• \(\frac{１}{３}\)は、３等分した１つ分

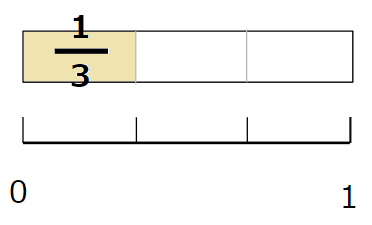
• \(\frac{２}{３}\)は、３等分した２つ分

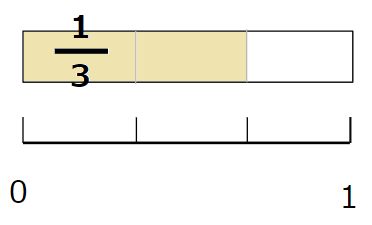
上の図からもわかると思うけれど、
\(\frac{２}{３}\)の方が\(\frac{１}{３}\)より大きいよね。

れいだい②

\(\frac{１}{６}\)と\(\frac{５}{６}\)って
どちらも分母が「６」で同じだよね。

じゃあ、\(\frac{１}{６}\)と\(\frac{５}{６}\)ってどっちが大きいかな？
\(\frac{１}{６}\)と\(\frac{５}{６}\)を図で表してみよう。

• \(\frac{１}{６}\)は、６等分した１つ分

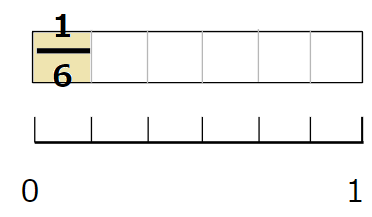
• \(\frac{５}{６}\)は、６等分した５つ分

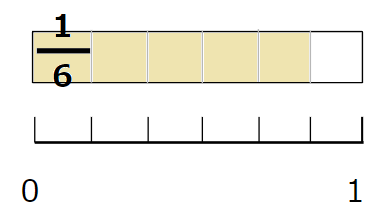
上の図からもわかると思うけど、
\(\frac{５}{６}\)の方が\(\frac{１}{６}\)より大きいよね。

分母が同じ分数のくらべかた

図であらわしてみると、とても簡単だね。
「分母が同じ分数の場合は、分子が大きい分数の方が大きくなる」んだ。

でもこれって当たり前だよね。
分母が同じ分数は、全体を同じ数字で等分（分けた）したもので、分子の数は「それがいくつあるか」をあらわすものだよね。

分子の数が大きくなればなるほど、等分したものがたくさんあることになるから、その分数の方が大きくなるよね。

分子が同じ分数の大きさを比べよう

分数の大きさをくらべられるパターン２つ目の
「分子が同じ分数」をみていこう。
分子が同じであればいいので、「分母がちがう分数の大きさ」でもくらべられるということだね。

れいだい①

たとえば、\(\frac{１}{３}\)と\(\frac{１}{６}\)ってどっちが大きいかな？
分母はちがうけれど、どちらとも分子が「１」で同じになっているね。

• \(\frac{１}{３}\)は、３等分した１つ分

• \(\frac{１}{６}\)は、６等分した１つ分

どちらも「１つ分」なんだけれど、
\(\frac{１}{６}\)の方が、「６等分」されているから
「１つ分」は小さくなっているよね。

れいだい②

じゃあ、\(\frac{２}{５}\)と\(\frac{２}{９}\)ってどっちが大きいかな？
どちらとも分子が「２」で同じになっているね。

• \(\frac{２}{５}\)は、５等分した２つ分

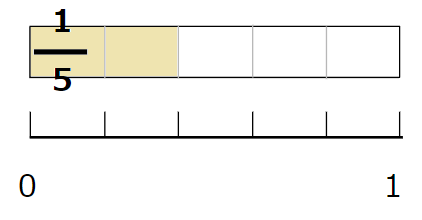
• \(\frac{２}{９}\)は、９等分した２つ分

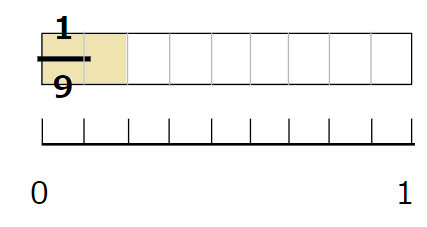
どちらも「２つ分」なんだけれど、
\(\frac{２}{９}\)の方が、「９等分」されているから
「２つ分」は小さくなっているよね。

分子が同じ分数のくらべかた

「分子が同じ分数の場合は、分母が大きい分数の方が小さくなる」んだ。
だって、分母が大きいということは、それだけ「小さく等分している」ということになるからね。
同じものをわけるとき、たくさんにわけたほうが１つあたりの大きさは小さくなるよね。

分子は、「〇つ分」をあらわすものだよね。そして分母は、「いくつにわけているか」だよね。
「〇つ分」が同じなのであれば、たくさんにわけられているもののほうが、その大きさは小さくなるね。

分母がちがっても大きさが等しい分数

これまで、「どちらの分数の方が大きいか」の考え方を勉強してきたよね。

今度は、\(\frac{３}{６}\)と\(\frac{１}{２}\)のように、「分母も分子も数字がちがうのに大きさが等しくなる分数」について説明していくよ。

\(\frac{３}{６}\)と\(\frac{１}{２}\)を図であらわしてみよう。２つの大きさは同じだということがわかるかな？

\(\frac{１}{２}\)とは、２等分した「１つ分」　

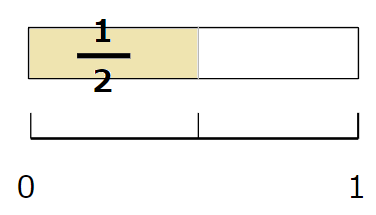
\(\frac{３}{６}\)とは、６等分した「３つ分」　

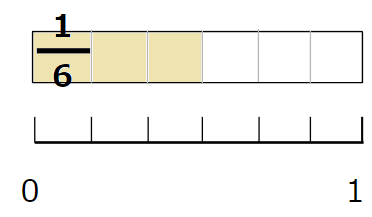
２等分した「１つ分」って、分数にすると\(\frac{１}{２}\)になるよね。
６等分した「３つ分」って、分数にすると\(\frac{３}{６}\)になるよね。

図であらわすと、どちらも「ちょうど半分」で同じ大きさを表しているから、\(\frac{１}{２}\)と\(\frac{３}{６}\)は同じ大きさなんだ。

ほかにも、下の分数も同じ大きさを表しているよ。

\(\frac{１}{２}\)と同じ大きさの分数

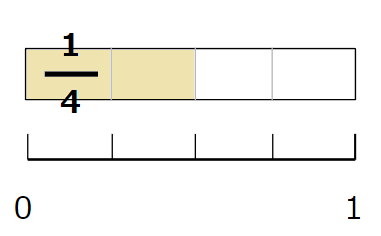
• \(\frac{２}{４}\)

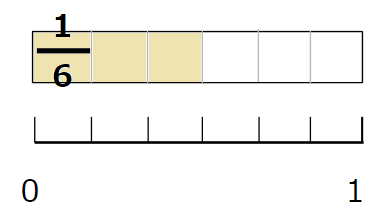
• \(\frac{３}{６}\)

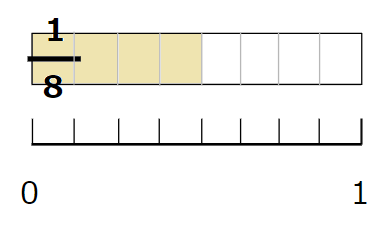
• \(\frac{４}{８}\)

「分数の大きさくらべ」の練習問題

どちらとも分母が「４」で同じだよね。
分母が同じときは、分子が大きい方が、分数も大きくなるから、
\(\frac{３}{４}\)の方が大きいよ。

不等号で表すと\(\frac{１}{４}\)＜\(\frac{３}{４}\)になるね。

では、次の問題にちょうせんしてみよう。

どちらとも分子が「３」で同じだよね。
分子が同じときは、分母が大きい方が、分数は小さくなるから
\(\frac{３}{７}\)の方が小さいよ。

不等号で表すと\(\frac{３}{５}\)＞\(\frac{３}{７}\)になるね。

「分数の大きさ」のまとめ

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。