「交かんのきまり・結合のきまり・分配のきまり」わかりやすく解説

小学校４年生の算数で学習する「計算のきまり」のうち、「交かんのきまり（交換法則）」「結合のきまり（結合法則）」「分配のきまり（分配法則）」についてわかりやすく解説するよ。

どうしてそのきまりが成り立つのか、どう便利なのかをくわしく紹介していくよ。

「交かんのきまり・結合のきまり・分配のきまり」わかりやすく解説のPDF（13枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

交かんのきまり（交換法則）

「交かんのきまり」っていうのは、つまり「数字のじゅんばんを交かんしてもいいよー」ということ。

交かんのきまり

〇＋△＝△＋〇　←たす順番を交かんしても答えは同じ
（例）５＋６＝６＋５
〇×△＝△×〇　←かける順番を交かんしても答えは同じ
（例）５×６＝６×５

それぞれ、式の中の２つの数字の位置を交かんしているけれど、答えは変わらないよね。

でも、どうしてわざわざ位置を交かんしたりする必要があるの？と思うよね。

数字の位置を交かんすると、計算がラクになることがあるんだ。

たとえば、交かんのきまりを使って
「２５×７×４」の計算をしてみよう。

たろう

２５×７の計算ってめんどうくさいなー。

「２５×７」を計算するには、筆算しないとむずかしかったりするよね。
さらに、２５×７をしたあとに、さらにまた４をかけるのに筆算が必要だね。
ちょっと大変だよね。

そこで、さっきしょうかいした
「〇×△＝△×〇　←かける順番を交かんしても答えは同じ」を使おう。

　２５×７×４　←７と４の位置を交かんするよ
＝２５×４×７　←２５×４＝１００になることは覚えておくと便利
＝１００×７
＝７００

交かんのきまりを使うと、２５×７をしなくても、かんたんに答えを求めることができたね。
今回登場した、「２５×４＝１００」は、便利なのでぜひ覚えておこう。

「交かんのきまり」で気をつけることは次の２つだよ。

「交かんのきまり」で気をつけること

交かんのきまりはたし算とかけ算で使える
交かんのきまりはひき算とわり算では使えない
「５－２」と「２－５」では、答えがちがってしまうね。
「６÷２」と「２÷６」も、答えがちがってしまうね。

交かんのきまりは、たし算とかけ算でしか使えないので、注意しようね。

結合のきまり（結合法則）

結合のきまり（結合法則ほうそく）っていうのは、たし算だけでできた式と、かけ算だけでできた式では、どこに（　）をつけても、答えは同じになるという計算のきまりだよ。

結合のきまり（結合法則）

〇＋△＋▢＝（〇＋△）＋▢＝〇＋（△＋▢）
（例）４＋２＋３＝（４＋２）＋３＝４＋（２＋３）
〇×△×▢＝（〇×△）×▢＝〇×（△×▢）
（例）４×２×３＝（４×２）×３＝４×（２×３）

先に〇と△を計算しようが、
先に△と▢を計算しようが答えは変らないってことだよ。

「結合（けつごう）」とは、くっついて１つになることだよ。
計算の式のなかで（　）をつけると、その（　）の中の計算を先にするんだったよね。
つまり、２つの数字を先に１つにまとめてしまうイメージかな。

これも、どうして式の中で２つの数字を先にまとめる必要があるの？と思うよね。

やっぱり、先にまとめることで、計算がラクになるからだよ。

たとえば、結合のきまりを使って
「５４＋７３＋２７」の計算をしてみよう。

前から順番に計算するとしたら、５４＋７３の計算は大変だよね。

さっきしょうかいした
「〇＋△＋▢＝（〇＋△）＋▢＝〇＋（△＋▢）」のきまりを使おう。

　５４＋７３＋２７　　←「７３＋２７」にかっこ（　）をつける
＝５４＋（７３＋２７）←７３＋２７＝１００になる
＝５４＋１００
＝１５４

７３＋２７＝１００になることに気づければすぐに計算できるよね。

「１３×２５×４」の計算をしてみよう。

前から順番に計算するとしたら、１３×２５の計算は大変だよね。

さっきしょうかいした
「〇×△×▢＝（〇×△）×▢＝〇×（△×▢）」を使おう。

　１３×２５×４　　←「２５×４」にかっこ（　）をつける
＝１３×（２５×４）←２５×４＝１００になる
＝１３×１００
＝１３００

２５×４＝１００になることに気づければすぐに計算できるよね。

「１２×１２５×８」の計算をしてみよう。

前から順番に計算するとしたら、１２×１２５の計算は大変だよね。

さっきしょうかいした
「〇×△×▢＝（〇×△）×▢＝〇×（△×▢）」を使おう。

　１２×１２５×８　　←「１２５×８」にかっこ（　）をつける
＝１２×（１２５×８）

１２５×８＝１０００になることを覚えておくと便利だよ。

＝１２×１０００
＝１２０００

１２５×８＝１０００になることに気づければすぐに計算できるよね。

「結合のきまり」も、つかえる式とそうでない式があるので注意が必要だよ。

気をつけること

結合のきまりはたし算のみの式とかけ算のみの式で使える
結合のきまりはひき算やわり算がある式では使えない

たろう

結合のきまりはひき算やわり算がある式では使えないってどういうこと？

結合のきまりはひき算がある式では使えない

たとえば、９－５＋３を前からじゅんばんに計算すると
　９－５＋３
＝４＋３
＝７

同じ問題を
かっこをつけて、「５＋３」を先に計算してみよう。
　９－５＋３
＝９－（５＋３）
＝９－８
＝１

答えがさっきとちがっているよね。
つまり、ひき算がある式では結合のきまりは使えないということなんだ。

結合のきまりはわり算がある式では使えない

同じように１２÷３×２を考えてみよう。
　１２÷３×２
＝４×２
＝８

同じ問題を
かっこをつけて、「３×２」を先に計算してみよう。
　１２÷３×２
＝１２÷（３×２）
＝１２÷６
＝２

答えがさっきとちがっているよね。
つまり、わり算がある式でも結合のきまりは使えないということなんだ。

分配のきまり（分配法則）

「分配ぶんぱいのきまり」は、「分配」という漢字の意味を考えるとわかるとおり、数字を「分わ」けて「配くば」ることだよ。

分配のきまりのイメージは
▢を分けて配っている感じ

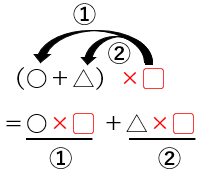
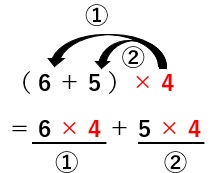
▢を順番にかっこの中の数字にかけていくよ。
まず〇と▢をかけて（➀）、次に△と▢をかける（➁）。

下のように
かっこ（　）の中が「＋」じゃなくて「−」になっているバージョンもあるよ。

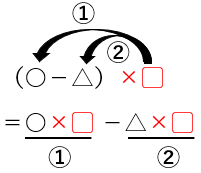
分配のきまりについてまとめると次の通りだよ。

分配のきまり

（〇＋△）×▢＝〇×▢＋△×▢
　（例）（３＋２）×４＝３×４＋２×４
（〇－△）×▢＝〇×▢－△×▢
　（例）（３－２）×４＝３×４－２×４

「分配のきまり」も、やっぱり計算をラクにするためにつかうことができるよ。

「（１００＋２）×２５」を計算してみよう。

たろう

かっこ（　）の中から計算すると、１０２×２５になって計算が大変そう・・。

さっきしょうかいした「分配のきまり」
「（〇＋△）×▢＝〇×▢＋△×▢」を使おう。

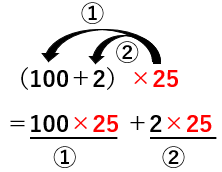
①１００×２５＝２５００
②２×２５＝５０
とかんたんに計算できるね。

だから答えは次のようになるよ。

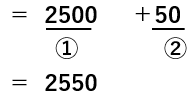
分配のきまりが成り立つ理由

算数の公式やきまりなどは、「どうしてそれが成り立つのか？」をわかっているかどうかで、応用問題でも解くことができる「算数力」がアップするよ。

少しむずかしいかもしれないけど、なぜ分配のきまりが成り立つのかを考えてみよう。

下の図のように〇が並んでいるとするよ。
〇の数は全部で何個かな？

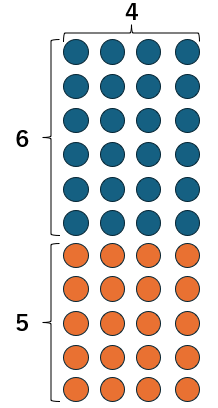
そう。４４個だね。
では、どうやって求めるかな？

求め方①

大きな長方形として考えて求めてみるよ。

たてが６＋５＝１１こ、横が４こだから、１１×４＝４４こ

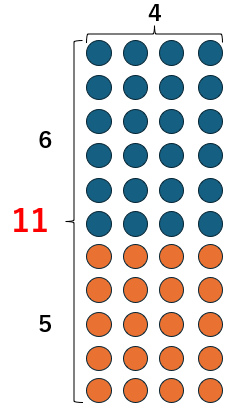
１つの式にすると
（６＋５）×４
になるね。

求め方②

青い〇とオレンジの〇でできている、２つの長方形が合わさった形として考えてみるよ。

青い〇の長方形は、たてが６こ、横が４こだから、６×４＝２４こ
オレンジの〇の長方形は、たてが５こ、横が４こだから、５×４＝２０こ

２つの長方形を合わせて２４＋２０＝４４こだね。

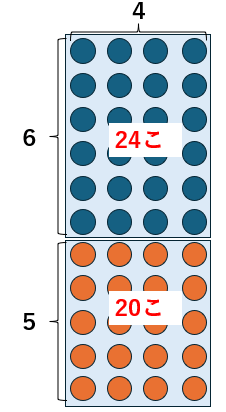
１つの式にすると、
６×４＋５×４
になるね。

分配のきまりが成り立つ理由

〇の数の求め方を式で表すと、「（６＋５）×４」と「６×４＋５×４」の２通りの式があったよね。

どちらも答えは「４４こ」になるから、２つの式は等しいということだよね。
つまり、
（６＋５）×４＝６×４＋５×４
だといえるね。

まさに「分配のきまり」で説明したとおりだよね。

計算のきまり「交かんのきまり・結合のきまり・分配のきまり」のまとめ