２桁で割る割り算の筆算のやり方をわかりやすく解説（練習問題）
小学校４年生で学習する「わり算の筆算」について、「わる数」が２けたの場合の「２桁で割る割り算の筆算」のやり方をわかりやすく解説するよ。
商の見当をつけるコツやポイントも紹介しているよ。
目次
今までは、「８４÷２」「８５２÷４」のような
１けたの数でわる「わり算」の筆算を勉強してきたね。
今回は「４８÷２３」や「１５３÷２４」のような２けたの数でわる「わり算」の筆算をやっていこう。
ただ、今までのわり算をわかっていればできるから安心してね。
もし、今までのわり算がわかっていなかったら見直しておこう。
２けた÷２けたの筆算
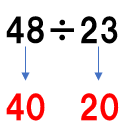
４８÷２３を筆算を使って計算しなさい。
まず、わり算の筆算は次のように書いたよね。
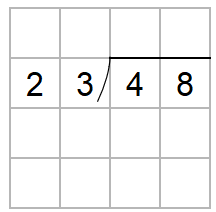
家の屋根みたいな記号を使って、
わられる数が家の中で、わる数が外に出るんだったよね。
さっそく筆算をしていこう。
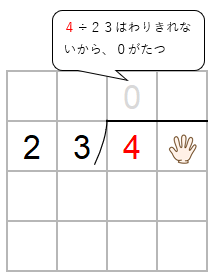
４８って、十の位と一の位があるんだけれど、筆算をするときには、十の位と一の位、順番に計算をするんだ。
まずは、十の位だけをわり算するよ。
なので、一の位は「ちょっとまっていてね」と、手でかくしてしまおう。
一の位をかくすと、４÷２３になるね。
ただ、わりきれないから、商に「０」をたてよう。
ここで「かくしていた一の位」の出番だよ。
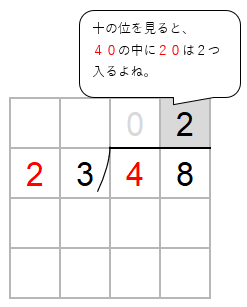
４８の中に２３がいくつ入るか考えよう。
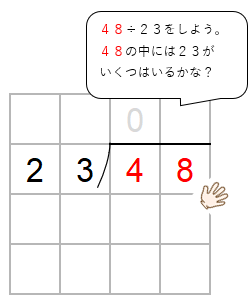
コツは、十の位の数に注目して、かりの商をたてること。
４８→４０
２３→２０として考えると、４０の中に２０は２つ入るよね。
だから、とりあえず商として「２」をたてておこう。
かりの商の見つけ方（商の見当をつける コツ）
- わられる数、わる数を、何十の数と見て、商を見つける
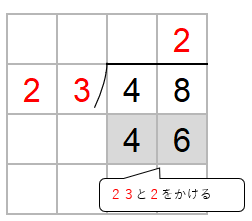
次に、わる数２３と一の位の上にたてた２をかけた数を４８の下に書くよ。
４８から４６をひくよ。
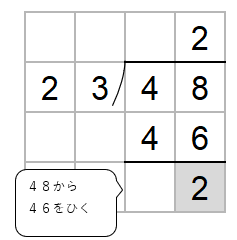
ここでチェックすることがあったね。
ひき算した数がわる数２３より小さいかをかくにんしよう。
２は２３より小さいからOKだね。
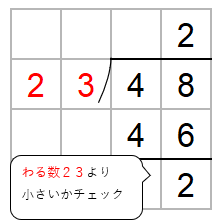
ということは、かりの商「２」は正しいことがわかるよ。
答えは「４８÷２３＝２あまり２」と求めることができたね。
かりの商がちがっていた場合
かりの商がちがっていたら、「筆算の計算がどうなるのか」や「どうしたらいいのか」をしょうかいするね。
かりの商を小さくする場合
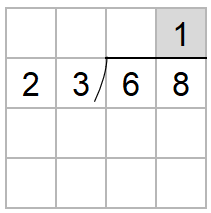
６８÷２３で一の位の上にたつ商を考えよう。
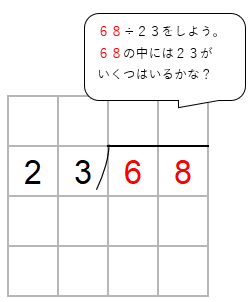
コツは、十の位の数に注目して、かりの商をたてることだったね。
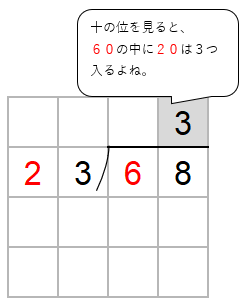
６８→６０
２３→２０として考えると、６０の中に２０は３つ入るよね。
だから、とりあえず、商として「３」をたてておこう。
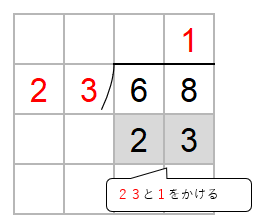
次に、わる数２３と一の位の上にたてた３をかけた数を６８の下に書くよ。
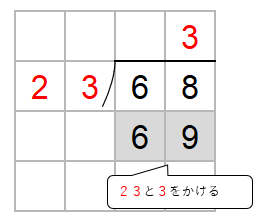
６８から６９をひきたいんだけど、ひくことができないよね。
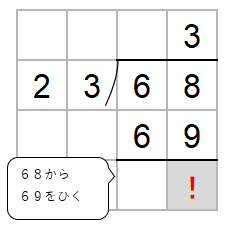
かりの商「３」がちがうんだ。
だから、かりの商「３」を１つ小さくしてみよう。
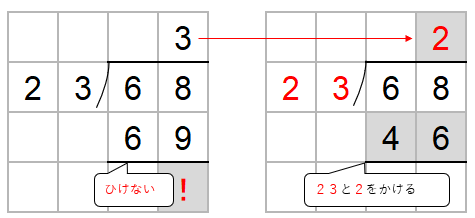
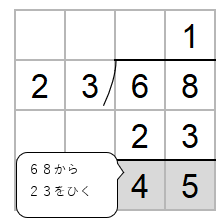
あとは、今まで同じように筆算をしていけばいいね。
６８から４６をひくよ。
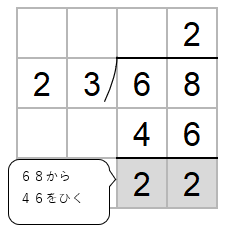
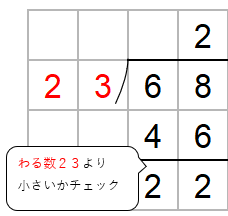
ここでチェックすることがあったね。
ひき算した数がわる数２３より小さいかをかくにんしよう。
２２は２３より小さいからOKだね。
くまごろうかりの商がちがっていると、ひき算ができなくなるんだ。
そういうときは、かりの商を１つ小さくするといいよ。
かりの商を大きくする場合
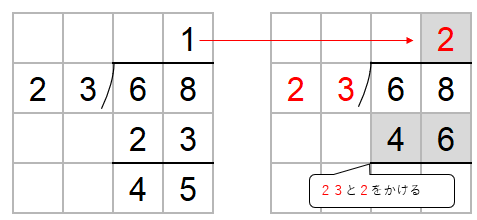
６８÷２３で一の位の上に「１」をたてたとしよう。
次に、わる数２３と一の位の上にたてた１をかけた数を６８の下に書くよ。
６８から２３をひこう。
ここでチェックすることがあったね。
ひき算した数がわる数２３より小さいかをかくにんしよう。
ひき算した数は４５だから、わる数より小さくないよね。
ということは、かりの商「１」がまちがっていることになるんだ。
だから、かりの商「１」を１つ大きくしてみよう。
くまごろうかりの商がちがっていると、ひき算したあとの数が「わる数」より大きくなるんだ。
そういうときは、かりの商を１つ大きくするといいよ。
３けた÷２けたの筆算
１５３÷２４を筆算を使って計算しなさい。
わり算の筆算は次のように書いたよね。
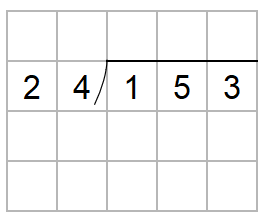
１５３って、百の位と十の位と一の位があるんだけれど、筆算をするときには、百の位と十の位と一の位、順番に計算をするんだ。
まずは、百の位だけをわり算するよ。
なので、十の位と一の位は「ちょっとまっていてね」と、手でかくしてしまおう。
十の位と一の位をかくすと、１÷２４になるね。
ただ、わりきれないから、商に「０」をたてよう。
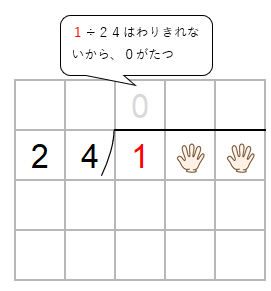
ここで「かくしていた十の位」の出番だよ。
１５の中に２４がいくつ入るか考えよう。
ただ、わりきれないから、商に「０」をたてよう。
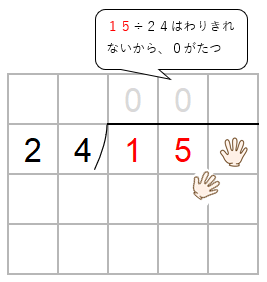
最後に「かくしていた一の位」の出番だよ。
１５３の中に２４がいくつ入るか考えよう。
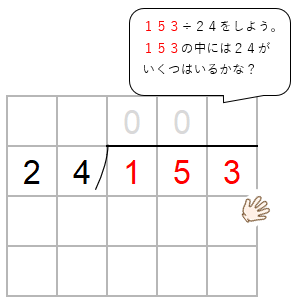
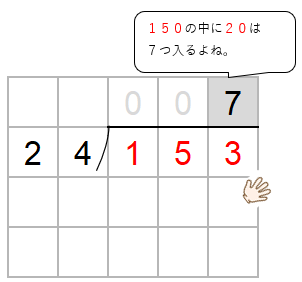
コツは、十の位の数に注目して、かりの商をたてること。
１５３→１５０
２４→２０として考えると、１５０の中に２０は７つ入るよね。
だから、とりあえず商として「７」をたてておこう。
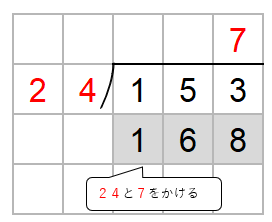
次に、わる数２４と一の位の上にたてた７をかけた数を１５３の下に書くよ。
１５３から１６８をひきたいんだけど、ひくことができないよね。
ということはかりの商「７」がちがうんだ。
だから、かりの商「７」を１つ小さくしてみよう。
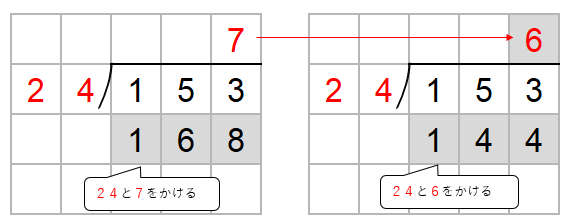
あとは、今まで同じように筆算をしていけばいいね。
１５３から１４４をひくよ。
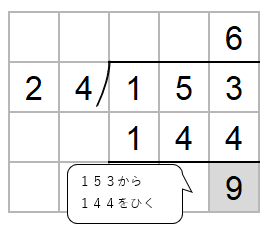
ここでチェックすることがあったね。
ひき算した数がわる数２４より小さいかをかくにんしよう。
９は２４より小さいからOKだね。
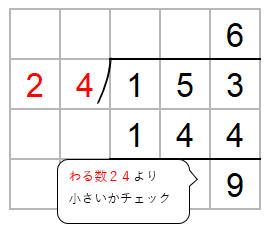
答えは「１５３÷２４＝６あまり９」と求めることができたね。
７１３÷４１を筆算を使って計算しなさい。
わり算の筆算は次のように書いたよね。
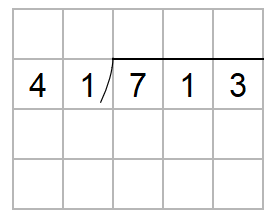
７１３って、百の位と十の位と一の位があるんだけれど、筆算をするときには、百の位と十の位と一の位、順番に計算をするんだ。
まずは、百の位だけをわり算するよ。
なので、十の位と一の位は「ちょっとまっていてね」と、手でかくしてしまおう。
十の位と一の位をかくすと、７÷４１になるね。
ただ、わりきれないから、商に「０」をたてよう。
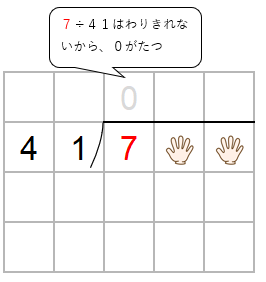
ここで「かくしていた十の位」の出番だよ。
７１の中に４１は１つ入るよね。
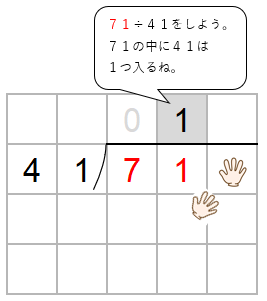
わる数４１と一の位の上にたてた１をかけた数を７１の下に書くよ。
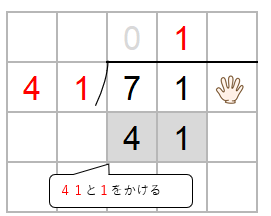
７１から４１をひこう。
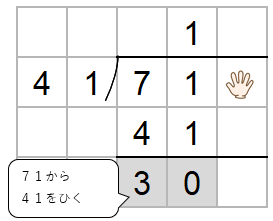
ひき算した数がわる数４１より小さいかをかくにんしよう。
３０は４１より小さいからOKだね。
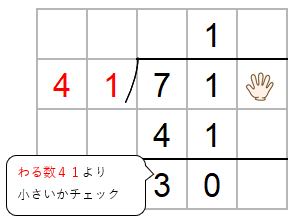
最後に「かくしていた一の位」の出番だよ。
一の位の「３」を下におろそう。
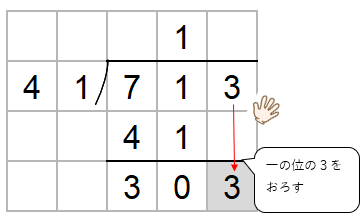
３０３の中に４１はいくつ入るかを考えよう。
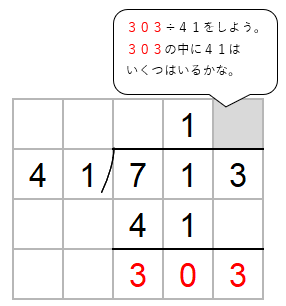
コツは、十の位の数に注目して、かりの商をたてること。
３０３→３００
４１→４０として考えると、３０３の中に４０は７つ入るよね。
だから、とりあえず、商として「７」をたてておこう。
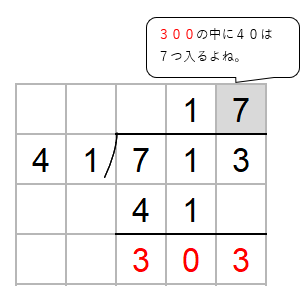
次に、わる数４１と一の位の上にたてた７をかけた数を３０３の下に書いてひき算するよ。
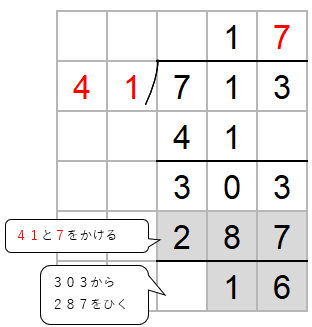
ここでチェックすることがあったね。
ひき算した数がわる数４１より小さいかをかくにんしよう。
１６は４１より小さいからOKだね。
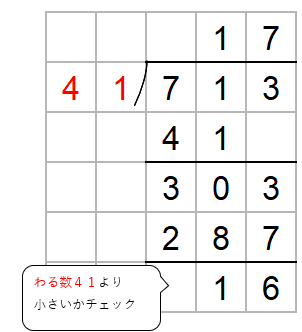
答えは「７１３÷４１＝１７あまり１６」と求めることができたね。
２けたでわる筆算の練習問題
８４÷２０を筆算を使って計算しなさい。
わり算の筆算は次のように書いたよね。
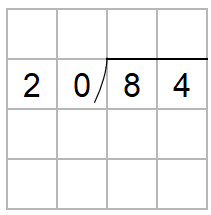
８４って、十の位と一の位があるんだけれど、筆算をするときには、
十の位と一の位、順番に計算をするんだったよね。
まずは、十の位だけをわり算するよ。
なので、一の位は「ちょっとまっていてね」と、手でかくしてしまおう。
一の位をかくすと、８÷２０になるね。
ただ、わりきれないだから、商に「０」をたてよう。
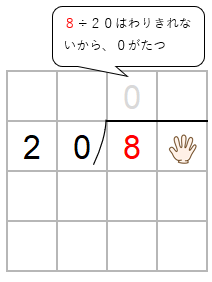
ここで「かくしていた一の位」の出番だよ。
８４の中に２０がいくつ入るか考えよう。
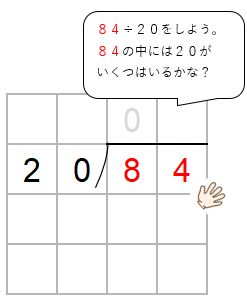
コツは、十の位の数に注目して、かりの商をたてること。
８４→８０
として考えると、８０の中に２０は４つ入るよね。
だから、とりあえず、商として「４」をたてておこう。
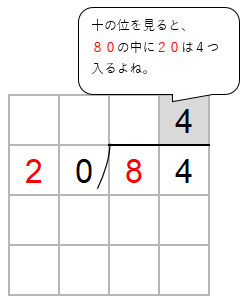
次に、わる数２０と一の位の上にたてた４をかけた数を８４の下に書くよ。
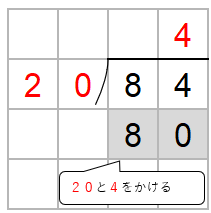
８４から８０をひくよ。
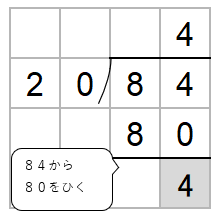
ここでチェックすることがあったね。
ひき算した数がわる数２０より小さいかをかくにんしよう。
４は２０より小さいからOKだね。
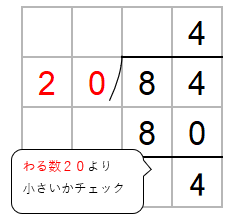
ということは、かりの商「４」は正しいことがわかるよ。
「８４÷２０＝４あまり４」と求めることができたね。
６０÷１９を筆算を使って計算しなさい。
わり算の筆算は次のように書いたよね。
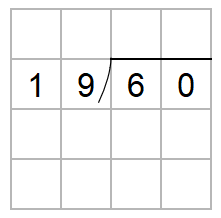
６０って、十の位と一の位があるんだけれど、筆算をするときには、
十の位と一の位、順番に計算をするんだったよね。
まずは、十の位だけをわり算するよ。
なので、一の位は「ちょっとまっていてね」と、手でかくしてしまおう。
一の位をかくすと、６÷１９になるね。
ただ、わりきれないよね。だから、商に「０」をたてよう。
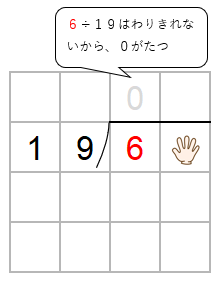
ここで「かくしていた一の位」の出番だよ。
６０の中に１９がいくつ入るか考えよう。
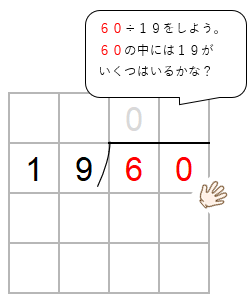
コツは、十の位の数に注目して、かりの商をたてること。
１９→１０
として考えると、６０の中に１０は６つ入るよね。
だから、とりあえず、商として「６」をたてておこう。
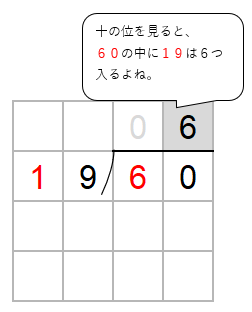
次に、わる数１９と一の位の上にたてた６をかけた数を６０の下に書くよ。
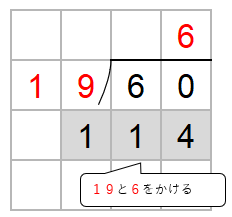
どう考えても６０から１１４はひくことができないから、かりの商「６」を１つ小さくしよう。
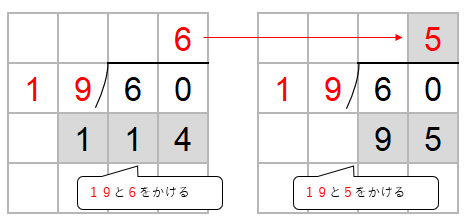
６０から９５はひくことができないから、かりの商「５」を１つ小さくしよう。
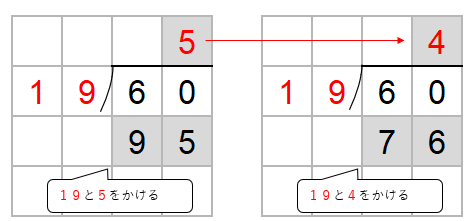
６０から７６はひくことができないから、かりの商「４」を１つ小さくしよう。
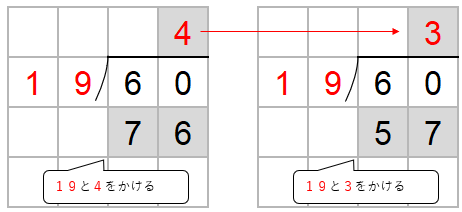
６０から５７をひくことはできるから、商は「３」になることがわかったね。
あとは今まで同じように６０から５７をひこう。
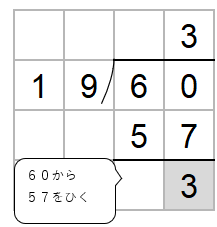
ここでチェックすることがあったね。
ひき算した数がわる数１９より小さいかをかくにんしよう。
３は１９より小さいからOKだね。
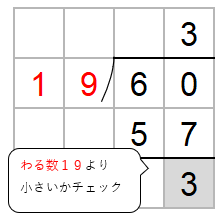
「６０÷１９＝３あまり３」と求めることができたね。
６８４÷２１を筆算を使って計算しなさい。
わり算の筆算は次のように書いたよね。
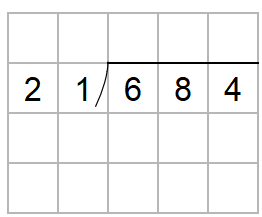
６８４って、百の位と十の位と一の位があるんだけれど
筆算をするときには、百の位と十の位と一の位、順番に計算をするんだ。
まずは、百の位だけをわり算するよ。
なので、十の位と一の位は「ちょっとまっていてね」と、手でかくしてしまおう。
十の位と一の位をかくすと、６÷２１になるね。
ただ、わりきれないから、商に「０」をたてよう。
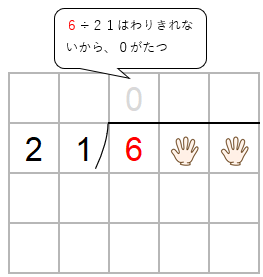
ここで「かくしていた十の位」の出番だよ。
６８の中に２１は３つ入るよね。
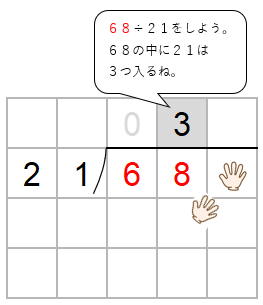
わる数２１と一の位の上にたてた３をかけた数を６８の下に書くよ。
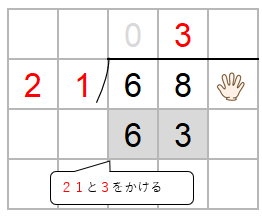
６８から６３をひこう。
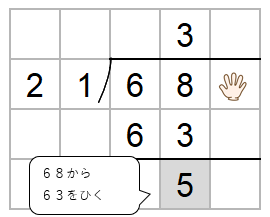
ひき算した数がわる数２１より小さいかをかくにんしよう。
５は２１より小さいからOKだね。
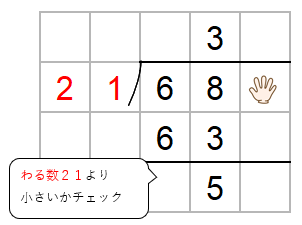
最後に「かくしていた一の位」の出番だよ。
一の位の「４」を下におろそう。
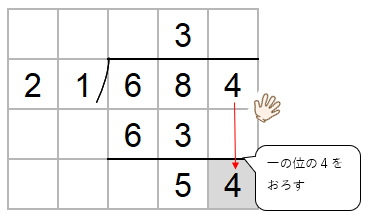
５４の中に２１はいくつ入るかを考えよう。
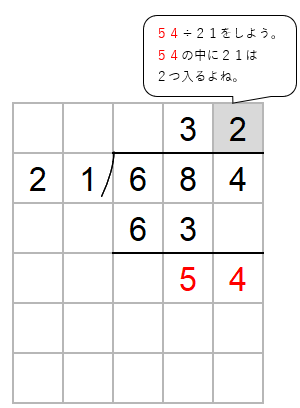
次に、わる数２１と一の位の上にたてた２をかけた数を５４の下に書いてひき算するよ。
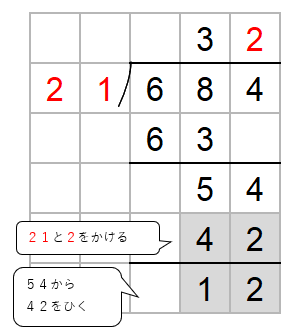
ここでチェックすることがあったね。
ひき算した数がわる数２１より小さいかをかくにんしよう。
１２は２１より小さいからOKだね。
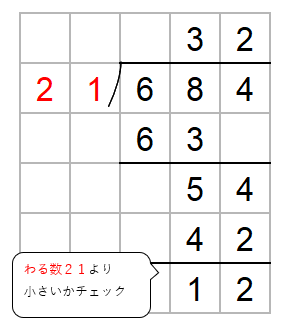
答えは「６８４÷２１＝３２あまり１２」と求めることができたね。
「わり算の筆算のやり方（２けたでわる筆算）」まとめ
「わり算の筆算のやり方（２けたでわる筆算）」まとめ
- わられる数、わる数を、何十の数と見て、かりの商を見つける。
- かりの商がちがっていると、ひき算ができなくなる。
そういうときは、かりの商を１つ小さくする。 - かりの商がちがっていると、ひき算したあとの数が「わる数」より大きくなる。
そういうときは、かりの商を１つ大きくする。
運営者情報
ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。
