「かけ算のきまり」かけ算のきまりを使ってくふうして計算する方法

小学校３年生の算数で学習する「かけ算のきまり」について、かけ算にはどんなきまりがあるのか、かけ算のきまりを使って、くふうして計算する方法をわかりやすく解説するよ。

かける数が１ふえたり、１へると答えはどうなるのか、かける数とかけられる数を入れかえたり、分けたりするばあいはどうなるのか、１０より大きい数のかけ算をくふうして計算する方法をくわしく紹介するよ。

「かけ算のきまり」の問題に挑戦できる自動採点機能付きのドリルもあるよ！

ゆみねこドリル「かけ算のきまり」のドリルページへ

「かけ算のきまり」かけ算のきまりを使ってくふうして計算する方法のPDF（15枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

「かけ算のきまり」とは
「かける数が１ふえる・かける数が１へる」きまり
「かける数とかけられる数を入れかえる」きまり
「かけられる数・かける数を分ける」きまり
１０より大きい数のかけ算をくふうして計算しよう
まとめ

「かけ算のきまり」とは

２年生で勉強した「かけ算（九九）」は、１から９までの数を、それぞれかけるといくつになるのか？ということだったね。

３年生では、「かけ算には、どういうきまり（ルール）があるのか？」を勉強するよ。

ルールといってもかんたん。
「かける数が１ふえたり、へったりすると、答えってどうなるの？」とか、「かける数とかけられる数を、ひっくり返したらどうなるのか？」とか、
「かける数を２つにわけたら、答えはどうなるのか？」ということを勉強するんだよ。

たろう

どうしてそんなルールを勉強するの？

くまごろう

かけ算のルールを知っていると、ちょっとむずかしいかけ算でも、くふうしてカンタンに計算することができたりするんだ。

では、さっそくどんなルールがあるのか、ひとつずつ見てみよう。

「かける数が１ふえる」・「かける数が１へる」ときのきまり

みんなは２年生の時に、九九をがんばっておぼえたよね。
もし、「７×１＝７」「７×２＝１４」「７×３＝２１」「７×４＝・・・あれ・・・なんだっけ？」となったらどうしたらいいかな？

こんなときに、「かける数が１ふえると、答えはどうなるか」のルールを知っていると、すぐにわかるんだ。

「７×１＝７」「７×２＝１４」「７×３＝２１」「７×４＝？」を、表にまとめてみるよ。

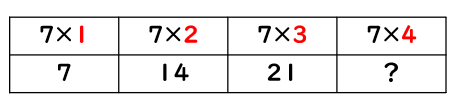
表を見ると、「７×１」「７×２」「７×３」というように、「かける数が１ふえる」と、答えは「７→１４→２１」というように、「７ずつ大きくなっているのがわかるかな？」

この「７」って、「かけられる数」だよね。
ということは、「かける数が１ふえると、答えはかけられる数（７）だけ大きくなっている」ということがわかるね。

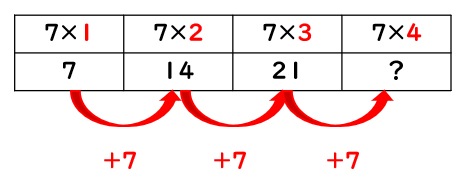
ということは、「７×４」はどうなるだろう。
九九をわすれてしまっていても、「７×３」より「７」ふえることがわかっていれば、「７×３」の答えの「２１」に「７」をたしてあげて、もとめることができるね。

２１＋７＝２８なので、「７×４＝２８」とわかるね。

たろう

ほんとうだ。かけ算のルールを知っていればあんしんだね。

「かける数が１ふえる」と、答えはかけられる数だけ大きくなることがわかったけれど、はんたいに、「かける数が１へる」とどうなるんだろう？

もういちど表を見てみよう。

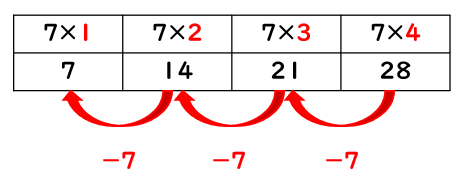
かける数が１へると、答えはかけられる数「７」だけ小さくなるともいえるよね。

「かける数が１ふえる」・「かける数が１へる」のきまりをまとめるよ。

「かける数が１ふえる」・「かける数が１へる」ときのきまり

かける数が１ふえると、答えはかけられる数だけ大きくなる。

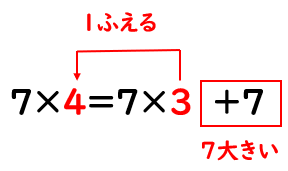
かける数が１へると、答えはかけられる数だけ小さくなる。

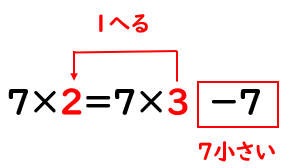
「かける数が１ふえる」・「かける数が１へる」きまりを図でかくにんしよう

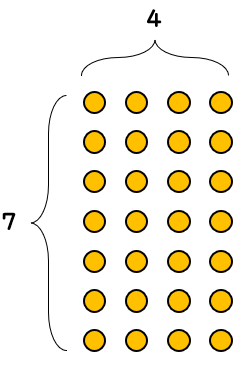
「７×４」は、次のように図で表すことができるよね。

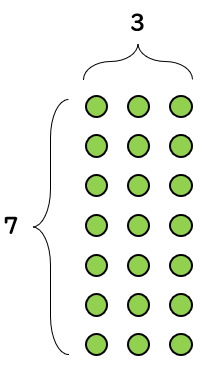
おなじように図で表すと、「７×３」は次のようになるよね。

「７×４」と「７×３」の図をくらべると、「７×４」の方が、かけられる数の「７」の分だけ大きくなっていることがわかるかな。

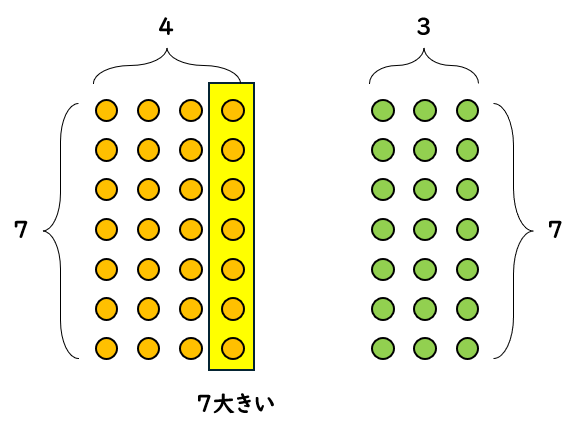
「かける数が１ふえると、答えはかけられる数（７）だけ大きくなる」ということが、図でもせつ明できたね。

「かける数が１ふえる」・「かける数が１へる」きまりを式で表そう

これまで、「かける数が１ふえると、答えはかけられる数だけ大きくなる」ことと、「かける数が１へると、答えはかけられる数だけ小さくなる」ということをことばや図でかくにんしてきたね。

でも、ことばや図だと、せつ明するのがたいへんだよね。
そこで、「式で表す」とどうなるか、かんがえてみよう。

「７×４」は、「７×３」よりも「７大きい」んだよね。
これを式で表すと、
７×４＝７×３＋７
となるよ。

「７×４」は（＝）「７×３」より７大きい（＋７）だね。

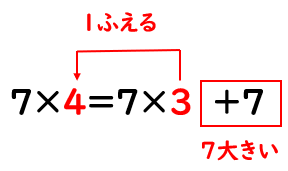
この式は、問題のときによく出てくるかたちなんだ。
さっそく、問題をときながら　かくにんしてみよう。

「かける数が１ふえる」・「かける数が１へる」きまりの練習問題

▢にあてはまる数はいくつでしょう。

７×４＝７×３＋▢

かけられる数が３から４と１ふえると、
かけられる数「７」だけ大きくなるから、
▢に入る数は７だよ。

▢にあてはまる数はいくつでしょう。

６×２＝６×３－▢

かけられる数が３から２と１へると、
かけられる数「６」だけ小さくなるから、
▢に入る数は６だよ。

▢にあてはまる数はいくつでしょう。

６×８－６＝６×▢

６×８より６小さいってことは、図で考えると次のようなイメージだね。

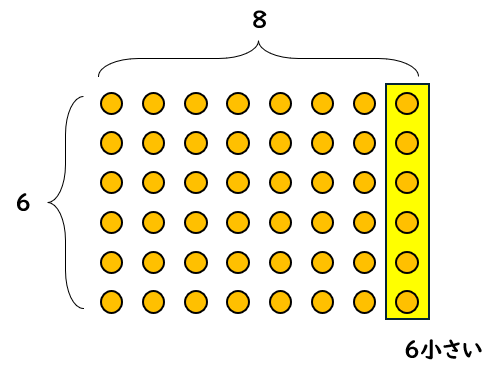
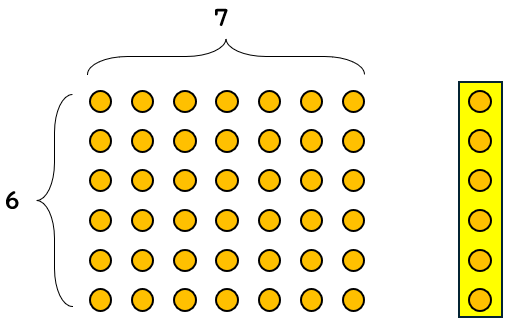
だから、「６×８－６＝６×▢」の▢に入る数は「７」とわかるよ。

「かける数と、かけられる数を入れかえる」ときのきまり

こんどは、「かける数」と「かけられる数」を入れかえると、答えはどうなるのか　たしかめてみよう。

４×７＝２８だよね。
では、「かける数」の「７」と、「かけられる数」の「４」を入れかえてみるよ。
答えは、７×４＝２８になるよね。

もうひとつたしかめてみよう。
８×２＝１６だよね。
８と２をいれかえてみると、２×８＝１６になるね。

たろう

「かける数とかけられる数」を入れかえても、答えは変わらないんだね！

そう、「かけられる数とかける数」には次のきまりがあるんだ。

「かけられる数とかける数を入れかえる」ときのきまり

かけられる数とかける数を入れかえて計算しても、答えは同じに
なる。

「かけられる数とかける数を入れかえる」きまりを図でかくにんしよう

「５×７」を表す図で考えてみよう。

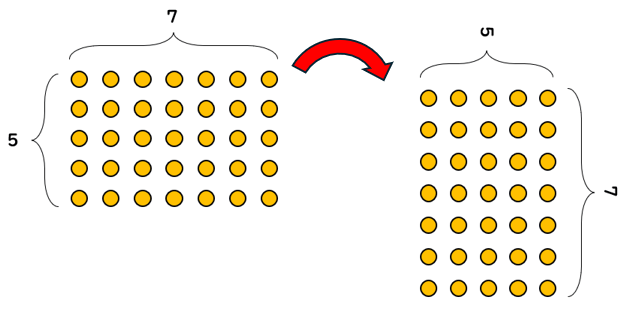
「５×７」の図を直角に回してみると、たてが７、よこが５になって、
「７×５」を表す図と同じになるよね。

だから、かけられる数とかける数を入れかえて計算しても、答えは同じになると言えるんだね。

「かけられる数とかける数を入れかえる」きまりの練習問題

▢にあてはまる数はいくつでしょう。

７×４＝▢×７

２つの式が、「＝」でむすばれているね。
ということは、２つの式の答えは同じになるということ。

２つの式の答えが同じということは、「かけられる数」と「かける数」が入れかわっているだけ、ということがわかるね。

かけられる数「７」とかける数「４」を入れかえているので、▢には４が入るよ。

「かけられる数・かける数を分ける」きまり

〇×▢みたいなかけ算があったとき、かける数〇を２つにわけたり、かけられる数▢を２つに分けると、答えはどうなるかな？

じゅん番にかくにんしてみよう。

かけられる数を分ける

①９×７＝６３
かけられる数「９」を「５」と「４」にわけて、「５」と「４」の２つにそれぞれ「７」をかけてみよう。

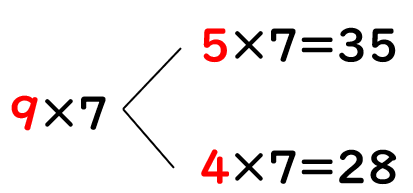
あわせると「３５＋２８＝６３」になるよね。
９×７と同じ答えになったね。

②８×６＝４８
かけられる数「８」を「１」と「７」にわけて、「１」と「７」の２つにそれぞれ「６」をかけてみよう。

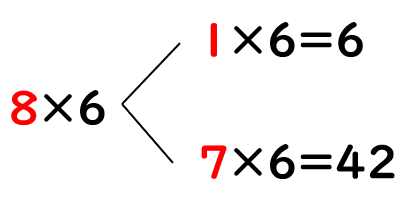
あわせると「６＋４２＝４８」になるよね。
８×６と同じ答えになったね。

つまり次のきまりがわかるんだ。

「かけられる数を分ける」きまり

かけ算では、かけられる数を分けて計算しても、答えは同じになる。

かける数を分ける

こんどは「かける数」を分けてみるよ。

①７×５＝３５
かける数「５」を「２」と「３」にわけて、「７」に、「２」と「３」の２つの数をかけてみよう。

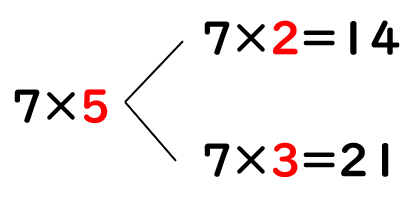
あわせると「１４＋２１＝３５」になるよね。
７×５と同じ答えになったね。

②９×９＝８１
かける数「９」を「２」と「７」にわけて、「９」に、「２」と「７」の２つの数をかけてみよう。

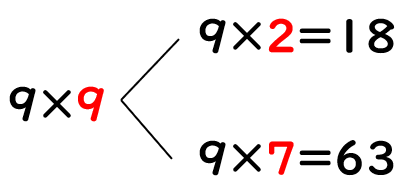
あわせると「１８＋６３＝８１」になるよね。
９×９と同じ答えだね。

このことから次のきまりがわかるよ。

「かける数を分ける」きまり

かけ算では、かける数を分けて計算しても、答えは同じになる。

「かけられる数・かける数を分ける」きまりを図でかくにんしよう

「５×７」の、かけられる数「５」を分けたばあいを、図で考えてみよう。

たとえば、かけられる数「５」を「３」と「２」に分けたとするよ。
図で表すと、こんなイメージになるね。

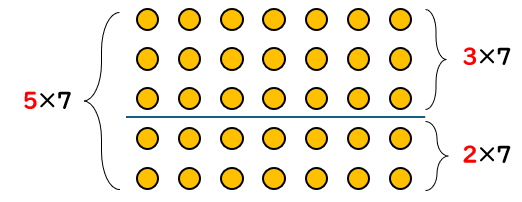
図を見ると、「５×７」を表す図と、「３×７」と「２×７」をあわせた図は、同じことがわかるね。

「かけられる数・かける数を分ける」きまりの練習問題

▢にあてはまる数はいくつでしょう。

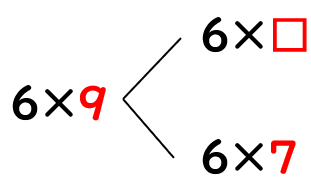
かける数「９」を分けていることがわかるね。
かた方が「７」だから、「９－７＝２」だから、▢には「２」が入るよ。

「１０より大きい数のかけ算」をくふうして計算しよう

みんなが２年生で勉強した九九は、１から９までの数のかけ算だったよね。
だから、１０より大きい数のかけ算はできないよね。

かけ算のきまりを知っていると、計算のくふうができるんだったよね。
「かけられる数・かける数を分ける」きまりを使うと、１０より大きい数のかけ算ができるようになるんだ。

たとえば「１３×６」の計算をやってみよう。

かけられる数の「１３」を２つの数に分けて考えるよ。
たとえば、「８」と「５」にわけると次のようになるね。

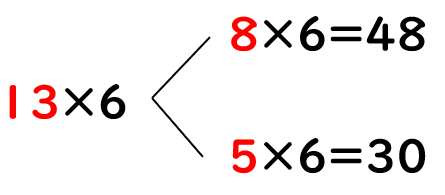
あわせると「４８＋３０＝７８」になるよね。
かけ算では、かけられる数を分けて計算しても答えは同じになるのだから、
「１３×６」も答えは「７８」になると　もとめることができたね。

同じように、８×１８を計算してみよう。
かける数の「１８」を「９」と「９」にわけると次のようになるよ。

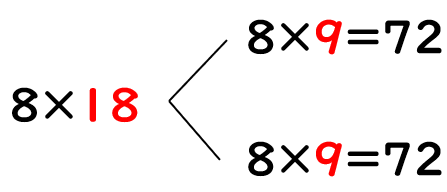
あわせると「７２＋７２＝１４４」になるよね。
「８×１８」は答えが「１４４」になると　もとめることができたね。

「１０より大きい数」のかけ算のポイントは次の通りだよ。

「１０より大きい数」のかけ算のポイント

「１３×６」や「８×１８」のような「１０より大きい数」のかけ算も、かけられる数・かけられる数を分ければ、１から９の九九のかけ算を使ってもとめることができる。