「0や1のわり算」0を割るとどうなるのか?をわかりやすく解説
小学校3年生の算数で学習する「0や1のわり算」について、0をわるとどうなるのか、1でわるとどうなるのかをわかりやすく かいせつするよ。
0でわることができないりゆう についても、くわしくしょうかいしているよ。
0を割るとどうなるのか?「0のわり算」
今まで、「12÷4」「8÷2」「6÷3」のようなわり算をやってきたよね。
今回は「0をわるとどうなるのか?」や、「1でわるとどうなるのか?」を考える、「0や1のわり算」について勉強していくよ。
まず、0のわり算について勉強していこう。
次の数のあめを、4人で同じ数ずつ分けます。1人分は何こになるかをそれぞれ考えてみましょう。
8このあめを4人で分ける
8このあめを4人で分けると、1人分は
8÷4=2こになるね。
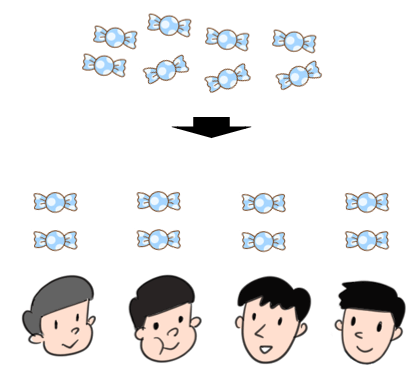
4このあめを4人で分ける
4このあめを4人で分けると、1人分は
4÷4=1こになるね。
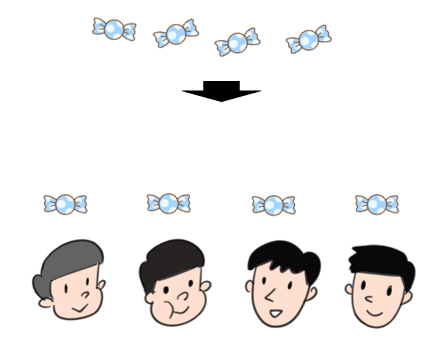
0このあめを4人で分ける
いよいよ、「0をわる」ばあいだね。
「0このあめ」ということは、「あめがない」ということだね。
「あめがない」のだから、何人で分けたとしても、「1人分は0こ」だよね。

式で表すと、
0÷4=0となるよ。
この計算が、0をわる「0のわり算」なんだ。
0のわり算のポイント
- 0このものを何人で分けたとしても、1人分は0こ。
(もともとないから、何人でわけても、「ない」) - 0をどんな数でわっても、答えは0になる。
0のわり算の練習
0÷4
0をどんな数でわっても、答えは0だから、
0÷4=0
0÷9
0をどんな数でわっても、答えは0だから、
0÷9=0
1で割るとどうなるのか?「1のわり算」
こんどは、1でわるとどうなるのか?を考える「1のわり算」について勉強していこう。
12このあめがあったとします。
次の人数で分けたら、1人分は何こになるかを考えてみましょう。
12このあめを4人で分ける
12このあめを4人で分けると、1人分は
12÷4=3こになるね。
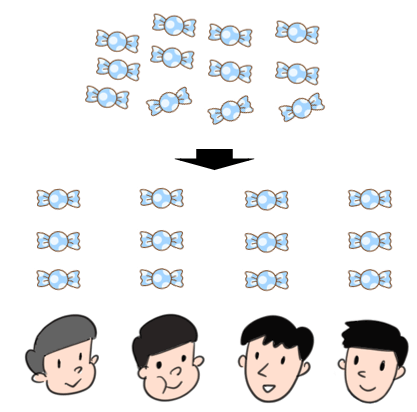
12このあめを3人で分ける
12このあめを3人で分けると、1人分は
12÷3=4こだね。
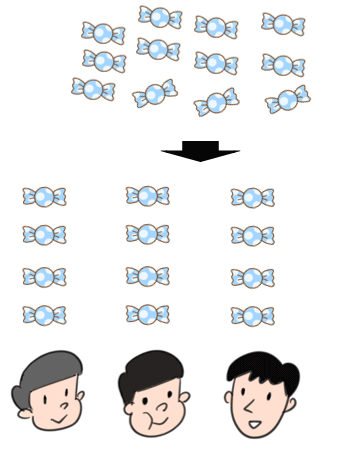
12このあめを2人で分ける
12このあめを2人で分けると、1人分は
12÷2=6こだね。
12このあめを1人で分ける
「1人で分ける」ということは、「全部自分のもの」にする、つまり「ひとりじめ」するということだよね。
だから1人分は12こになるね。
式で表わすと
12÷1=12となるよ。
この計算が、1でわる「1のわり算」なんだ。
1でわるということは、けっきょく、もとのまんまになるということなんだね。
1のわり算のポイント
- 1人で分けるということは、「全部自分のもの」「ひとりじめ」。
- 「わられる数」を「1」でわっても、答えは「わられる数」のまま。
1のわり算の練習
4÷1
「1」でわっても、答えは「わられる数」のままだから、
4÷1=4
4こを1人でわけても、1人分はそのまま4こだよね。
8÷1
「1」でわっても、答えは「わられる数」のままだから、
8÷1=8
8こを1人でわけても、1人分はそのまま8こだよね。
0で割ることができない理由
「0をわるとどうなるのか?」を考える、「0のわり算」を学習したね。
「0÷4」「0÷9」のように、「0」はいくつでわっても、答えは「0」だったね。
では、「4÷0」「9÷0」のように、「0」でわる計算はどうなるかな?
答えは
「計算できない」
だよ。
実は、算数の世界では、「0でわる」ことはゆるされていないんだ。
「なんで計算できないの?」とかんじた人もいるかな?
計算できないりゆうをかんたんにせつ明するね。
「0」でわれないりゆう
わり算って、そもそもどういうことかもういちど考えてみよう。
たとえば、8÷4=2だよね。
8÷4がいくつなのかをもとめるには、いちどかけ算の形にしてから、下の▢の部分にあてはまる数をさがせばよかったよね。

つまり、8÷4とは、「4にいくつをかけると、8になるのか?」を考えることなんだね。
では、「0でわるとどうなるのか」を考えてみるよ。
たとえば8÷0を考えてみよう。
さっきと同じように、かけ算の形にしてから、下の▢にあてはまる数をさがしてみるよ。

これって、「0にいくつをかけると、8になるのか?」ということなんだよね。
さっき、「0」には何をかけても「0」だと勉強したばかりだよね。
そう。「0」にかけたときに、「8」になる「ある数」なんてものはないよね。「0」には何をかけても「0」だからね。
でも、「0÷0」はどうだろう?
「0にいくつをかけると、0になるのか?」ということだったら、「0」には何をかけても「0」なのだから、「答えは何でもOK」になってしまうよね。
0ではない数を0でわるときは「答えがない」し、
0を0でわるときは、「答えは何でもOK」になってしまうんだ。
算数は、「○○を○○すると、○○になる」というルールがきちんと決まるかどうかが大切なんだ。
1+1は2と決まっていて、もしこれがときどき「3」だったり、「4」だったりしたら、それって算数ではなくなってしまうよね。
「答えがない」とか、「答えは何でもOK」なんてことは、算数ではゆるされないんだね。
だから、どんな数でも「0」でわることはできないんだ。
「0や1のわり算」まとめ
「0や1のわり算」まとめ
- 0をどんな数でわっても、答えは0になる。
- 「わられる数」を「1」でわっても、答えは「わられる数」のまま
- どんな数でも「0」でわることはできない
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。



