大きい数のわり算(2けた÷1けたのわり算)をわかりやすく解説
小学校3年生の算数で学習する「大きい数のわり算(2けた÷1けたのわり算)について、69÷3のような、おおきな数のわり算の考え方、こたえのもとめかたをわかりやすく解説するよ。
大きい数のわり算の考え方
2けた÷1けたのわり算のうち、「12÷3」のような、九九を使って答えをもとめることができるわり算なら、これまでに勉強してきたね。
「大きい数のわり算」では、「69÷3」のような大きい数のわり算が出てくるよ。
大きい数のわり算は、ふだんの生活でもつかう場面がよくあるよ。
たとえば、次のような場面。
- きゅうりが2本で88円だったとき、1本は何円だろう?
- 99円のおかしを3人でお金を出し合って買うばあい、1人は何円はらえばいいのかな?
電たくでも計算できるけれど、パッと計算できた方が便利だし、かっこいいよね。
「69÷3」は、どうやって答えをもとめたらよいだろう。
これまでのように九九を使って考えると、3の段は一番大きい数でも「3×9=27」だから、69÷3は大きすぎて答えをもとめることができないね。
大きい数のわり算をするときは、「位ごとにわけてわり算」すればいいんだよ!
さっそくやってみよう。
3こで69円のアメがあります。アメ1こはいくらですか。
3こで69円なのだから、1こ分のねだんをもとめるには「69÷3」を計算したらいいね。
図にすると次のようになるよ。

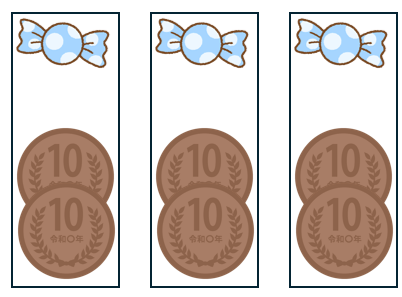
まずは十の位の「60円」に注目しよう。
60円を3こでわけるから、1こは60÷3=20円だよね。
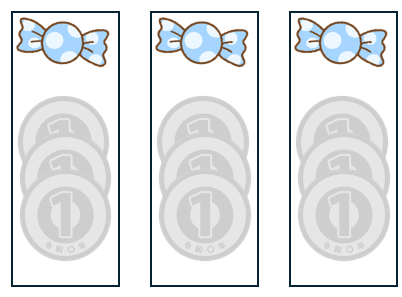
つぎに一の位の「9円」に注目しよう。
9円を3こでわけるから、1こは9÷3=3円になるよ。
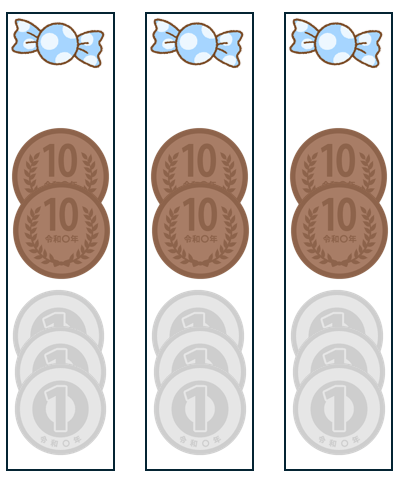
十の位のわり算でもとめた答えと、一の位のわり算でもとめた答えを合わせると、
20+3=23
アメ1このねだんは23円ともとめることができたね。
今、どういう風に計算したのかをおさらいしよう。
69を「60」と「9」にわけて、それぞれを「3」でわったんだよね。
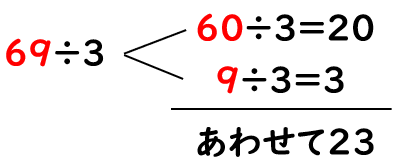
大きい数のわり算をするときは、位ごとにわけてから、わり算するといいね。
大きい数のかけ算(2けた×1けたのかけ算)のやり方と同じだね。
大きい数のわり算の練習
84÷2を計算しましょう。
84を位ごとにわけると、「80」と「4」だよね。
それぞれを「2」でわってみよう。

84÷2=42ともとめることができたね。
96÷3を計算しましょう。
96を位ごとにわけると、「90」と「6」だよね。
それぞれを「3」でわってみよう。
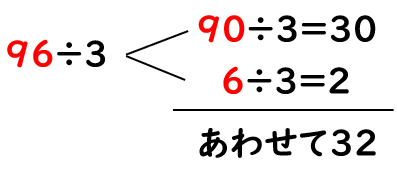
96÷3=32ともとめることができたね。
大きい数のわり算の文章問題
きゅうりが2本で88円で売られています。1本のねだんは何円ですか?
1本の値段をもとめるには、88÷2を計算したらいいね。
88を位ごとにわけると、「80」と「8」だよね。
それぞれを「2」でわってみよう。
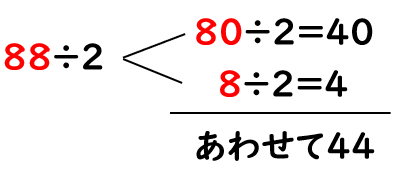
88÷2=44だから、きゅうり1本のねだんは44円ともとめることができたね。
99円のおかしを3人でお金を出し合って買います。1人は何円はらえばよいのかもとめましょう。
1人がはらうお金をもとめるには、99÷3を計算したらいいね。
99を位ごとにわけると、「90」と「9」だよね。
それぞれを「3」でわってみよう。
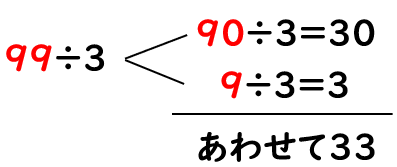
99÷3=33だから、1人33円はらえばいいともとめることができたね。
「大きい数のわり算(2けた÷1けたのわり算)」まとめ
「大きい数のわり算(2けた÷1けたのわり算)」まとめ
- 大きい数のわり算は、位ごとに数をわけて、それぞれをわる。
例:69÷3だったら、「60÷3」と「9÷3」にわけて計算する。
運営者情報

ゆみねこ
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。



