「かける数」と「かけられる数」文章問題からどっちか見分ける方法
小学校3年生の算数で学習する「かける数」と「かけられる数」について、「かける数とかけられる数」とはどういうことか、どっちが「かける数」でどっちが「かけられる数」なのかを見分ける方法をわかりやすく解説するよ。
文章問題から「かける数」と「かけられる数」を見つけられるようになろう!

「かける数とかけられる数」の問題に挑戦できる自動採点機能付きのドリルもあるよ!
ゆみねこドリル「かける数とかけられる数」のドリルページへ
「かける数」「かけられる数」とは
これまで、3×2=6のようなかけ算を勉強してきたね。
このとき、「かける数」とは、「3×2=6」のうちのどの数のことだろう?
そして、「かけられる数」とはどの数のことだろう?
どっちが「かける数」で、どっちが「かけられる数」かをきちんと りかいすることがとてもたいせつだよ。
「3×2=6」って、ことばでせつめいすると、
「3に2をかけると6になる」と言うことができるよね。
では、ここでアイスにチョコレートソースをかけたときを考えてみよう。
「アイスにチョコレートソースをかける」と言ったとき、「かけたもの」は何かな?
そう、「チョコレートソース」だよね。
では、チョコレートソースを「かけられたもの」は何かな?
そう、「アイス」だよね。
つまり、「かけるもの」は「チョコレートソース」で、
「かけられるもの」は「アイス」だよね。
ということは、「3に2をかける」とき、「かける数」は「2」だよね。
そして、「かけられる数」は「3」だよね。
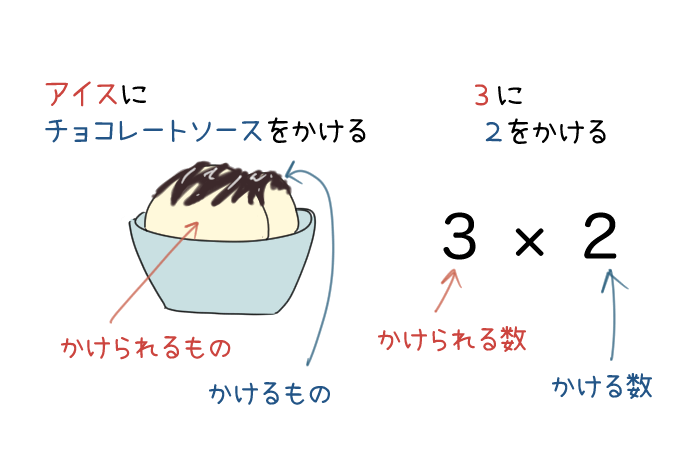
○×△の式があったとき、はじめにある「○」が「かけられる数」で、かけるの記号のあとにくる「△」が「かける数」だよ。
「かける数」と「かけられる数」の順ばんの考えかた
「かける数」と「かけられる数」の見わけかたはわかったかな。
では、こんどは「文しょう問題」からどうやって「かける数」と「かけられる数」を見つけたらよいかを考えてみよう。
あめを2こずつ、5人の子どもにくばります。あめはいくつひつようですか。
問題を読んで、「かけ算をする」ということはわかるね。
でも、この問題では、どれが「かける数」で、どれが「かけられる数」なのかわかるかな??
「かける数」と「かけられる数」を見わけるには、式にすればわかるよね。
でも、問題には式も書いていないから、自分で考えなくてはいけないよね。
式にするとき、「あめを2つ」の「2」と、「5人の子ども」の「5」、どちらを先にすればいいのだろう??
つまり、「2×5」なのか、「5×2」なのか、どっちが正しいのかな?ということだね。
求めるものが何か?で見わけよう
じつは、見わけるためのとってもカンタンな目じるしがあるんだ。
それは、問題のさい後に聞かれる、「何をもとめるのか」ということば。
たとえば、この問題では、さい後に「あめはいくつひつようですか」と聞いているよね。
つまり、「求めるのは、あめの数」なんだよね。
このとき、かけ算の式は「あめの数」を先にするんだ。
だから、「あめを2つ」の「2」がいちばんはじめになるんだよ。
つまり「2×5」という式が正しいんだ。
ということは、「2」が「かけられる数」で、「5」が「かける数」なんだね。
でも、「かけざんのきまり」で考えると、「2×5」も「5×2」も、こたえは同じ「10」だよ。
順ばんってそんなにだいじなの?
たしかに、どちらの式も、求められるこたえは同じになるね。
でも、テストなどでは、問題文から式も考えて書かなければいけないこともあって、その時に「かける数」と「かけられる数」の順ばんがまちがっていると、不せいかいとか、△になってしまうばあいがあるよ。
つまり、かけ算というのは、「何を求めるためにかけ算をするのか」ということをおさえているかどうかが、だいじだということだね。
たとえば、「あめの数をもとめる問題」でもういちど考えてみて。
「子ども一人に2つずつあめをくばる」とき、もし子どもが1人だったら、あめは「2こ」でいいよね。
子どもが2人だったら、「2+2」だよね。
子どもが3人だったら、「2+2+2」だよね。
子でもが4人だったら、「2+2+2+2」だよね。
そして子どもが5人だったら、「2+2+2+2+2」だよね。
これって、「2」がいくつひつようか、を考えているんだよね。
子どもが5人だと、「2」が「5」つひつよう、ということだよね。
「かけ算」って、もとは「たし算」なんだよ。
でも、「おなじ数をずっとたす」ときは、いちいち「2+2+2+・・・・」としていくよりも、「2×○」というように、「2が○こあると、△になるよ」というのをすぐ求められるようにしているんだよね。
それで、すぐにこたえを求められるように、1から9までの「□が○こあると、△になる」というのをおぼえてしまうのが、かけ算の九九なんだ。
だから、あめの問題は、「2こ」のあめがいくつひつようか?がもとにあって、それが「5人」だから、「2+2+2+2+2」をけい算するために、「2×5」をするんだ。
もし式を「5×2」にしてしまうと、それって「5+5」ということだよね。
「5人の子どもが2組み」ということになってしまうよね。
それって、問題のないようとちがうよね。
「かける数」と「かけられる数」の順ばんの考えかた
問題のさい後に聞かれる、「何を求めるのか」ということばに ちゅうもくしよう。
(例)
「あめはいくつひつようですか?」→あめの数をあらわす数がさきにくる
「かける数」の求め方
「かける数」と「かけられる数」とはどういうことかわかったかな。
こんどは、かけ算の式で「かける数」と「かけられる数」がいくつかわからないときに求めるやり方をしょうかいするよ。
テストでは、つぎのような問題が出るんだ。
8×▢=48という式から、▢に入る数字を求めましょう。
▢は、「かける数」だったよね。
8に何をかけたら、48になるかを求めればいいんだね。
「九九の表で考える方ほう」と「九九をつかって▢にじゅんばんに当てはめる方ほう」をしょうかいするね。
「かける数」を九九の表で考える
九九の表には、1から9までの数をそれぞれかけると、いくつになるかがまとめられているよね。
「8に何をかけたら48になるか」をさがすには、かけられる数が「8」で答えが「48」になっているところをかくにんすればいいね。
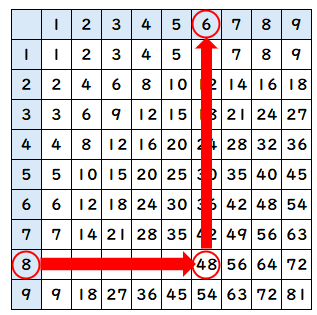
九九表でかくにんすると、かける数は「6」と求めることができるたね。
「8×▢=48」の▢には「6」が入るね。
▢にじゅんばんにあてはめて「かける数」をさがす
九九表がなくても、九九をぜんぶ言えるようになっていれば、ひとつずつあてはめていって さがすことができるよ。
「8×▢=48」の▢に、数字を1から9までじゅんばんにあてはめてみるよ。
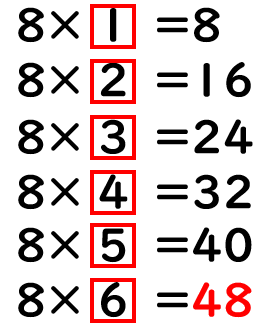
6まで かくにんしたところで、こたえが48になったね。
なので「8×▢=48」の▢には「6」が入るとわかるね。
「かけられる数」の求め方
こんどは「かける数」ではなく、「かけられる数」を求めていくよ。
やり方は「かける数」を求めるときと同じだよ。
▢×9=36という式から、▢に入る数字を求めてみよう。
「かけられる数」を九九の表で考える
かける数が「9」で答えが「36」のところをかくにんすれば、
かけられる数は「4」と求めることができるね。
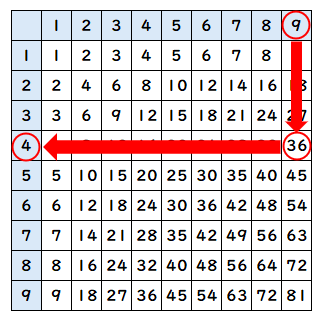
だから、「▢×9=36」の▢には「4」が入るとわかるね。
▢にじゅんばんにあてはめて「かけられる数」をさがす
「▢×9=36」の▢に数字を1から9までじゅんばんにあてはめてみるよ。
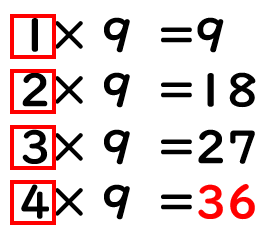
4まで かくにんしたところで、こたえが36になったね。
なので「▢×9=36」の▢には「4」が入るとわかるね。
「かける数」と「かけられる数」を求める練習問題
つぎの▢にあてはまる数をこたえましょう。
(1)▢×6=30
(2)8×▢=24
(1)▢×6=30
九九の表を見て考えると、次のようになるよ。
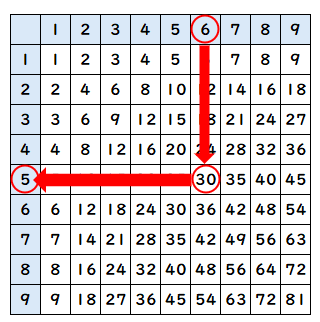
「▢×6=30」の▢には「5」が入るとわかるね。
(2)8×▢=24
九九をつかって、▢に数をじゅんばんに当てはめてみよう。
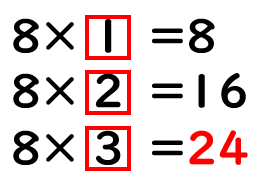
「8×▢=24」の▢には「3」が入るとわかるね。
「かける数」と「かけられる数」まとめ
「かける数」と「かけられる数」まとめ
- ○×△の式があったとき、はじめにある「○」が「かけられる数」で、かけるの記号のあとにくる「△」が「かける数」である。
- 文章問題から「かける数」と「かけられる数」を考えるには、問題のさい後に聞かれる、「何を求めるのか」ということばに ちゅうもくしよう。
求めるものが、「かけられる数」だよ。 - かける数とかけられる数を求めるには、「九九の表で考える方ほう」と「▢にじゅんばんに数字を当てはめていく方ほう」がある。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。



