「わられる数」と「わる数」(何人に分けられるかをもとめる計算)
小学校3年生の算数で学習する「何人に分けられるかをもとめる計算」について、「わられる数」と「わる数」とはなにか、どっちがどっちかの見分け方、何人にわけられるかをもとめる計算のやり方をわかりやすく解説するよ。
「わられる数」と「わる数」とは
まずはじめに、わり算でつかう言葉をおぼえておこう。
かけ算のときも、「かける数」と「かけられる数」というのがあったよね。
「3×4」だったら、
「3」がかけられる数で、「4」がかける数だったよね。
わり算でも考えかたはおなじ。
「12÷3」という式があったら、
「12」のことをわられる数、「3」のことをわる数というよ。

この「わられる数」と「わる数」は、どっちがどっちだったかな?と、ときどきわからなくなってしまう子も多いんだ。
そんなときは、12÷3の式をことばでせつめいしてみよう。
ことばであらわすと、「12を3でわる」と言うことができるよね。
「ボールを足でける」を考えてみて。
「けられるもの」は「ボール」だよね。
「けるもの」は「足」だよね。
これとおなじ。
「12を3でわる」のだから、
「わられる数」は「12」だよね。
「わる数」は「3」だよね。
わり算の式をことばであらわしてみると、「わられる数」と「わる数」がハッキリするよ。
何人に分けられるかをもとめる計算「わり算」
1人分の数をもとめる計算の学習では、1人分の数をもとめるには、「わり算」を使えばよいということを学んだね。
たとえば、「30こ」を「5人で分ける」とき、
1人分は「30÷5」という式で書くことができたね。
今回は、「何人で分けることができるか」をもとめる計算について考えるのだけれど、答えから言ってしまうと、「何人で分けることができるか」をもとめる計算も、「わり算」を使うんだ。
「何人に分けられるかをもとめる」計算がひつようになる場面は次の通りだよ。
- あめが12こあるとき、1人3こずつ分けると、何人に分けられるか。
- おりがみが28まいあるとき、1人4まいずつ分けると、何人に分けられるか。
- 27cmのひもを、1人3cmずつ分けると、何人に分けられるか。
こんなかんじで、何人にわけられるかをもとめる場面はよくあるんだ。
では、じっさいにどうやってもとめるかを かくにんしていこう。
何人に分けられるかをもとめる計算①
あめが12こあるとき、1人3こずつ分けると、何人に分けられますか。

図で考えてみよう。
次のように12このあめを3こずつ分けたら、4人に分けられることが分かるね。
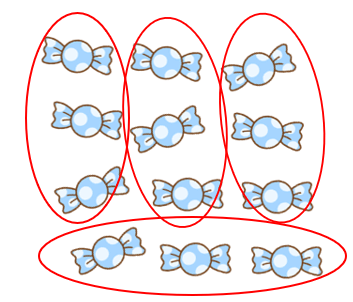
これを式にすると、
12÷3=4
(読み方:12わる3は4)
と表すことができるね。
何人に分けられるかを図で考えることができたね。
でも、もしあめの数が多かったら、図で考えるのはたいへんだよね。
だから式だけでももとめてみよう。
何人に分けられるかを、かけ算の九九を使って予想してみるよ。
もし1人に分けたら
1人3こずつ分けるのだから、1人に分けたら、3×1=3こになるよね。
→あめは12こあるんだよね。これではあめがあまってしまうよ。
12こにならないから、「1人にわける」はまちがっているよ。
2人に分けたら
1人3こずつだから、2人いたら、3×2=6こになるよね。
→12こにならないから、まちがっているよ。
3人に分けたら
1人3こずつだから、3人いたら、3×3=9こになるよね。
→12こにならないから、まちがっているよ。
でもだんだん近づいてきたね。
4人に分けたら
1人3こずつだから、4人いたら、3×4=12こになるよね。
→あめの数とおなじ12こになったから、4人が答えだよ。
いま、ひたすら考えたことは
下の▢にあてはまる数は何が入るかなと予想したことよ。
「1人分の数をもとめる」ときとおなじだね。

「3に、何をかけると12になるだろう?」ということを考えたんだったね。かけ算の九九をつかって、▢にじゅん番に数字を入れてたしかめていくと、3にかけると12になるのは、「4」ということが分かったね。
だから、▢にあてはまる数は「4」が答えだね。
12÷3を計算するには、「わる数(3)」に何をかけると「わられる数(12)」になるかを、九九で考えればいいんだね。

何人に分けられるかをもとめる計算②
おりがみが28まいあるとき、1人4まいずつ分けると、何人に分けることができますか。

28まいのおりがみを4まいずつわけたら、7人に分けられるね。

これを式にすると、
28÷4=7
(28わる4は7)
と表すことができるね。
何人に分けられるかを予想して、かけ算の九九をつかって式だけで もとめてみよう。
1人に分けたら
1人4まいずつ分けるのだから、1人に分けたら、4×1=4まいになるよね。
→28まいにならないから、まちがっているよ。
2人に分けたら
1人4まいずつ分けるのだから、2人に分けたら、4×2=8まいになるよね。
→28まいにならないから、まちがっているよ。
これをつづけていくと
7人に分けたら
1人4まいずつ分けるのだから、7人に分けたら、4×7=28まいになるよね。
→おりがみの数の28まいとおなじになったね。なので、7人が答えだよ。
いま、ひたすら考えたことは
下の▢にあてはまる数は何が入るかなと予想したことだったよね。

「4に、何をかけると28になるだろう?」ということを考えたんだったね。
かけ算の九九をつかって、▢にじゅん番に数字を入れてたしかめていくと、4にかけると28になるのは、「7」ということがわかったね。
だから、▢にあてはまる数は「7」が答えだね。
28÷4を計算するには、「わる数(4)」に何をかけると「わられる数(28)」になるかを、九九で考えればいいんだね。

何人に分けられるかをもとめる計算③
27cmのひもを、1人3cmずつわけると、何人で分けられますか。
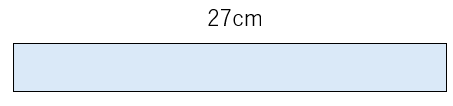
27cmのひもを、3cmずつわけたら、9人に分けられることがわかるね。
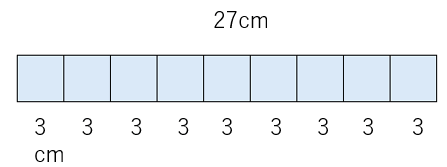
これを式にすると、
27÷3=9
(27わる3は9)
と表すことができるね。
何人に分けられるかを予想して、かけ算の九九をつかって式だけで もとめてみよう。
1人に分けたら
1人3cmずつだから、1人に分けたら、3×1=3cmになるよね。
→27cmにならないから、まちがっているよ。
2人に分けたら
1人3cmずつだから、2人に分けたら、3×2=6cmになるよね。
→27cmにならないから、まちがっているよ。
これをつづけていくと、
9人に分けたら
1人3cmずつだから、9人に分けたら、3×9=27cmになるよね。
→ひもの長さとおなじ27cmになったから、9人が答えだよ。
いま、ひたすら考えたことは
下の▢にあてはまる数は何が入るかなと予想したことだったね。

かけ算の九九をつかって、▢にじゅん番に数字を入れていくと、「9」が答えだとわかったね。
27÷3を計算するには、「わる数(3)」に何をかけると「わられる数(27)」になるかを、九九で考えればいいんだね。

わり算の練習問題
わり算をするときには、わる数のだんの九九を使えば答えを見つけるというポイントを使って、わり算の練習をしていこう。
18÷3
わる数は「3」だよね。
3のだんの九九で「18」になる数を見つけよう。
3×1=3
3×2=6
・・・・
3×6=18
だから、18÷3=6だよ。
36÷9
わる数は「9」だよね。
9のだんの九九で「36」になる数は「4」だね。
だから、36÷9=4だよ。
54÷6
わる数は「6」だよね。
6のだんの九九で「54」になる数は「9」だね。
だから、54÷6=9だよ。
24このボールを6こずつかごに入れると、かごはいくつひつようですか。
「何人いるか」をもとめる問題ではないけど、
同じように考えることができるよ。
24このボールを6こずつわけるってことだから、
24÷6という式でもとめられるね。
「24÷6」のわる数は「6」だよね。
6のだんの九九で「24」になる数は「4」だから、24÷6=4。
かごは4こひつようだとわかるね。
「何人に分けられるかをもとめる計算」まとめ
何人に分けられるかをもとめる計算のやり方
- 「何人に分けられるかをもとめる」ときも、「1人分の数をもとめる」ときも、わり算を使って計算したらよい。
- わり算をするときには、わる数のだんの九九を使えば答えを見つけられる。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


