「分数とわり算」分数とわり算の関係と求め方をわかりやすく解説
小学校3年生の算数で学習する「分数とわり算」について、分数とわり算にはどういうかんけいがあるのか、ある数の分数をもとめるために、わり算をどう使えばよいのか、分数とわり算のかんけいを使って、長さを比べたりする問題の解き方をわかりやすく解説するよ。
「分数とは」(2年生のふくしゅう)
「分数」というのは、下の図のように

というような形で表すことができる数のことだよ。
分数の「〇」や「▢」の部分には数字が入るよ。
2年生の算数では、\(\frac{1}{2}\)と\(\frac{1}{4}\)という分数について勉強したよね。
\(\frac{1}{2}\)と\(\frac{1}{4}\)とは、どういうことだったか おさらいしよう。
- 「\(\frac{1}{2}\)」とは、「2つに分けた」うちの「ひとつ分」のこと。
だから「2ぶんの1」と読むんだったね。 - 「\(\frac{1}{4}\)」とは、「4つに分けた」うちの「ひとつ分」のこと。
だから「4ぶんの1」と読むよね。
「分数」と「わり算」のかんけい
「分数」と「わり算」は、すごくにているんだ。
どんなところがにているのかを しょうかいしていくね。
60cmの\(\frac{1}{2}\)の長さは何cmだろう?
\(\frac{1}{2}\)というのは、「2つに分けた」うちの「ひとつ分」のことだから、60cmの\(\frac{1}{2}\)は30cmだとわかるね。
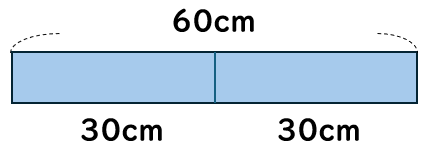
これは、次のようにも考えることができるよね。
60cmを2等分した(2でわった)1こ分の長さだから、60÷2=30cm。
「\(\frac{1}{2}\)」と「2でわる」はおなじことなんだね!
80cmの\(\frac{1}{4}\)の長さは何cmだろう?
\(\frac{1}{4}\)というのは、「4つに分けた」うちの「ひとつ分」のことだから、80cmの\(\frac{1}{4}\)は20cmだとわかるね。
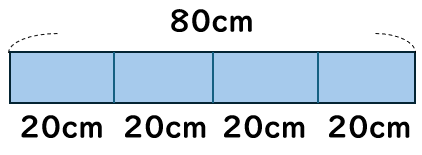
これも、次のようにも考えることができるよね。
80cmを4等分した(4でわった)1こ分の長さだから、80÷4=20cm。
「\(\frac{1}{4}\)」も、「4でわる」とおなじことなんだね。
もう1つたしかめてみよう。
90cmの\(\frac{1}{3}\)の長さは何cmだろう?
\(\frac{1}{3}\)というのは、「3つに分けた」うちの「ひとつ分」のことだから、90cmの\(\frac{1}{3}\)は30cmだとわかるね。
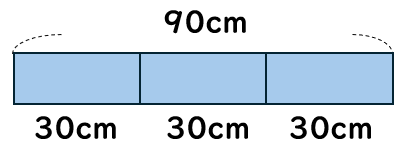
これも次のようにも考えられるよね。
90cmを3等分した(3でわった)1こ分の長さだから、90÷3=30cm。
「分数」と「わり算」はすごくにていることがわかったかな?
言い方はちがうけれど、もとめるための考え方がおなじなんだね。
「分数」と「わり算」のかんけい
- 60cmの\(\frac{1}{2}\)と、60÷2は同じ答えになる。
- 80cmの\(\frac{1}{4}\)と、80÷4は同じ答えになる。
- 90cmの\(\frac{1}{3}\)と、90÷3は同じ答えになる。
ある数の分数をもとめる
この「分数」と「わり算」のかんけいがわかったら、「ある数の分数がいくつになるか」ももとめられるようになるよ。
たとえば、93cmの\(\frac{1}{3}\)は何cmになるかな?
「93cmの\(\frac{1}{3}\)」と、「93÷3」は同じ答えになるよね。
だから、93÷3を計算してみよう。
前回、大きい数のわり算を勉強したよね。
93÷3は、93を「90」と「3」にわけて、それぞれを「3」でわればよかったね。
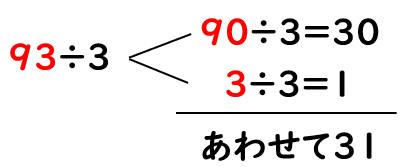
93÷3=31だから、
93cmの\(\frac{1}{3}\)は31cmだともとめることができるよ。
分数とわり算の問題(長さをくらべる)
分数とわり算のかんけいを使って、長さをくらべる問題にちょうせんしてみよう。
48cmと、44cmのテープがあります。
2つのテープのそれぞれ\(\frac{1}{4}\)の長さは、どちらが長いのかくらべましょう。
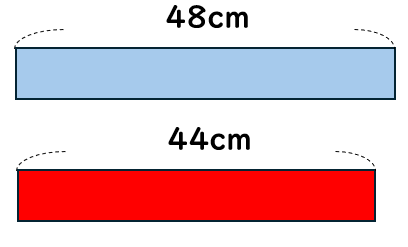
青のテープの\(\frac{1}{4}\)の長さをもとめよう。
48cmの\(\frac{1}{4}\)だから、
48÷4を計算したらいいよね。
48を「40」と「8」にわけて、それぞれを「4」でわってみよう。
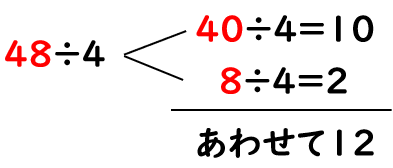
48÷4=12だから、
48cmの\(\frac{1}{4}\)は12cmだとわかるよ。
赤のテープの\(\frac{1}{4}\)の長さをもとめよう。
44cmの\(\frac{1}{4}\)だから、
44÷4を計算したらいいよね。
44を「40」と「4」にわけて、それぞれを「4」でわってみよう。
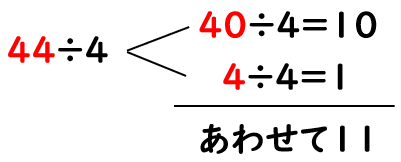
44÷4=11だから、
44cmの\(\frac{1}{4}\)は11cmだとわかるよ。
2つのテープの\(\frac{1}{4}\)の長さは
青が12cm、赤が11cmで、青のテープの方が長いことがわかるね。
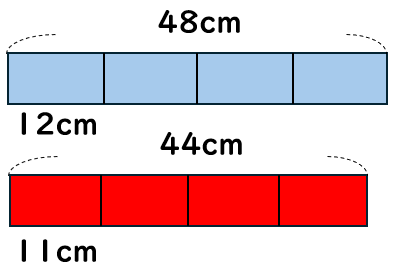
どちらも\(\frac{1}{4}\)にするなら、もとの長さが青のテープの方が長いのだから、\(\frac{1}{4}\)した長さも青のテープの方が長くなるよね。
長さをくらべる問題
次の➀と➁は、どちらの長さが長いかもとめましょう。
①36cmの\(\frac{1}{3}\) ②44cmの\(\frac{1}{4}\)
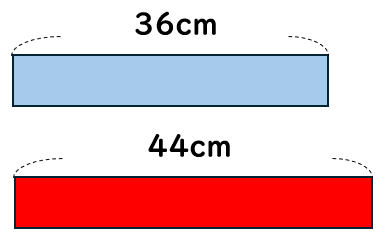
もとのテープの長さは44cmの方が長いけれど、こんどはそれぞれの分数が違うね。
どうなるか、じっさいに計算してみよう。
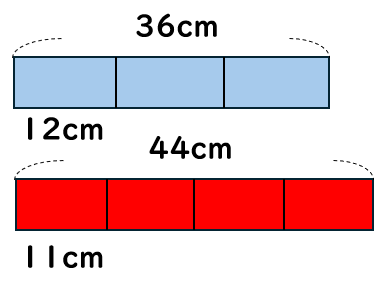
①36cmの\(\frac{1}{3}\)をもとめるよ。
36÷3を計算すると「12」になるから、
36cmの\(\frac{1}{3}\)は12cmだよ。
②44cmの\(\frac{1}{4}\)をもとめるよ。
44÷4を計算すると「11」になるから、
44cmの\(\frac{1}{4}\)は11cmだよ。
➀と➁をくらべると、44cmの\(\frac{1}{4}\)よりも36cmの\(\frac{1}{3}\)の方が長いことがわかるね。
「分数とわり算」まとめ
分数で考えるのがむずかしいときは、わり算に直して考えることができる。
- 60cmの\(\frac{1}{2}\)と、60÷2は同じ答え
- 80cmの\(\frac{1}{4}\)と、80÷4は同じ答え
- 90cmの\(\frac{1}{3}\)と、90÷3は同じ答え
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。




とても分かりやすくて助かりました!!