「あまりのあるわり算」の考え方とやり方をわかりやすく解説
小学校3年生の算数で学習する「あまりのあるわり算」について、あまりのあるわり算とはどういうことか、あまりのあるわり算の計算のやり方をわかりやすく解説するよ。
あまりのあるわり算の練習問題や、まちがえやすいこと、たしかめのやり方も紹介しているよ。
「あまりのあるわり算」とは
これまでに、「16÷4」や「24÷6」のようなわり算を勉強したきたよね。
じつは、これらは「あまりのないわり算」なんだ。
16÷4は、「4×4」をすればピッタリ16になるから答えは「4」だし、
24÷6も、「6×4」をすればピッタリ24になって、答えが「4」だともとめることができたよね。
このように、ピッタリ計算ができて、ピッタリ答えがもとめられるものが「あまりのないわり算」だよ。
では、「あまりのあるわり算」とはどういうことかな?
あまりのあるわり算のたとえをしょうかいするね。
あまりのあるわり算①
17このあめを4人で分けると、1人何こになって、何こあまるかをもとめましょう。
17このあめを4人で分けてみよう。
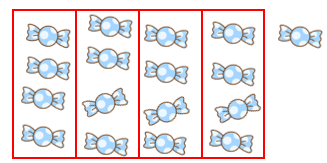
1人に4こずつくばったところで、残りが1こだけになってしまって、もうくばることができなくなっちゃった。
そう、あめは1人4こずつになって、1こだけあまるよね。
これが「あまりのあるわり算」なんだ。
このときの式は「17÷4=4あまり1」と書くよ。
あまりのあるわり算②
38このあめを4人で分けると、1人何こになって、何こあまるかをもとめよう。
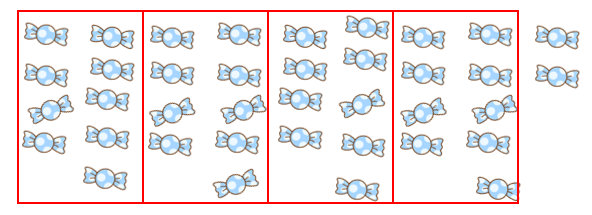
あめは1人9こずつになって、2こあまるよね。
これも「あまりのあるわり算」だね。
このときの式は「38÷4=9あまり2」と書くよ。
なるほど、何人かでわけるときに、ピッタリきれいにくばれるとはかぎらないよね。
それが「あまりのあるわり算」なんだね。
このように、わり算をするときに、あまりがあるときは「わりきれない」といって、
あまりがないときは「わりきれる」というよ。
「わりきれない」わり算とは
あまりがあるわり算のこと
例:17÷4=4あまり1、38÷4=9あまり2
「わりきれる」わり算とは
あまりがないわり算のこと
例:16÷4=4、36÷9=4
「あまりのあるわり算」の計算のやり方
「あまりがあるわり算」とはどういうことかがわかったかな。
それでは、あまりのあるわり算はどうやって計算するのかをしょうかいしていくね。
まずは「あまりのないわり算」はどうやって計算してきたのか、おさらいしよう。
たとえば「20÷4」だったら、
20÷4のわる数は「4」だから、4のだんの九九で「20」になる数を見つければよかったね。
4×1=4
4×2=8
4×3=12
4×4=16
4×5=20!!
4×5が20になるので、20÷4の答えは「5」だともとめることができるね。
では、あまりがあるわり算の場合はどうやって計算したらいいのかな?
38÷9をわり算してみよう。
38÷9のわる数は「9」だから、
9のだんの九九で「38」になる数をさがしてみよう。
9×1=9
9×2=18
9×3=27
9×4=36
9×5=45
あれ・・・?
9のだんの九九で「38」になる数はないね。
そう、「あまりのあるわり算」は、わられる数が九九の答えにないんだ。
しかたがないので、わられる数に近くて、それよりも少ない九九の答えをさがそう。
わられる数「38」にできるだけ近くて、それよりも少ないのは「9×4=36」だよね。
さがせたら、「36」を、わられる数「38」からひいて、あまりをもとめよう。
38-36=2
あまりは「2」になるね。
38÷9=4あまり2が答えだよ。
あまりのあるわり算の計算のやり方
- 「わる数」の九九をつかって考える。
- わられる数に近くて、それよりも少ない九九の答えをさがす。
- さがした答えを、わられる数からひいて、あまりをもとめる。
「あまりのあるわり算」の練習問題
それでは、「あまりのあるわり算」をじっさいにやってみよう。
40÷7をわり算してみよう。
40÷7のわる数は「7」だから、
7のだんの九九で「40」になる数を見つけよう。
7×1=7
7×2=14
7×3=21
7×4=28
7×5=35
7×6=42
7のだんの九九で「40」になる数はないね。
ということは、「あまりがあるわり算」だということだよ。
わられる数に近くてそれより少ない九九の答えをさがそう。
「7×6=42」だと、わられる数「40」よりも大きくなってしまうから、
「7×5=35」が答えになるよ。
答えをさがせたら、あまりをもとめよう。
35を「わられる数40」からひいて、あまりが「5」ともとめられるね。
40÷7=5あまり5が答えだよ。
51÷6をわり算してみよう。
51÷6のわる数は「6」だから、
6のだんの九九で「51」になる数を見つけよう。
6×6=36
6×7=42
6×8=48
6×9=54
6のだんの九九で「51」になる数はないね。
ということは「あまりがあるわり算」ということだね。
わられる数に近くてそれより少ない九九の答えをさがして、九九の式を予想するよ。
「6×9=54」では51よりも大きくなってしまうから、
「6×8=48」が答えになるよ。
あとは、あまりをもとめよう。
48を「わられる数51」からひいて、あまりは「3」ともとめられるね。
51÷6=8あまり3が答えだよ。
41このあめを6人でわけたら、1人分は何こになって、何こあまりますか。
今回は文章題だね。
41このあめを6人でわけたときの、1人分の数をもとめるから、「41÷6」を計算したらいいね。
41÷6はあまりがあるわり算だから、
6のだんの九九で、わられる数に近くてそれより少ない答えをさがすと、
6×6=36
36を41からひいて、あまり5
41÷6=6あまり5となるから、
41このあめを6人でわけたら、1人分は6こで、5こあまるとわかるね。
「あまりのあるわり算」でまちがえやすいこと
さっきと同じ計算を考えてみよう。
ただ、わざとまちがえた計算をしているよ。
41このあめを6人でわけたら、1人分は何こになって、何こあまりますか。
41÷6を計算したらいいね。
41÷6はあまりがあるわり算だったから、
6のだんの九九で、わられる数に近くてそれより少ない答えをさがすと、
6×5=30(ここをわざとまちがえているよ。本当は6×6=36だよね。)
30を41からひいて、あまり11
だから、41÷6=5あまり11
41このあめを6人でわけたら、
1人分は5こで、11こあまるともとめられるね。
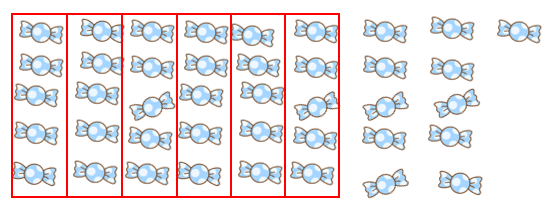
ただ、これってすごくおかしいよね。
11こあまるってことは、まだ6人でわけることができそうだよね。
あまりのあるわり算で、答えがもとまったら、「あまり」を見よう。
「あまり」が「わる数」より大きかったら、まだ、わけられるということだよ。
「あまりのあるわり算」の計算で気をつけること
「あまり」が「わる数」より小さくなっているか?を、かくにんしよう。
「あまり」が「わる数」よりも大きかったら、まだわけられるよ。
「あまりのあるわり算」たしかめのやり方
あまりのあるわり算で、「もとめた答えが正しいかどうか」をたしかめるやり方をしょうかいするね。
次の2つの計算で正しいものはどっちでしょうか。
①23÷6=3あまり5
②23÷6=4あまり1
図でたしかめるやり方
①と②の式を、「あめをわけたとき」の図で考えてみるよ。
①は、「23このあめを6人でわけたら、1人分は3こで、5こあまった。」ということになるよね。
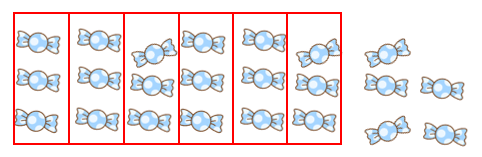
②は、「23このあめを6人でわけたら、1人分は4こで、1こあまった。」ということになるけれど・・・
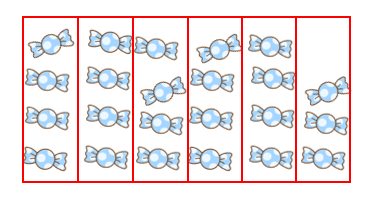
図でたしかめてみると、「1こあまった」のではなくて、「1人だけ3こしかない人がいる(1こたりない)」ことがわかるよね。
だから、①が正しいことがわかるね。
ただ、図でたしかめるのはすこし大変だね。
あまりのあるわり算は、式だけでたしかめるやり方もあるんだ。
式でたしかめるやり方
「23÷6=3あまり5」をもとめるには、
6×3=18をさがして、
23-18=5をしたんだよね。
つまり、「23は、6×3に5をたしたもの」ということなんだ。
「23÷6=3あまり5」という式は、「23=6×3+5」と言いかえることができるんだね。
だから、わり算の式の記号は次のようにかえて考えることができるんだ。
「÷」→「=」
「=」→「×」
「あまり」→「+」
記号をかえたときに、その式が正しいかどうかで、あまりのあるわり算の式をたしかめてみよう。
➀「23÷6=3あまり5」→「23=6×3+5」だから、正しいね。
➁「23÷6=4あまり1」→「23=6×4+1」
これは、正しくないよね。
なぜなら、6×4+1=25だからね。
あまりのあるわり算の答えをもとめたら、式の記号をかえて、正しいかどうかをたしかめるとあんしんだね。
「あまりのあるわり算」のまとめ
「あまりのあるわり算の計算のやり方」まとめ
- あまりがあるわり算は、わりきれない。
- わる数の九九をつかって考える。
- わられる数に近くてそれより少ない九九の答えをさがしてから、わられる数からひいて、あまりをもとめる。
- 答えがもとまったら、「あまり」を見よう。「あまり」が「わる数」より小さくなっているかをかくにんしよう。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。




