「割り算」とは?やり方をわかりやすく解説(1人分を求める計算)
小学校3年生で学習する「わり算」について、1人分を求める計算「わり算」とはどういうことか、わり算のやり方をわかりやすく解説するよ。
わり算の答えの求め方を、練習問題も紹介しながらくわしく説明しているよ。
1人分の数をもとめる計算「わり算」
「1人分は、いくつになるだろう?」
を考える場面ってあるよね。たとえば・・
- あめが12こあるとき、3人でわけると1人分はいくつ?
- おりがみが28まいあるとき、4人でわけるときの1人分は何まい?
- 27cmのひもを9人でわけると、1人分は何cm?
このように、「1人分の数をもとめる」場面はよくあるんだ。
1人分の数をもとめるには「わり算」という計算を使うよ。
今まで、「たし算」「ひき算」「かけ算」を勉強してきたよね。
さい後に登場するのが「わり算」なんだ。
※ちなみにこの4つを「四則演算(しそくえんざん)」と言うよ。
ただ、「わり算」はかけ算の九九が全部言えるようになっていれば、だいじょうぶ。むずかしいことはないよ。
生活の場面でもわり算を使うことは多いから、しっかりできるようになっておこう。
では、じっさいにどうやってもとめるかをかくにんしていくね。
1人分の数をもとめる計算「わり算」①
あめが12こあるとき、3人でわけると1人分は何こになりますか。

図で考えてみよう。
3人が同じ数になるようにわけたら、1人分は4こだとわかるね。
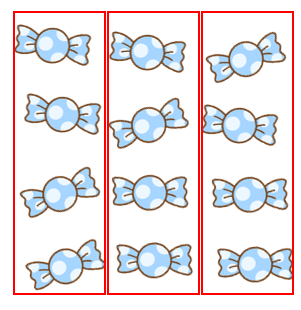
これを式にすると、
12÷3=4
(読み方:12わる3は4)
と表すことができるんだ。
ここではじめて登場した「÷」を大きく書いてみよう。
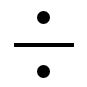
これが「わり算」を表す記号だよ。
書きじゅんは、①真ん中の横線→②上の点→③下の点のじゅん番だよ。
1人分の数をもとめる計算「わり算」②
おりがみが28まいあるとき、4人でわけると1人分は何まいになりますか。

4人が同じ数になるようにわけたら、1人分は7まいだとわかるね。
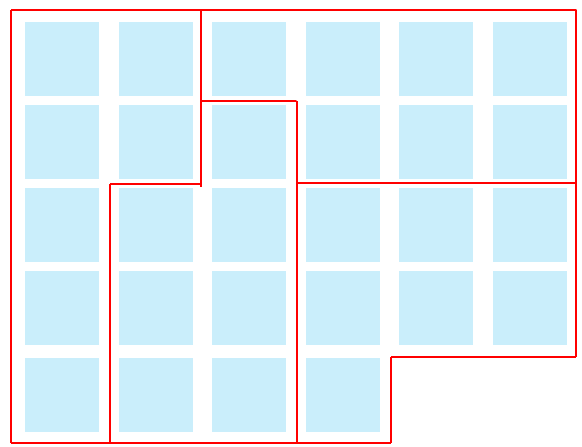
これを式にすると、
28÷4=7
(28わる4は7)
と表すことができるんだ。
1人分の数をもとめる計算「わり算」③
27cmのひもを9人でわけると、1人分は何cmになりますか。
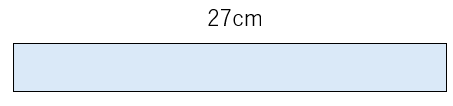
9人が同じ数になるようにわけたら、1人分は3cmだとわかるね。
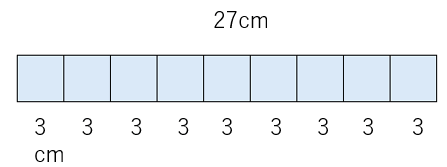
これを式にすると、
27÷9=3
(27わる9は3)
と表すことができるんだ。
わり算の計算のやり方
ここまでは、図を使って1人分の数を求めてきたね。
ただ、いちいち図を書かなくちゃいけないから大へんだよね。
もし、「81こを9人でわける」という問題がでたら、「81この図なんて書けないよ!」ってなるよね。
実は、わり算には計算のやり方があるんだ。
これを知っておけば図を書かくなくても計算でもとめることができるんだ。
次の問題を考えてみよう。
あめが81こあるとき、9人でわけると1人分は何こになりますか。

式にすると、
81÷9
というわり算の式になるよ。
9人が同じ数になるようにわければいいんだけれど、この問題を図で考えるのはむずかしそうだね。
そこで、1人分のあめの数を予想してみよう。
このときに、「かけ算の九九」をつかうよ。
もし1人分を1こにしたら
9人いるから、全部のあめの数は1×9=9こになるよね。
→あめは81こあるんだよね。
81こにならないから、「1人分が1こ」はまちがっているよ。
1人分を2こにしたら
9人いるから、全部のあめの数は2×9=18こになるよね。
→81こにならないから、まちがっているよ。
1人分を3こにしたら
9人いるから、全部のあめの数は3×9=27こになるよね。
→81こにならないから、まちがっているよ。
1人分を4こにしたら
9人いるから、全部のあめの数は4×9=36こになるよね。
→81こにならないから、まちがっているよ。
1人分を5こにしたら
9人いるから、全部のあめの数は5×9=45こになるよね。
→81こにならないから、まちがっているよ。
1人分を6こにしたら
9人いるから、全部のあめの数は6×9=54こになるよね。
→81こにならないから、まちがっているよ。
1人分を7こにしたら
9人いるから、全部のあめの数は7×9=63こになるよね。
→81こにならないから、まちがっているよ。
1人分を8こにしたら
9人いるから、全部のあめの数は8×9=72こになるよね。
→81こにならないから、まちがっているよ。
でもだんだん近づいてきたね。
1人分を9こにしたら
9人いるから、全部のあめの数は9×9=81こになるよね。
→とうとう81こになったね。
だから、81このあめを9人でわけると、1人分は9こが答えだよ。
いま、ひたすら考えたことは
下の▢にあてはまる数は何が入るかな?と予想したことだよ。
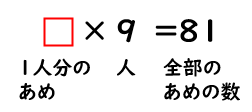
つまり、「9に、何をかけると81になるだろう?」ということを考えるんだね。
かけ算の九九をつかって、▢にじゅん番に数字を入れてたしかめていくと、9にかけると81になるのは、「9」ということがわかったね。
だから、▢にあてはまる数は「9」が答えだね。
わり算のやり方
わり算を計算するときは、「わる数」に何をかけると「わられる数」になるかを考えよう。
例:81÷9のばあい、「わる数(9)」に何をかけると「わられる数(81)」になるかを、九九で考える。

「わる数(9)」に、9をかけると「わられる数(81)」になるので、答えは「9」。
81÷9=9
もう1つ問題をときながら、かくにんしよう。
あめが56こあるとき、7人でわけると1人分は何こになりますか。
わり算の式であらわすと、
56÷7
だね。
さっそく、かけ算の九九をつかって、1人分のあめの数を予想してみるよ。
1人分を1こにすると
7人いるから、全部のあめの数は1×7=7こになるよね。
→56こにならないから、まちがっているよ。
1人分を2こにすると
7人いるから、全部のあめの数は2×7=14こになるよね。
→56こにならないから、まちがっているよ。
1人分を3こにすると
7人いるから、全部のあめの数は3×7=21こになるよね。
→56こにならないから、まちがっているよ。
1人分を4こにすると
7人いるから、全部のあめの数は4×7=28こになるよね。
→56こにならないから、まちがっているよ。
1人分を5こにすると
7人いるから、全部のあめの数は5×7=35こになるよね。
→56こにならないから、まちがっているよ。
1人分を6こにすると
7人いるから、全部のあめの数は6×7=42こになるよね。
→56こにならないから、まちがっているよ。
1人分を7こにすると
7人いるから、全部のあめの数は7×7=49こになるよね。
→56こにならないから、まちがっているよ。
でも、だいぶ近づいてきたね。
1人分を8こにすると
7人いるから、全部のあめの数は8×7=56こになるよね。
→56こになったから、1人分が8こが答え。
いま、ひたすら考えたことは
下の▢にあてはまる数は何が入るかなと予想したことだったよね。
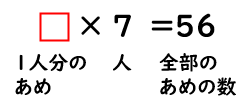
「7に、何をかけると56になるだろう?」ということを考えたんだったね。
かけ算の九九をつかって、▢にじゅん番に数字を入れてたしかめていくと、
7にかけると56になるのは、「8」ということがわかったね。
だから、▢にあてはまる数は「8」が答えだね。
56÷7を計算するには、「わる数(7)」に何をかけると「わられる数(56)」になるかを、九九で考えればいいんだね。

「わる数(7)」に、8をかけると「わられる数(56)」になるので、答えは「8」。
56÷7=8
わり算の練習問題
りんごが40こあります。8人でわけるとき、1人分は何こになりますか。
40÷8を計算すればいいから、次のようになるよ。

「わる数(8)」に何をかけると「わられる数(40)」になるかを、九九で考えればいいね。
▢にあてはまる数は「5」とわかるから、
1人分は「5こ」ともとめることができるよ。
45cmのひもがあります。9人でわけるとき、1人分は何cmになりますか。
45÷9を計算すればいいから、次のようになるよ。

▢にあてはまる数は「5」とわかるから、
1人分は「5cm」ともとめることができるよ。
「わり算(1人分の数をもとめる計算)」まとめ
「1人分の数」をもとめるには、「わり算」を使う。
わり算を表す記号は「÷(わる)」
例えば「30こを5人でわけたときの1人分」は「30÷5」という式で書く。
「30÷5」をもとめるには、「▢×5=30」の▢にあてはまる数をかけ算の九九でもとめる。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。


