「補集合」「全体の集合」わかりやすく解説(テスト対策ポイント)
補集合とは?補集合の記号は?高校数学A「補集合」について、全体集合と補集合の意味をイラストと漫画も使ってわかりやすく解説。数学A「補集合」
目次【本記事の内容】
- 1.補集合とは
- 2.全体の集合「U」とは
- 3.Aの補集合とは
- 4.まとめ
補集合とは
言葉が難しくて、よくピンとこないよ…
全体の集合「U」とは
ザックリいうと 「〇〇の中で」ということを表しているだけ!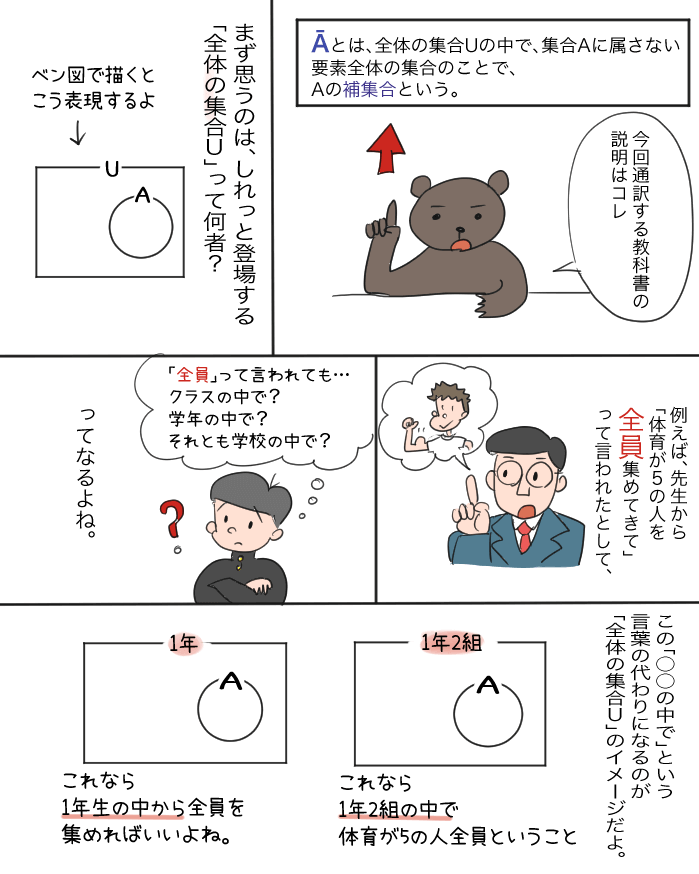 集合Aって、「△△なものを集めたAグループ」のことだったよね。
たとえば、上の説明で言えば「集合A」は「体育が5」のグループ、ということだね。
でも、この「体育が5」のグループを、どの範囲から探せばいいのかという情報って必要だよね。
「クラスの中から」なのか、「学校全体から」なのか、「東京の高校生全員から」なのか・・・
このことをハッキリさせるのが「全体の集合U」なんだ。
集合Aって、「△△なものを集めたAグループ」のことだったよね。
たとえば、上の説明で言えば「集合A」は「体育が5」のグループ、ということだね。
でも、この「体育が5」のグループを、どの範囲から探せばいいのかという情報って必要だよね。
「クラスの中から」なのか、「学校全体から」なのか、「東京の高校生全員から」なのか・・・
このことをハッキリさせるのが「全体の集合U」なんだ。
「Aの補集合」とは
ザックリいうと 「全体の集合U」の中で、「Aではない」グループのこと!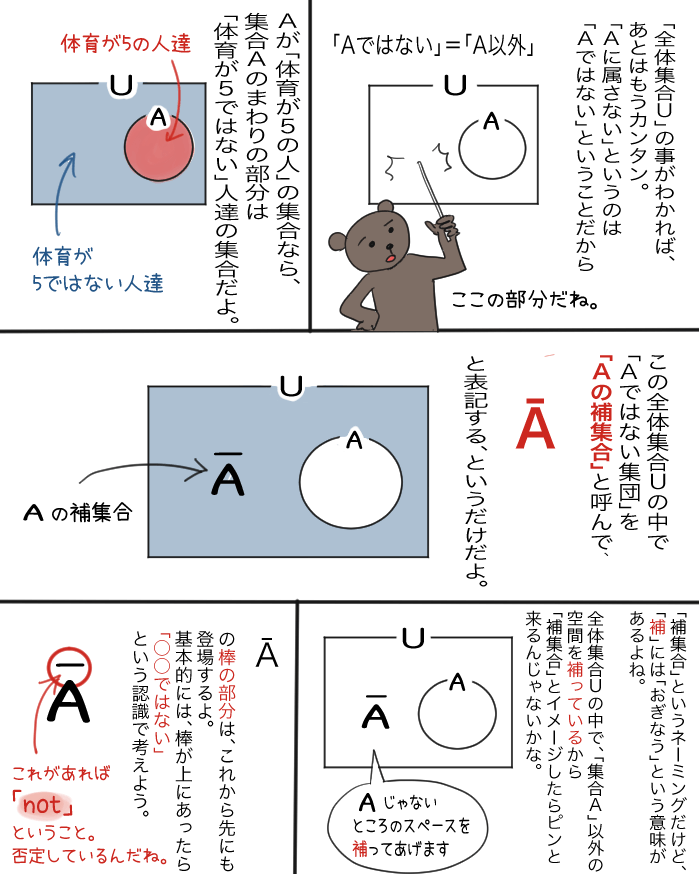
難しい言葉で書かれていると、ピンと来ないけれど、 「全体集合U」がどういうことか、「Aに属さない集合」が 何を指しているのか分かればそんなに難しいことではないよね。
補集合とは まとめ
まとめ
- 「全体の集合U」とは、ある集合(グループ)を選び出すときに、どの範囲から選べばいいのかをあらわしている。
- 「Aの補集合」とは、「全体の集合U」の中で、「Aではない」部分のこと。
- 「Aの補集合」のことを、「Ā」とあらわす。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。

-
-
たびたびの丁寧な回答ありがとうございます。
「補集合というのは、差集合の一種と考えることもできます」との説明で、少しもやもやがはれた気になりました。中1で計算の四則のところで数の種類の包含関係の図をみて、集合に興味をもったのですが、なんか疑問におもうたびに新しい言葉が出てきて奥が深くてきりがない感じにもさせられました。
でも先生のおかげで集合アレルギーにはならなくて済みそうです。



集合AとAの補集合Āと全体の集合Uの関係の表し方について教えてください。
① A+Ā=U
② AUĀ=U(和集合)
①、②ともどちらも正しいと思うのですがまちがっていませんか?