因数分解「たすきがけ」を早く簡単にする裏ワザの方法を解説

「たすきがけ」を使う因数分解、答えをもっと早く見つけて解く方法が知りたい！

高校数学Ⅰの因数分解の「たすき掛け」、候補の数字がたくさんあると、どれが正しい組み合わせかを見つけるまで何度も「たすき掛け」することになってしまって大変だよね。

そこで、このページでは「たすき掛け」での作業が格段に減る、いわば裏ワザを紹介するよ。
この方法を使えば、４つの数字を簡単な方法で見つけることが出来る んだ。

yumineko

いやいや、裏ワザよりもまずは高校数学の因数分解「たすき掛け」ってどんな公式？と思ったら先に因数分解の解説ページを確認しよう！

因数分解「たすきがけ」を早く簡単にする裏ワザの方法を解説のPDF（5枚）がダウンロードできます。

PDFを印刷して手書きで勉強したい方は以下のボタンからお進み下さい。

無料ダウンロードページへ

教科書では教えてくれない
「たすき掛け」の裏ワザとは？

では早速、「たすき掛け」で解く因数分解の問題を、裏ワザを使って解いてみるよ。

例題

2x²−5xy−3y²を因数分解せよ

【その1】
まずは「3つのポイント」を使って、
「3つの手がかり」をみつけよう！

今回注目するのは3つのポイント。

「たすき掛け」の公式
acx²＋(ad＋bc)x＋bd=(ax＋b)(cx＋d)
と問題を照らし合わせると、

ポイント①
ac=2なんだから、
aとｃをかけると「2」になる。

→この「2」は、手がかり①になるよ！

ポイント②
bd=-3ｙ²なんだから、
ｂとｄをかけると「-3ｙ²」になる

→この「-3ｙ²」が、手がかり②になるよ！

ここまでは、普通に「たすき掛け」で解く時と同じだね。
ここからが新しいポイント。

ポイント③

・和がｘの係数と同じ数字になって、
・積がｘ²の係数と、定数項をかけたものと同じ数字になる

２つの数字を探すんだ。

この問題のｘの係数は「-5ｙ」だよね。
ｘ²の係数と、定数項をかけたものは・・
「2」×「-3ｙ²」で、「-6ｙ²」。

つまり、和が「-5ｙ」で積が「-6ｙ²」になる２つの数字を探すんだ。

くまごろう

和が「-5ｙ」で、
積が「-6ｙ²」になる２つの数字だから、
「-6ｙ」と「ｙ」しかないね。
この「-6ｙ」と「ｙ」は、手がかり③になるよ！

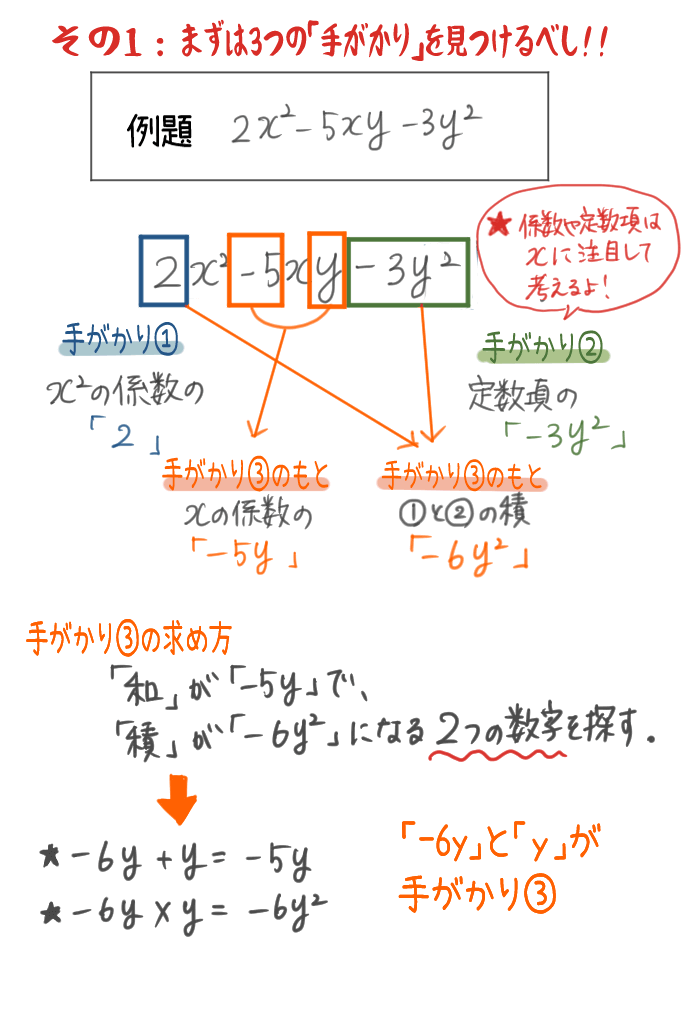
これで手がかりが3つそろって、4つの数字「2」「-3ｙ²」「-6ｙ」「ｙ」が見つかったね。

4つの数字を表に配置する

こうやって見つけた4つの数字を、下のような表の①、②、③にそれぞれ配置する よ。

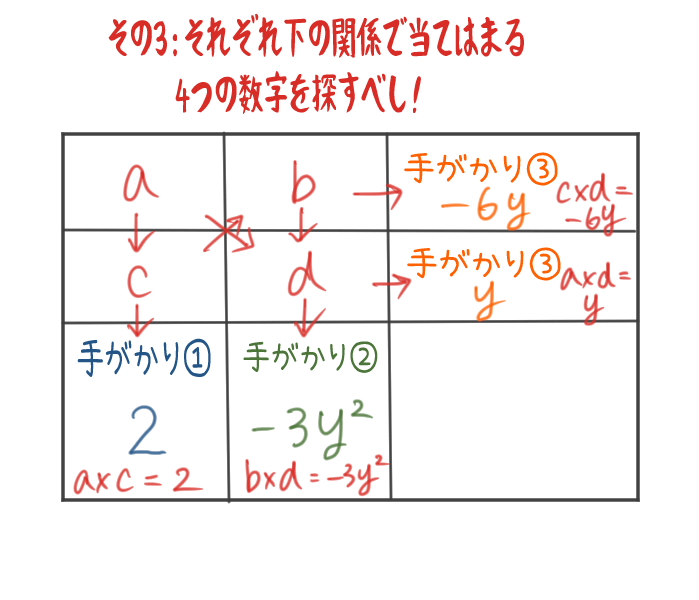
この表にはそれぞれ下の図の関係で
4つの答えの数字が当てはまる んだ。

くまごろう

普通のたすき掛けと決定的に違うところは、
「-6ｙ」と「ｙ」というように、右側部分の手がかりの答えももう分かってしまっているところ。
だから、考えられる答えの数字の組み合わせは１通りしかない んだ。

たろう

だから何度も候補を入れ替えたりする必要もなく、いっぺんに数字が揃うんだね。

関係を満たす4つの答えの数字をみつける

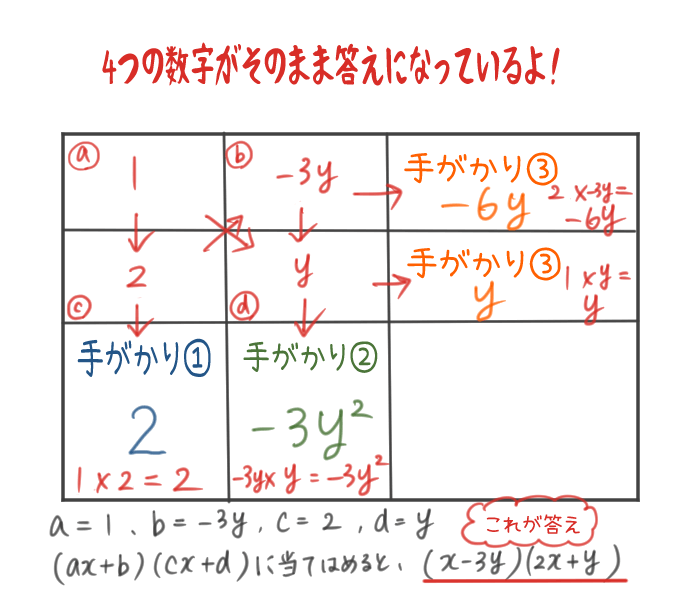
この関係を全て満たす数字の組み合わせは
下のとおり1つしかないよ。

これであっという間に
a=1
b=-3y
c=2
d=y
という４つの答えの数字が揃ったね！

答え：(x-3y)(2x+y)

因数分解「たすき掛けの裏ワザ」
まとめ

たすきがけを早くするコツまとめ

裏ワザを使うと、たすき掛けを何度もしなくてもいっぺんに答えの４つの答えの数字が見つけられる。
手順その① 3つのポイントから、4つの数字をみつける。
手順その② 4つの数字を表にする。
手順その③ 表の中の関係が全て満たされる4つの答えの数字をみつける。

yumineko

テストではいかに早く問題を解けるかがもちろん重要だよね。「たすき掛け」の因数分解が簡単にできるこの裏ワザをぜひ活用してね。

運営者情報

ゆみねこ
詳しいプロフィールを見る

青山学院大学教育学科卒業。TOEIC795点。２児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。