因数分解「たすきがけ」をわかりやすく解説(テスト対策ポイント)
高校数学Iで学習する、新しい因数分解の公式「たすきがけ」について、解き方の手順とポイントを解説するよ。
高校で習う新しい因数分解の公式「たすき掛け」とは?
 yumineko
yuminekoたすき掛けが必要になる因数分解の解き方パターンを見てみよう。
高校因数分解の解き方パターン③
「たすき掛けの公式を使って解く」
高校数学因数分解の解き方パターンは5つあったね。
その中の3つ目のパターンが「たすき掛け」の解き方なんだ。
 くまごろう
くまごろう例題
2x2−5xy−3y2 を因数分解せよ
 くまごろう
くまごろうこれまで学習したパターン①やパターン②の解き方は使えるかな?

パターン①の「くくりだし」は出来ないね。
パターン②の公式も・・・
当てはまるのがないや。
 くまごろう
くまごろうそれぞれの項の係数「2」と「-5」と「-3」では、くくりだしはできないし、
x2の前に係数があるから、今までに習った3つの因数分解の公式の形には当てはまらないから使えないよね。
 くまごろう
くまごろうたすきがけの公式とはどんな式?
(ax+b)(cx+d)

これも新しい展開の公式*
(ax+b)(cx+d)=acx2+(ad+bc)x+bd
を逆にしただけだね!
※展開の公式がピンと来ない
場合はここをチェック!
そう。
新しく増えた展開の公式も、
「xの前にそれぞれ異なる係数」があっても対応できるために加わった公式だったね。
因数分解でも同じこと。
「x2の前に係数があっても対応できるために加わった」というイメージでいいよ。
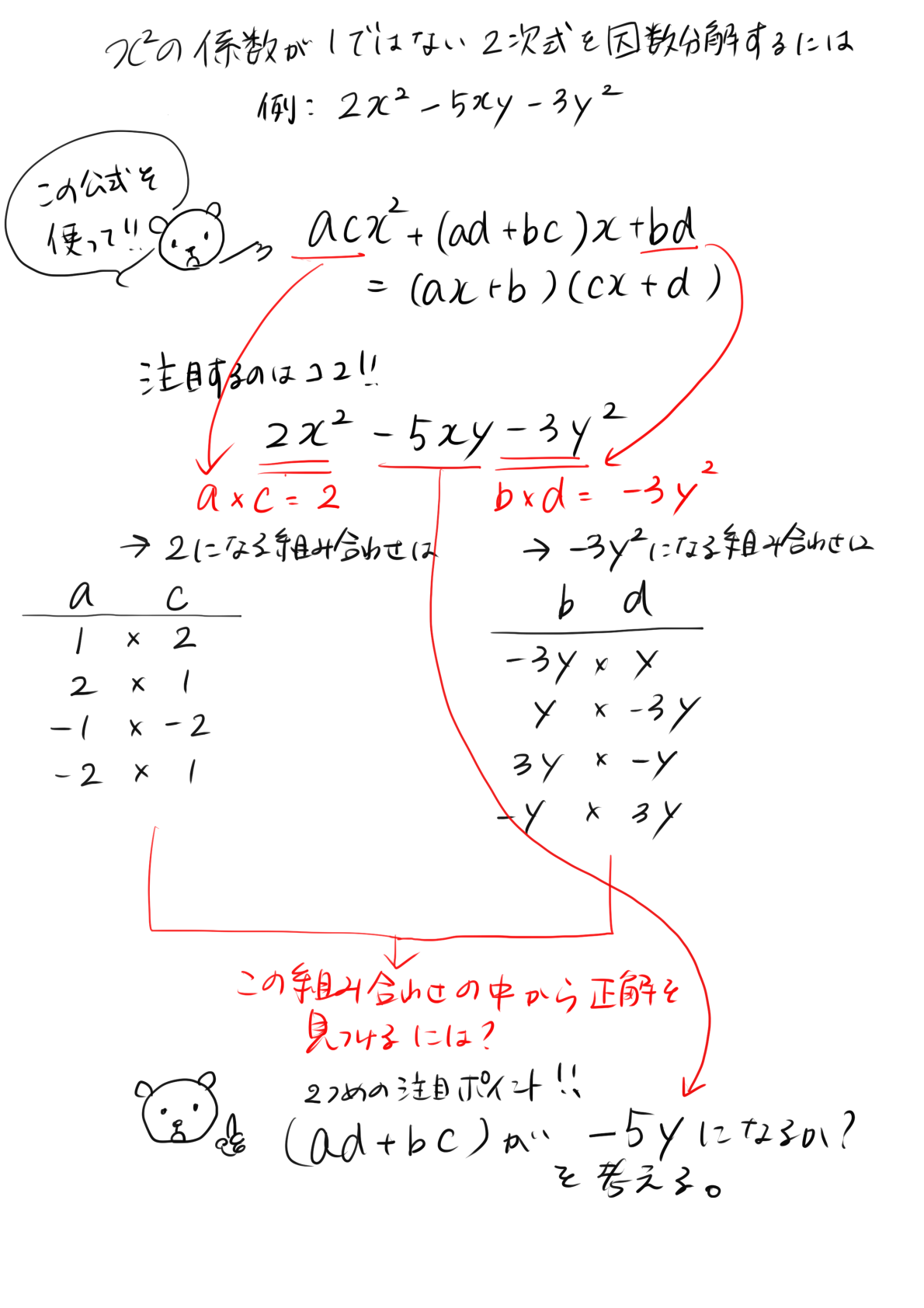
それでは、今回の問題を実際に公式に当てはめてみよう。
問題の式 2x2−5xy−3y2
公式 acx2+(ad+bc)x+bd
それぞれ対応する部分に注目すると、
acx2=2x2
(ad+bc)x=−5xy
bd=−3y2
だよね。
つまり、aとcをかけたものが
「2」になるということだし、
adとbcを足すと
「−5xy」になるということだし、
bとdをかけたものが
「−3y2」になるんだよね。
この条件にあてはまる
4つの数字
a と b と c と d
を見つければいいんだ。
どうやって4つの数字を見つけるの?

 くまごろう
くまごろうでも、
ヒントがあるのが分かるかな?
ヒント①
aとcをかけたものが「2」になる
 くまごろう
くまごろう「かけて「2」になる数字の組み合わせ」って何が考えられる?

1×2=2しかないかな。
うん、
1と2の組み合わせだね。
 くまごろう
くまごろうaとcは、「1と2」なんだよね。
どちらがどちらかはまだ分からないけどね。
少なくとも、
a=1で、c=2
それか、
a=2で、c=1
または
a=−1で、c=−2
a=−2で、c=−1
この4パターンだよね。
a=1、c=2
a=2、c=1
a=−1、c=−2
a=−2、c=−1
のどれかである。
同じことで、
ヒント②
bとdをかけたものが
「−3y2」になる。
かけると−3y2 になる
数字の組み合わせは
−yと3y
または
yと−3yだね。
b=−y、d=3y
b=y、d=−3y
b=3y、d=−y
b=−3y、d=y
この4パターンだね。
ある程度4つの数字の候補が
絞れてきたね。
最後に
ヒント③
adとbcを足すと
「−5xy」になる。
この3つめのヒントで
数字が決まるんだ。
足し引きした結果
−5になる、というのも
大体のパターンは考えられるよね。
(−2)+(−3)=−5
(−6)+(+1)=−5
−5になる組み合わせは他にもあるんじゃない?と思ってしまうところだけど、
ヒント①と②で分かったようにaもbもcもdも、候補は1から3の数字なんだ。
その数字を掛け合わせて出来るものを考えれば十分。
例えば、−7+2も−5になるけど、
−7がそもそもありえないよね。
(1、2、3を掛け合わせて7は出来ない)
これで候補が見つかったので、
いよいよ「たすき掛け」をしていくよ。
たすき掛けのやり方
たすきがけの手順
- ①a,b,c,dそれぞれの候補の数字を
決められた位置に置いていく - ②斜めにかける(これが「たすきがけ」)
- ③それぞれの答えの和をもとめる
- ④③の答えがxの係数の数字と一致すれば
終わり!
図で解説するよ。

早速、候補の数字のパターンの
ひとつを置いてみよう。
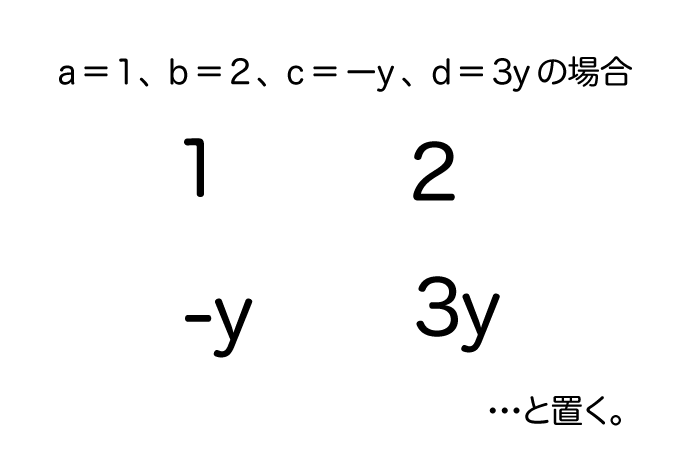
斜めに掛け合わせる
(たすきがけ)
求めた積の和を求める
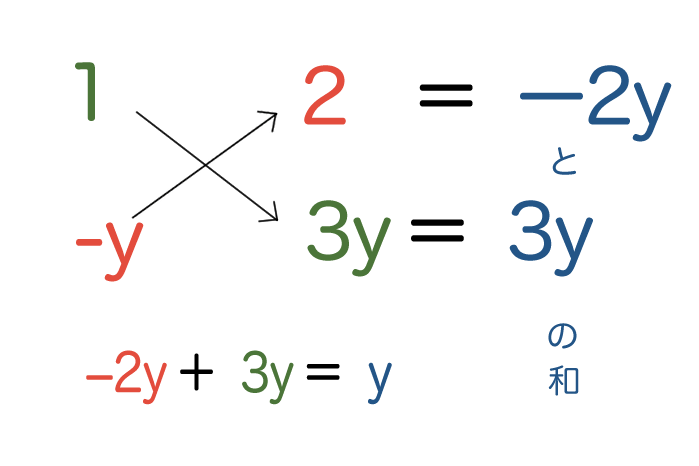
今回は、−2yと3yの和だから、
「y」になるね。
これは、問題の式 2x2−5xy−3y2の
xの係数「−5y」とは一致しない。
だから、この組み合わせではないんだ。
では、他の組み合わせを試すよ。
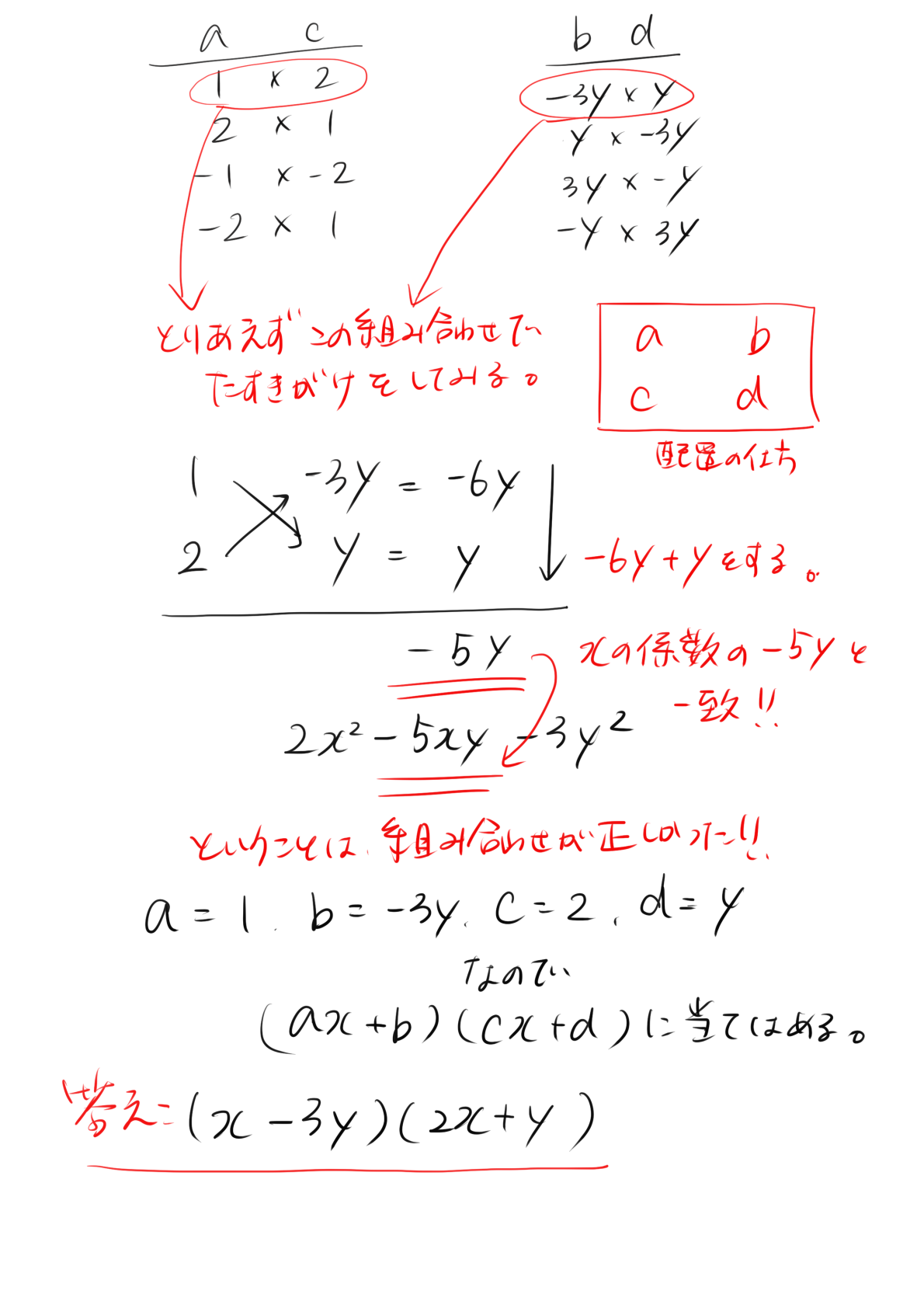
a=1 、b=-3y 、c=2 、d=y で試してみよう。
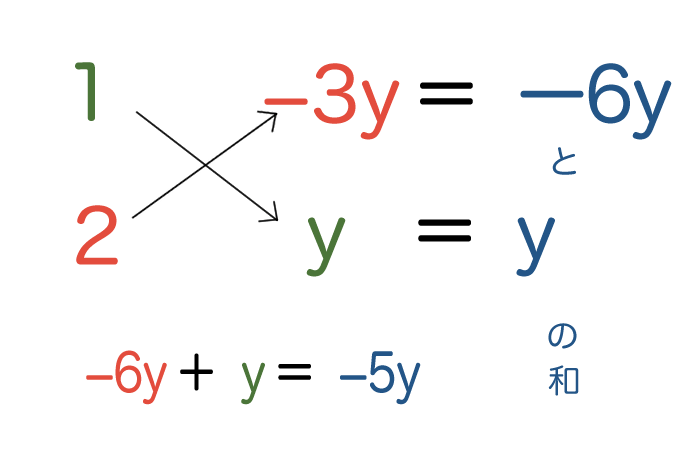
たすきがけした積の和が、xの係数と一致したね!
ということは、この組み合わせが正解なんだ。
あとは、公式のa、b、c、d
それぞれに
みつけた正解の組み合わせの数字を
当てはめれば、それが答えだよ。
公式
(ax+b)(cx+d)=acx2+(ad+bc)x+bd
の
(ax+b)(cx+d)に、
正解の組み合わせ
a=1、b=−3y、c=2、d=y
を当てはめて
(x-3y)(2x+y)
これが答えだね。
まとめ
 yumineko
yumineko運営者情報

yumineko
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。




