「命題と条件」とは?意味と真偽の見分け方をわかりやすく解説
「命題」とは?「条件」とは?
「命題と条件」とはどんな意味なのかをわかりやすく解説。命題の真偽の見分け方のコツを、集合(ベン図)を使って紹介するよ。
命題と条件とは
今回の学習では、「命題と条件」という範囲を勉強するんだけど、今まで勉強してきた数学とはだいぶ違う印象を受けると思うんだ。
数学を深く学んでいくと、論理的に話を組み立て、考え、表現することが必要になるんだ。今日はその第一歩だと思ってほしい。いよいよ高校数学も本格的になってきたなって感じがするね!
今回の話だけを聞くと「なんでそんなことを考える必要があるの?」って思うかもしれないけど、これはこの先の数学で必要なんだな、って思って読んでほしいな。
この単元は、「初めて学ぶ人」と「もっと先の数学を勉強していて、この単元の復習をする人」で、読んでほしい内容を分けて説明するよ。
「初めて学ぶ人」も、全部の文章に目を通してもらいたいけれど、「復習する人」のための内容は、深く考えすぎずにサラッと読み飛ばしてくれていいよ。この単元を初めて学ぶときは、あまりこだわり過ぎてしまうと、こんがらがっちゃうんだ。
だから、「へえ~、そんな風に考えるんだ」っていうくらいの理解でOK!
「復習する人」のための内容は、四角で囲っておくから参考にしてね!
命題とは
一般に、正しいか正しくないかが定まる文や式を命題という。
命題が正しいとき、その命題は真である、または成り立つという。また、命題が正しくないとき、その命題は偽である、
または成り立たないという。
正しいか正しくないかが定まらない分野式は命題ではない。
教科書の文章を読むと、命題っていうものは、「正しい」って決められるかどうかが大事なんだね。
曖昧なものや、人によって感じ方が違うようなものは命題とは言わないんだ。
いくつか例を見てみよう。
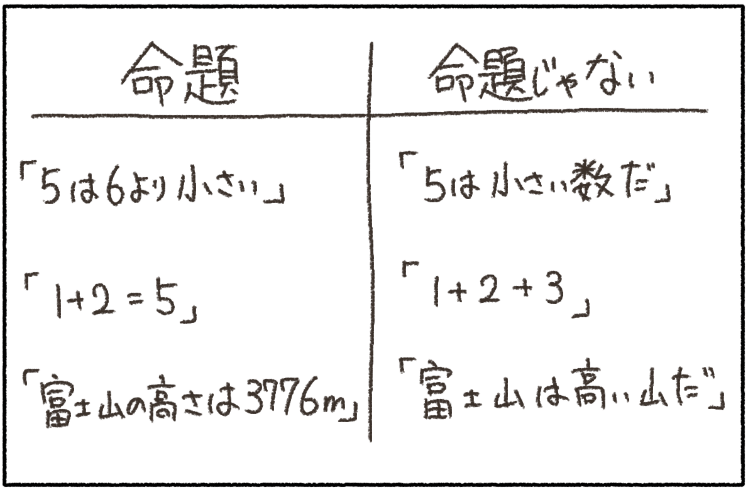
「富士山の高さは3776m」だなんて、数学っぽくなくても命題なの?とびっくりしてしまうよね。
命題は、「正しい」か「正しくない」かがハッキリするならOKなんだ。
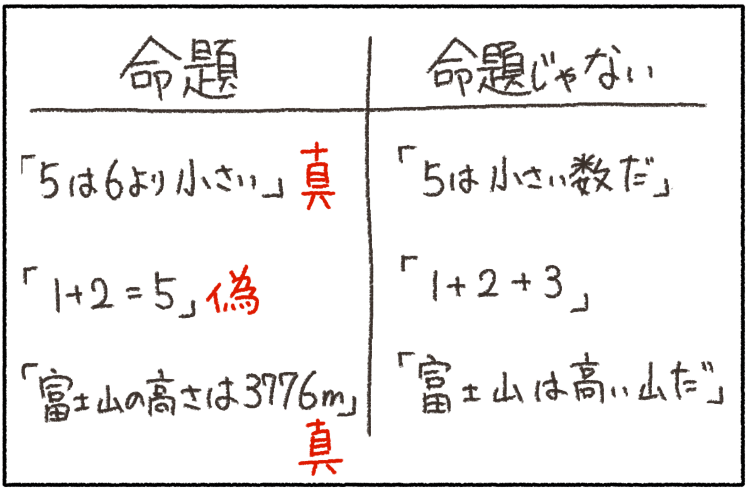
でも、ちょっと待って。「1+2=5」って、間違っているよね。
間違っているということは、「正しくない」と分かる式だという事だよね?
そう、正しくないと決まるから、「1+2=5」は命題で、そして「偽」ということなんだよ。
命題は、正しいときは真、正しくないときは偽、と言うんだよ。
条件とは
教科書の説明
変数を含む文や式で、その変数に値を代入した時に真偽が決まる文や式を条件という。
「正しい」か「正しくない」かが決まる文が命題って言うってことはわかったよ!
そこで、疑問なんだけど、「2x=6」みたいな式はどうなるのかな?
たしかに、「2x=6」は、「x=3」なら正しいけど、「x=1」だと正しくないよね。こういう時はどうするんだろう。

”「2x=6」は、「x=3」なら正しいけど、「x=1」だと正しくない”というように、xの値によって真偽が変わる文章は条件と言うんだ。
命題「\(p \Rightarrow q\)」
命題には、「〇〇ならば△△」という形になるものが多いんだよ。
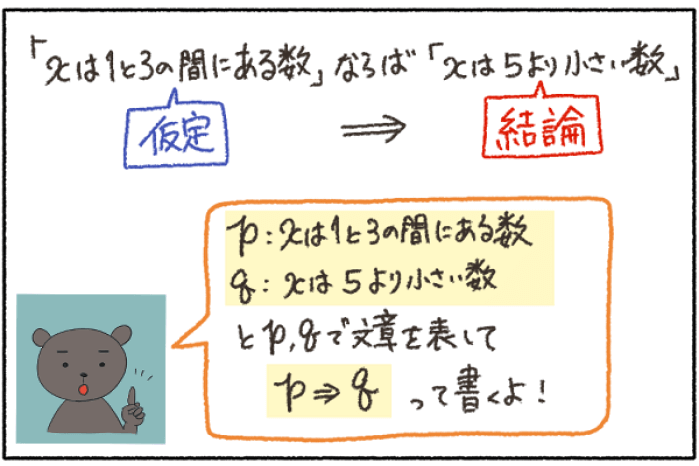
「xは1と3の間にある数」 ならば 「xは5より小さい数」
これは命題かな?
まず、真か偽か決められるか見てみよう。
「xは1と3の間にある数」
→(例)「2」や「2.5」
ならば
「xは5より小さい数」
→5より小さい数
1と3の間にある数なら、確実に5よりは小さいから、「真」だね。
真偽が決まったということは、これは命題と言えるってことだね。
こういう形の文章の時、「仮定」⇒「結論」というよ!
復習する人にポイント解説
ところで、\(p \Rightarrow q\)の文章をもう一度見返して欲しいんだけど、p、qはそれぞれ、「条件」であることが分かるかな?
仮定にあたる、「xは1と3の間にある数」だけを抜き出すと、xの値によって、真偽が変わるね。
だから、仮定だけに注目すると、それは「条件」であることが分かるし、同じように結論もまた「条件」になっている。
\(p \Rightarrow q\)の形の命題は、「ある条件」ならば「別の条件」という文や式が、真か偽かを考えているってことだね。
命題「\(p \Rightarrow q\)」と集合
さっきの命題を、数直線に書いてみてほしいんだ。
仮定を青、結論を赤にして書いてみるね。
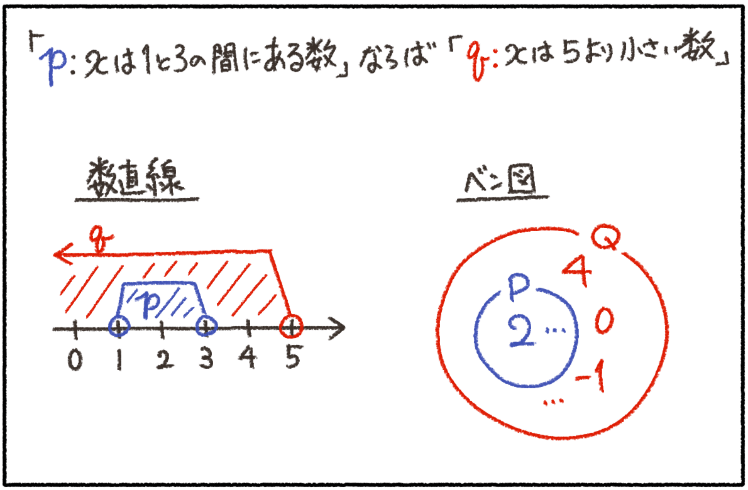
横にはベン図を書いてみたよ。何か気づくことはあるかな?
そう、数直線も、ベン図も、青が赤にすっぽり包まれているね。
こんな風に、仮定(青)が結論(赤)にすっぽり包まれている時、命題は真になるんだ!
命題と集合の考え方を説明するために、3つの例をあげてみよう。
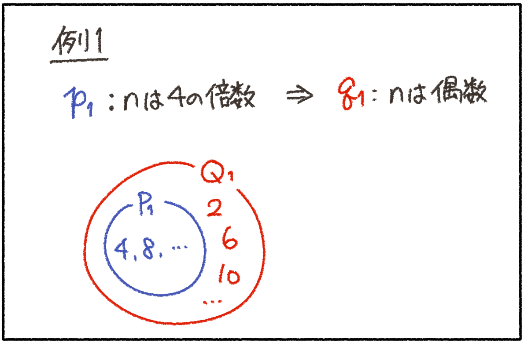

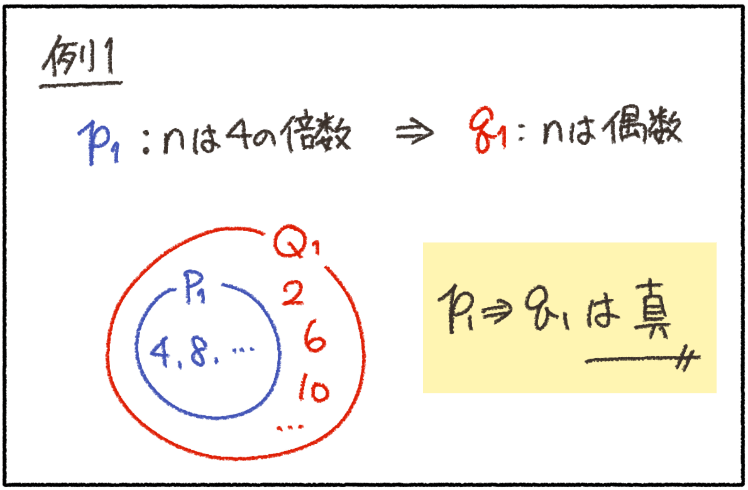
どれが真か、わかるかな?
仮定(青)がすっぽり包まれているのは、例1だから、例1は真だね!
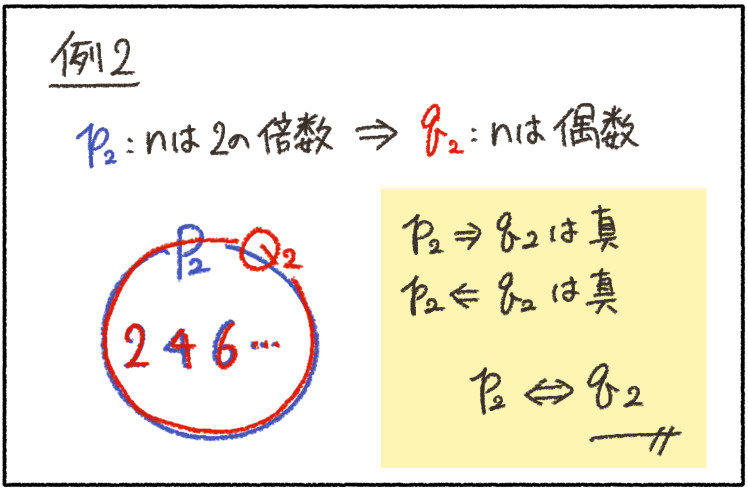
例2はどうかな?
重なっている…と言うか、例2の仮定と結論の輪っかは、まったく同じだよね。
でもこれも、すっぽり包まれていると言っていいんだ。
だから、これも真だね。
そして、例2のように、輪っかがまったく同じで重なる時、仮定と結論を結ぶ矢印である「⇒」が、
\(p \Rightarrow q\)、\(p \Leftarrow q\)、って感じで、両方の向きで真なんだ。こういう時は、まとめて「\(p \iff q\)」って書くよ。
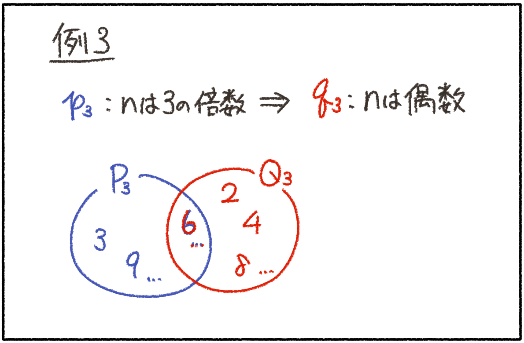
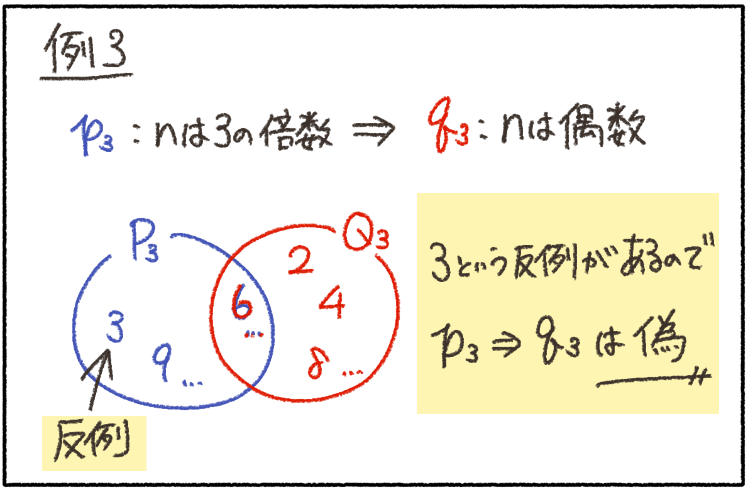
例3みたいに、包まれないで、はみ出している部分がある時はなんて言うのだろう?
こういう時、命題は偽なんだ。
「3の倍数」ならば「偶数」っていうのは、「正しくない(=ではない)」よね。
正しくないから命題は偽と言える。
命題が偽であることを示すためには、はみ出たところに入っているものをひとつ挙げればいいんだ。
つまり、「仮定には3があるから、この命題は偽です」という感じ。
この「3」のことを、反例というよ。
例3には3という反例があるので偽です!
なんだか裁判の「異議あり!」みたいでかっこいいね。
まとめ
「命題と条件」について、今回学習したことをまとめたよ。
「命題」とは
-
一般に、正しいか正しくないかが定まる文や式を「命題」という。→「正しい」か「正しくない」かがハッキリするならOK。
-
命題が正しいとき、その命題は「真」である、または「成り立つ」という。また、命題が正しくないとき、その命題は「偽」である、または「成り立たない」という。
-
正しいか正しくないかが定まらない文や式は命題ではない。
「条件」とは
-
変数を含む文や式で、その変数に値を代入した時に真偽が決まる文や式を「条件」という。
-
命題には、「〇〇ならば△△」という形になるものが多く、このような形の文章の時、「仮定」⇒「結論」という。
【ベン図での命題の真偽の見分け方】
-
仮定(青)が結論(赤)にすっぽり包まれている時、命題は真になる。
-
輪っかがまったく同じで重なる時、仮定と結論を結ぶ矢印である「⇒」は \(p \Rightarrow q\)、\(p \Leftarrow q\) というように、両方の向きで真である。このような時は、まとめて \(p \iff q\) と書く。
-
包まれないで、はみ出している部分がある時は命題は偽である。
-
命題が偽であることを示すためには、はみ出たところに入っているものをひとつ挙げればよい。この「はみ出たところに入っている」ものを「反例」という。
運営者情報

檜垣 由美子(ゆみねこ)
詳しいプロフィールを見る
青山学院大学教育学科卒業。TOEIC795点。2児の母。2019年の長女の高校受験時、訳あって塾には行かずに自宅学習のみで挑戦することになり、教科書をイチから一緒に読み直しながら勉強を見た結果、偏差値20上昇。志望校の特待生クラストップ10位内で合格を果たす。 ※サイト全体の運営実績についてはこちらにまとめています。




